Касательная к графику функции реферат

Обновлено: 04.07.2024

Чтобы разобраться с этой темой, нужно знать что такое производная.

Сейчас проверим, знаешь ли ты ее… 🙂

Найди приращение функции \( y=^>+2x+3\) при приращении аргумента, равном \( \Delta x\).

Должно получиться \( \Delta y=\Delta x\left( \Delta x+2x+2 \right)\).

А теперь найди производную функции \( y\left( x \right)=3^>\sqrt\) в точке \( <_>=\frac<<\pi >^>\).

Знаю, тема очень большая, но иначе нет смысла идти дальше…

А если ты справился, то в путь!

Уравнение касательной к графику функции — коротко о главном

Геометрический смысл производной

Производная функции в конкретной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или угловому коэффициенту этой касательной:

Уравнение касательной

Уравнение касательной к графику функции \( f\left( x \right)\) в точке \( _>\):

Алгоритм действий для нахождения уравнения касательной

Алгоритм	Пример: \( f\left( x \right)=^>-2x+3\), \( _>=3\)
1. Вычислим \( f\left( _> \right)\)	\( f\left( _> \right)=f\left( 3 \right)=^>-2\cdot 3+3=6\)
2. Найдем формулу производной функции \( ’\left( x \right)\)	\( ’\left( x \right)=<<\left( ^>-2x+3 \right)>^<\prime >>=2 -2\)
3. Вычислим \( ’\left( _> \right)\)	\( ’\left( _> \right)=’\left( 3 \right)=2\cdot 3-2=4\)
4. Подставим \( _>,\text< >f\left( _> \right)\) и \( ’\left( _> \right)\) в формулу уравнения касательной \( y=’\left( _> \right)\cdot \left( x-_> \right)+f\left( _> \right)\)	\( \beginy=’\left( _> \right)\cdot \left( x-_> \right)+f\left( _> \right)=\\\text< >=4\left( x-3 \right)+6=4 -12+6=\\\text< >=4 -6\end\)

Геометрический смысл производной

Рассмотрим график какой-то функции \( y=f\left( x \right)\):

Выберем на линии графика некую точку \( A\). Пусть ее абсцисса \( _>\), тогда ордината равна \( f\left( _> \right)\).

Затем выберем близкую к точке \( A\) точку \( B\) с абсциссой \( _>+\Delta x\); ее ордината – это \( f\left( _>+\Delta x \right)\):

Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).

Обозначим угол наклона прямой к оси \( Ox\) как \( \alpha \).

Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.

Какие значения может принимать угол \( \alpha \)?

Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – \( 180<>^\circ \), а минимально возможный – \( 0<>^\circ \).

Значит, \( \alpha \in \left[ 0<>^\circ ;180<>^\circ \right)\). Угол \( 180<>^\circ \) не включается, поскольку положение прямой в этом случае в точности совпадает с \( 0<>^\circ \), а логичнее выбирать меньший угол.

Возьмем на рисунке такую точку \( C\), чтобы прямая \( AC\) была параллельна оси абсцисс, а \( BC\) – ординат:

По рисунку видно, что \( AC=\Delta x\), а \( BC=\Delta f\).

Тогда отношение приращений:

(так как \( \angle C=90<>^\circ \), то \( \triangle ABC\) – прямоугольный).

Давай теперь уменьшать \( \Delta x\).

Тогда точка \( B\) будет приближаться к точке \( A\). Когда \( \Delta x\) станет бесконечно малым \( \left( \Delta x\to 0 \right)\), отношение \( \frac\) станет равно производной функции в точке \( _>\).

Что же при этом станет с секущей?

Точка \( B\) будет бесконечно близка к точке \( A\), так что их можно будет считать одной и той же точкой.

Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки \( A\), но этого достаточно).

Говорят, что при этом секущая занимает предельное положение.

Угол наклона секущей к оси \( \displaystyle Ox\) назовем \( \varphi \). Тогда получится, что производная

Производная равна тангенсу угла наклона касательной к графику функции в данной точке

Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:

За что отвечает коэффициент \( \displaystyle k\)? За наклон прямой. Он так и называется: угловой коэффициент.

Что это значит? А то, что равен он тангенсу угла между прямой и осью \( \displaystyle Ox\)!

То есть вот что получается:

Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?

Посмотрим: Теперь углы \( \alpha \) и \( \displaystyle \varphi \) тупые. А приращение функции \( \Delta f\) – отрицательное.

Снова рассмотрим \( \triangle ABC\): \( \angle B=180<>^\circ -\alpha \text< >\Rightarrow \text< >\ \angle B=-\ \alpha \).

Получаем: \( \frac=-\ \alpha \text< >\Rightarrow \text< >\frac=\ \alpha \), то есть все, как и в прошлый раз.

Снова устремим точку \( \displaystyle B\) к точке \( \displaystyle A\), и секущая \( \displaystyle AB\) примет предельное положение, то есть превратится в касательную к графику функции в точке \( \displaystyle A\).

Итак, сформулируем окончательно полученное правило:

Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:

Это и есть геометрический смысл производной.

Окей, все это интересно, но зачем оно нам? Вот пример:

На рисунке изображен график функции \( \displaystyle y=\mathsf\left( x \right)\) и касательная к нему в точке с абсциссой \( _>\).

Найдите значение производной функции \( \displaystyle \mathsf\left( x \right)\) в точке \( _>\).

Решение.

Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:

\( \displaystyle f’\left( x \right)=k=\ \varphi\).

Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.

На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!

Угол наклона касательной к оси \( \displaystyle Ox\) – это \( \displaystyle \angle BAC\). Найдем тангенс этого угла:

Таким образом, производная функции \( \displaystyle \mathsf\left( x \right)\) в точке \( _>\) равна \( \displaystyle 1,2\).

Ответ: \( \displaystyle 1,2\).

Теперь попробуй сам.

Еще статью на геометрический смысл производной ты найдешь здесь: «Геометрический смысл производной«.

Решим два примера

Пример 1. На рисунке изображен график функции \( \displaystyle y=\mathsf\left( x \right)\) и касательная к нему в точке с абсциссой \( _>\). Найдите значение производной функции \( \displaystyle \mathsf\left( x \right)\) в точке \( _>\);

Пример 2. На рисунке изображен график функции \( \displaystyle y=\mathsf\left( x \right)\) и касательная к нему в точке с абсциссой \( _>\). Найдите значение производной функции \( \displaystyle \mathsf\left( x \right)\) в точке \( _>\).

Решение примера №1

Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:

\( \displaystyle k=f’\left( x \right)=\ \beta\).

Достроим треугольник со стороной \( \displaystyle AC\), лежащей на касательной.

Угол наклона касательной – это угол, отмеченный зеленым на графике.

Он тупой \( \left( >90<>^\circ \right)\), поэтому его тангенс не получится вычислить так же, как в предыдущем примере (ведь в прямоугольном треугольнике не может быть тупого угла).

Касательной к графику функции y=f(x) в точке называют прямую, проходящую через точку , с отрезком которой практически сливается график функции при значениях х сколь угодно близких к . . Поясним это определение на примере. Покажем, что прямая y = x+1 является касательной к графику функции в точке (1; 2). Для этого покажем графики этих функций при приближении к точке касания (1; 2). Черным цветом показан график функции. , касательная прямая показана синей линией, точка касания изображена красной точкой. Каждый последующий рисунок является увеличенной областью предыдущего (эти области выделены красными квадратами).

Прикрепленные файлы: 1 файл

касательная к графику.docx

Определения и понятия.

Углом наклона прямой y=kx+b называют угол , отсчитываемый от положительного направления оси абсцисс до прямой y=kx+b в положительном направлении (то есть, против часовой стрелки).

На рисунке положительное направление оси абсцисс показано горизонтальной зеленой стрелочкой, положительное направление отсчета угла изображено зеленой дугой, прямая показана синей линией, а угол наклона прямой - красной дугой.

Угловым коэффициентом прямой y=kx+b на зывают числовой коэффициент k.

Угловой коэффициент прямой равен тангенсу угла наклона прямой, то есть, .

Угол наклона прямой равен нулю, когда прямая параллельна оси абсцисс. В этом случае нулю равен и угловой коэффициент, так как тангенс нуля есть ноль. Следовательно, уравнение прямой будет иметь вид y=b.
Когда угол наклона прямой y=kx+b является острым ( или ), то угловой коэффициент k является положительным числом (так как тангенс острого угла принимает положительные значения ) и указывает на возрастание графика прямой.
В случае, когда прямая располагается перпендикулярно оси абсцисс (параллельно оси ординат) и задается равенством x=c, где c - некоторое действительное число.
Когда угол наклона прямой y=kx+b является тупым ( или ), то угловой коэффициент k является отрицательным числом и указывает на убывание графика прямой.

Прямую AB, проведенную через две точки графика функции y=f(x), называют секущей. Другими словами, секущая – это прямая, проходящая через две точки графика функции.

На рисунке секущая прямая AB изображена синей линией, график функции y=f(x) - черной кривой, угол наклона секущей - красной дугой.

Если принимать во внимание, что угловой коэффициент прямой равен тангенсу угла наклона (об этом говорили выше), и тангенс угла в прямоугольном треугольнике A BC есть отношение противолежащего катета к прилежащему (это определение тангенса угла), то для нашей секущей будет справедлива серия равенств , где - абсциссы точек А и В, - соответствующие значения функции.

То есть, угловой коэффициент секущей определяется равенством или , а уравнение секущей записывается в виде или (при необходимости обращайтесь к разделу уравнение прямой с угловым коэффициентом, проходящей через заданную точку).

Секущая прямая разбивает график функции на три части: слева от точки А, от А до В и справа от точки В, хотя может иметь более чем две общих точки с графиком функции.

На рисунке ниже приведены три фактически разных секущих (точки А и В различны), но они совпадают и задаются одним уравнением.

Нам ни разу не встречались разговоры о секущей прямой для прямой. Но все же, если отталкиваться от определения, то прямая и ее секущая прямая совпадают.

В некоторых случаях секущая может иметь с графиком функции бесконечное число точек пересечения. Например, секущая, определяемая уравнением y=0, имеет бесконечное число общих точек с синусоидой.

Поясним это определение на примере. Покажем, что прямая y = x+1 является касательной к графику функции в точке (1; 2). Для этого покажем графики этих функций при приближении к точке касания (1; 2). Черным цветом показан график функции , касательная прямая показана синей линией, точка касания изображена красной точкой.

Каждый последующий рисунок является увеличенной областью предыдущего (эти области выделены красными квадратами).

Хорошо видно, что вблизи точки касания график функции практически сливается с касательной прямой y=x+1.

А сейчас перейдем к более значимому определению касательной.

Для этого покажем, что будет происходить с секущей АВ, если точку В бесконечно приближать к точке А.

Рисунок ниже иллюстрирует этот процесс.

Секущая АВ (показана синей пунктирной прямой) будет стремиться занять положение касательной прямой (показана синей сплошной линией), угол наклона секущей (показан красной прерывистой дугой) будет стремиться к углу наклона касательной (изображен красной сплошной дугой).

Таким образом, касательная к графику функции y=f(x) в точке А – это предельное положение секущей AB при .

Вот теперь можно переходить к оописанию геометрического смысла производной функции в точке.

К началу страницы

Геометрический смысл производной функции в точке.

Рассмотрим секущую АВ графика функции y=f(x) такую, что точки А и В имеют соответственно координаты и , где - приращение аргумента. Обозначим через приращение функции. Отметим все на чертеже:

Из прямоугольного треугольника АВС имеем . Так как по определению касательная – это предельное положение секущей, то .

Вспомним определение производной функции в точке: производной функции y=f(x) в точке называется предел отношения приращения функции к приращению аргумента при , обозначается .

Следовательно, , где - угловой коэффициент касательной.

Таким образом, существование производной функции y=f(x) в точке эквивалентно существованию касательной к графику функции y=f(x) в точке касания , причемугловой коэффициент касательной равен значению производной в точке , то есть .

Заключаем: геометрический смысл производной функции в точке состоит в существовании касательной к графику функции в этой точке.

К началу страницы

Уравнение касательной прямой.

Для записи уравнения любой прямой на плоскости достаточно знать ее угловой коэффициент и точку, через которую она проходит. Касательная прямая проходит через точку касания и ее угловой коэффициент для дифференцируемой функции равен значению производной в точке . То есть, из пункта геометрический смысл производной функции в точке мы можем взять все данные для записи уравнения касательной прямой.

Уравнение касательной к графику функции y = f(x) в точке имеет вид .

Мы подразумеваем, что существует конечное значение производной , в противном случае касательная прямая либо вертикальна (если и ), либо не существует (если ).

В зависимости от углового коэффициента , касательная может быть параллельна оси абсцисс ( ), параллельна оси ординат ( в этом случае уравнение касательной будет иметь вид ), возрастать ( ) или убывать ( ).

Самое время привести несколько примеров для пояснения.

Составить уравнение касательной к графику функции в точке (-1;-3) и определить угол наклона.

Функция определена для всех действительных чисел (при необходимости обращайтесь к статье область определения функции). Так как (-1;-3) – точка касания, то .

Находим производную (для этого может пригодиться материал статьидифференцирование функции, нахождение производной) и вычисляем ее значение в точке :

Так как значение производной в точке касания есть угловой коэффициент касательной, а он равен тангенсу угла наклона, то .

Следовательно, угол наклона касательной равен , а уравнение касательной прямой имеет вид

Черным цветом показан график исходной функции, касательная прямая изображена синей линией, точка касания - красной точкой. Рисунок справа представляет собой увеличенную область, обозначенную красным пунктирным квадратом на рисунке слева.

Выяснить, существует ли касательная к графику функции в точке (1; 1), если да, то составить ее уравнение и определить угол ее наклона.

Областью определения функции является все множество действительных чисел.

При производная не определена, но и , следовательно, в точке (1;1) существует вертикальная касательная, ее уравнение имеет вид x = 1, а угол наклона равен .

Найти все точки графика функции , в которых:
a) касательная не существует; b) касательная параллельна оси абсцисс; c) касательная параллельна прямой .

Как всегда начинаем с области определения функции. В нашем примере функция определена на всем множестве действительных чисел. Раскроем знак модуля, для этого рассмотрим два промежутка и :

При x=-2 производная не существует, так как односторонние пределы в этой точке не равны:

Таким образом, вычислив значение функции при x=-2, мы можем дать ответ на пункта): , касательная к графику функции не существует в точке (-2;-2).

b) Касательная параллельна оси абсцисс, если ее угловой коэффициент равен нулю (тангенс угла наклона равен нулю). Так как , то нам нужно найти все значения х, при которых производная функции обращается в ноль. Эти значения и будут абсциссами точек касания, в которых касательная параллельна оси Ox.

При решаем уравнение , а при - уравнение :

Осталось вычислить соответствующие значения функции:

Поэтому, - искомые точки графика функции.

График исходной функции изображен черной линией, красными точками отмечены найденные точки, в которых касательные параллельны оси абсцисс.

c) Если две прямые на плоскости параллельны, то их угловые коэффициенты равны (об этом написано в статье параллельные прямые, параллельность прямых). Исходя из этого утверждения, нам нужно найти все точки графика функции, в которых угловой коэффициент касательной равен восьми пятым. То есть, нам нужно решить уравнение . Таким образом, при решаем уравнение , а при - уравнение .

Дискриминант первого уравнения отрицателен, следовательно, оно не имеет действительных корней:

Второе уравнение имеет два действительных корня:

Находим соответствующие значения функции:

В точках касательные к графику функции параллельны прямой .

График функции изображен черной линией, красной линией показан график прямой , синими линиями показаны касательные к графику функции в точках .

Для тригонометрических функций в силу их периодичности, может существовать бесконечно много касательных прямых, имеющих один угол наклона (одинаковый угловой коэффициент).

Написать уравнения всех касательных к графику функции , которые перпендикулярны прямой .

Чтобы составить уравнение касательной к графику функции нам достаточно знать ее угловой коэффициент и координаты точки касания.

Угловой коэффициент касательных найдем из условия перпендикулярности прямых: произведение угловых коэффициентов перпендикулярных прямых равно минус единице, то есть . Так как по условию угловой коэффициент перпендикулярной прямой равен , то .

Приступим к нахождению координат точек касания. Для начала найдем абсциссы, затем вычислим соответствующие значения функции – это будут ординаты точек касания.

При описании геометрического смысла производной функции в точке мы отметили, что . Из этого равенства найдем абсциссы точек касания.

Мы пришли к тригонометрическому уравнению. Просим обратить на него внимание, так как позже мы его используем при вычислении ординат точек касания. Решаем его (при затруднениях обращайтесь к разделу решение тригонометрических уравнений):

Абсциссы точек касания найдены, вычислим соответствующие ординаты (здесь используем равенство, на которое мы просили обратить внимание чуть выше):

Таким образом, - все точки касания. Следовательно, искомые уравнения касательных имеют вид:

На рисунке черной кривой показан график исходной функции на отрезке [-10;10], синими линиями изображены касательные прямые. Хорошо видно, что они перпендикулярны красной прямой . Точки касания отмечены красными точками.

К началу страницы

Касательная к окружности, эллипсу, гиперболе, параболе.

До этого момента мы занимались нахождением уравнений касательных к графикам однозначных функций вида y = f(x) в различных точках. Канонические уравнения кривых второго порядка не являются однозначными функциями. Но окружность, эллипс, гиперболу и параболу мы можем представить комбинацией двух однозначных функций и уже после этого составлять уравнения касательных по известной схеме.

Касательная к окружности.

Окружность с центром в точке и радиусом R задается равенством .

Запишем это равенство в виде объединения двух функций:

Здесь первая функция соответствует верхней полуокружности, вторая - нижней.

Таким образом, чтобы составить уравнение касательной к окружности в точке , принадлежащей верхней (или нижней) полуокружности, мы находим уравнение касательной к графику функции (или ) в указанной точке.

Легко показать, что в точках окружности с координатами и касательные параллельны оси абсцисс и задаются уравнениями и соответственно (на рисунке ниже они показаны синими точками и синими прямыми), а в точках и - параллельны оси ординат и имеют уравнения и соответственно (на рисунке ниже они отмечены красными точками и красными прямыми).

Касательная к графику функции
Касательная
График дифференцируемой в точке х0 функции f вблизи х0 практически не отличается от отрезка касательной, а значит, он близок к отрезку секущейl, проходящей через точки(х0; f(х0)) и (х0 +?x;f (х0+?x)). Любая из таких секущих проходит через точку А(х0; f(х0)) графика(рис.1).

Для того чтобы однозначно задать прямую, проходящую через данную точку А, достаточно указать ее угловой коэффициент. Угловой коэффициент секущей при ? х>0 стремится к числу f/( х0) -угловой коэффициент касательной.
Касательная есть предельное положение секущей при ? х>0.

Если же функция не существует, то касательная либо не существует ( как у функции y= ¦x¦в точке (0;0) рис.2), либо она вертикальна ( как у графика y=3vx в точке(0;0) рис.3
Итак, существованию производной функции f в точке х0 эквивалентно существованию ( не вертикальной) касательной в точке (х0; f (х0)) графика при этом угловой коэффициент касательной равен f/(х0). В этом и состоит геометрический смысл производной.

Касательная к графику дифференцируемой в точке х0 функции f – это прямая, проходящая через точку(х0; f(х0)) и имеющая угловой коэффициент f/( х0).

Уравнение касательной
Выведем теперь уравнение касательной к графику функции f в точке А(х0; f(х0)).
Уравнение прямой с угловым коэффициентом f/(х0) имеет вид:
y = f/ (х0) x +b
Для вычисления b воспользуется тем, что касательная проходит через точку А:

f(х0) = f/ (х0)x0 + b , откуда b= f (х0) — f/ (х0) x0
значит, уравнение касательной таково:
у= f/ (х0) x — f/ (х0) x0 +f (х0)
или
y= f (х0)+ f/ (х0)(x-x0)

Метод интервалов.
На свойстве непрерывных функций, рассмотренном в этом пункте ( его полное доказательство приводится в курсах математического анализа), основан метод решения неравенств с одной переменной(метод интервалов). Опишем его.
Пусть функция f непрерывна на интервале Iи обращается в нуль в конечном числе точек этого интервала. По сформулированному выше свойству непрерывных функций этими точками Iразбирается на интервалы. В каждом из которых непрерывная функция f сохраняет постоянный знак. Чтобы определить этот знак , достаточно вычислить значение функции f в какой –либо одной точке из каждого такого интервала.

Вы можете изучить и скачать доклад-презентацию на тему Касательная к графику функции. Презентация на заданную тему содержит 29 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

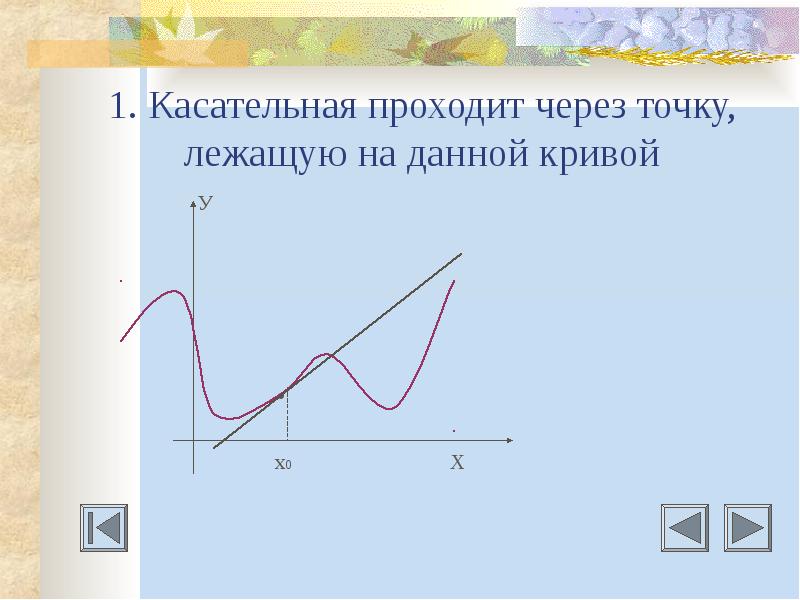
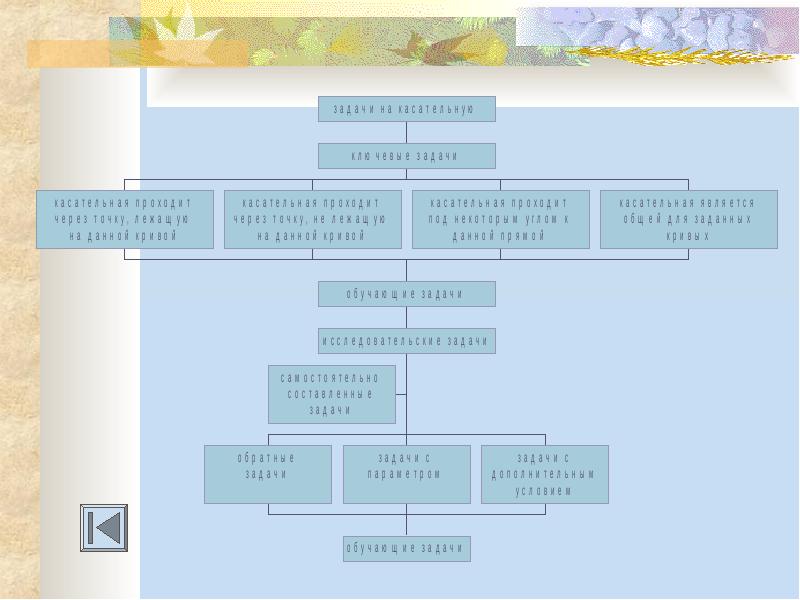
Содержание 1. Определение касательной к графику функции. 2. Уравнение касательной к графику функции в общем виде. 3. Алгоритм составления касательной к графику функции. 4. Условия параллельности и перпендикулярности двух прямых. 5. Касательная проходит через точку, лежащую на данной прямой. 6. Касательная проходит через точку, не лежащую на данной прямой. 7. Касательная проходит под некоторым углом к данной прямой. 8. Касательная является общей для двух кривых. 9. Является ли данная прямая касательной к графику функции у=f(x)?

Определение касательной к графику функции у=f(х) Пусть дана некоторая кривая и точка Р на ней. Возьмем на этой кривой другую точку Р1 и проведем прямую через точки Р и Р1. Эту прямую называют секущей. Будем приближать точку Р1 к Р. Положение секущей РР1 будет меняться (стремиться к точки Р) предельное положение прямой РР1 и будет касательной к кривой в точке Р.

Алгоритм составления касательной к графику функции у=f(x) Обозначить буквой а абсциссу точки касания. Найти f(а). Найти f’(x) и f’(а). Подставить найденные числа а, f(а), f’(а) в общее уравнение касательной у=f(a)+f’(a)(x-a)

Условия параллельности и перпендикулярности двух прямых. Пусть даны две прямые: у1=k1x+b1 и у2=k2x+b2. Если k1= k2, то прямая у1 параллельна у2. Если k1k2=–1, то данные прямые взаимно перпендикулярны

Даны дифференцируемая функция у=f(х) и Даны дифференцируемая функция у=f(х) и 1) абсцисса точки касания; 2) ордината точки касания; 3) абсцисса точки касания задана как пересечение двух графиков функций; 4) абсцисса точки касания задана как корень данного уравнения.

Решение таких задач сводится: к последовательному отысканию f(a) и f’(a); решая уравнение f(a)=у0, находим а; находим точки пересечения двух графиков; решая уравнение f(x)=g(x); находим корень данного уравнения.

Ключевая задача 1. Составьте уравнение касательной к графику функции у=х2–2х–3 в точке с абсциссой х0=2. Ключевая задача 1. Составьте уравнение касательной к графику функции у=х2–2х–3 в точке с абсциссой х0=2. Решение. 1. Обозначим абсциссу точки касания а, тогда а=2. 2. Найдем f(a): f(a)=22–2·2–3, f(a)=-3. 3. Найдем f’ (x) и f’(a): f’(x)=2x–2, f’(a)=2. 4. Подставим найденные числа а, f(a), в общее уравнение касательной у=f(a)+f’(a)(x–a): у=-3+2(х–2), у=-3+2х–4, у=2х–7 – уравнение касательной. Ответ: у=2х –7.

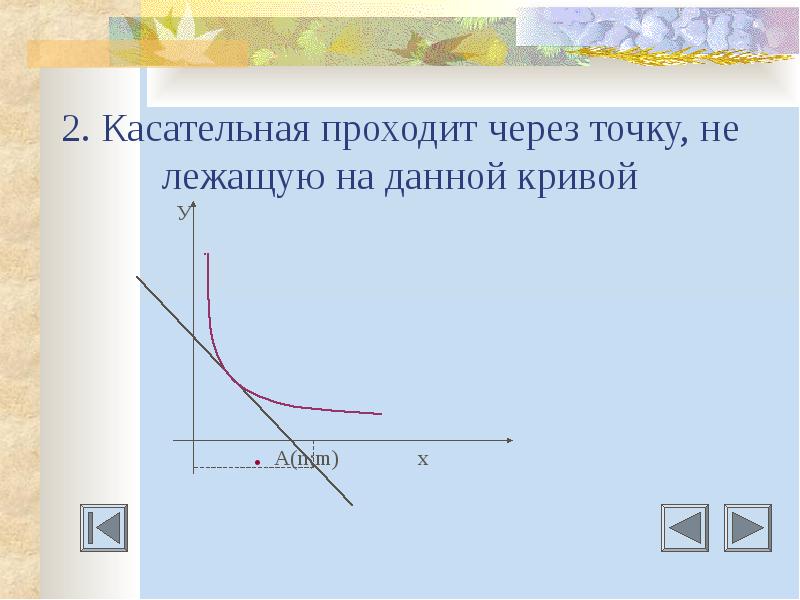
Даны дифференцируемая функция у=f(х) и Даны дифференцируемая функция у=f(х) и 1) точка А(n;m) через которую проходит касательная; 2) точка А(n;m) задана как пересечение двух графиков функций; 3) точка А(n;m) задана как корень системы уравнений.

Решение таких задач основывается на том, что координаты точки А(n;m) должны удовлетворять искомому уравнению касательной: решая уравнение m=f(a)+f’(a)(m-a) найдем а и, таким образом, приходим к задаче первого типа; находим точки пересечения двух графиков, решая уравнения f(x)=g(x) и у=g(х) или у=f(x); находим корень данной системы уравнений.

Ключевая задача 2. Напишите уравнение всех касательных к графику функции Ключевая задача 2. Напишите уравнение всех касательных к графику функции у = х2 +4х+6 проходящих через точку М(-3;-1). Решение. 1. Точка М(-3;-1) не является точкой касания, так как f(-3)=3. 2. а – абсцисса точки касания. 3. Найдем f(a): f(a) = a 2+4a+6. 4. Найдем f’(x) и f’(a): f’(x)=2x+4, f’(a)=2a+4. 5. Подставим числа а, f(a), в общее уравнение касательной у= f(a)+ f’(a)(x–a): y=a2+4a+6+(2a+4)(x–a) – уравнение касательной. Так как касательная проходит через точку М(-3;-1), то -1=a2+4a+6+(2a+4)(-3–a), a2+6a+5=0, a=-5 или a=-1. Если a=-5, то y=-6x–19 – уравнение касательной. Если a=-1, y=2x+5 – уравнение касательной. Ответ: y=-6x–19, y=2x+5.

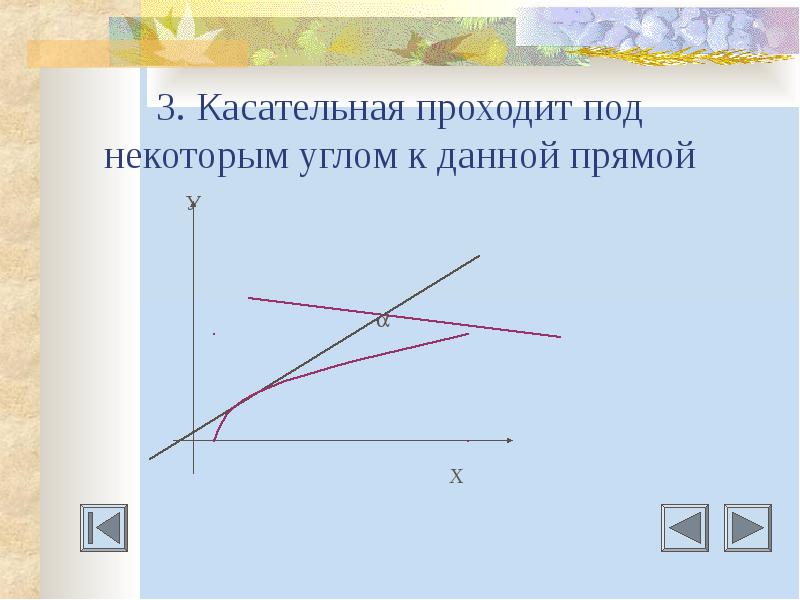
Даны дифференцируемая функция у=f(х) и Даны дифференцируемая функция у=f(х) и 1) значение производной в точке касания f’(а); 2) указан угловой коэффициент касательной; 3) задан угол, между касательной к графику функции и данной прямой.

Ключевая задача 3. Напишите уравнения всех касательных к графику функции у=х2–2х–8, параллельных прямой у=-4х–4. Ключевая задача 3. Напишите уравнения всех касательных к графику функции у=х2–2х–8, параллельных прямой у=-4х–4. Решение. 1. Обозначим абсциссу точки касания а. 2. Найдем f(a): f(a)=a2–2a–8. 3. Найдем f’(x) и f’(a): f’(x)=2x–2, f’(a)=2a–2. Но, с другой стороны, f’(a)= - 4 (условие параллельности). Решив уравнение 2a–2= - 4, получим a= - 1, f(a)= - 5. Подставим найденные числа а, f(a), в общее уравнение касательной у=f(a)+f’(a)(x-a): y=-5–4(x+1), y= - 4x–9 – уравнение касательной. Ответ: y= - 4x–9.

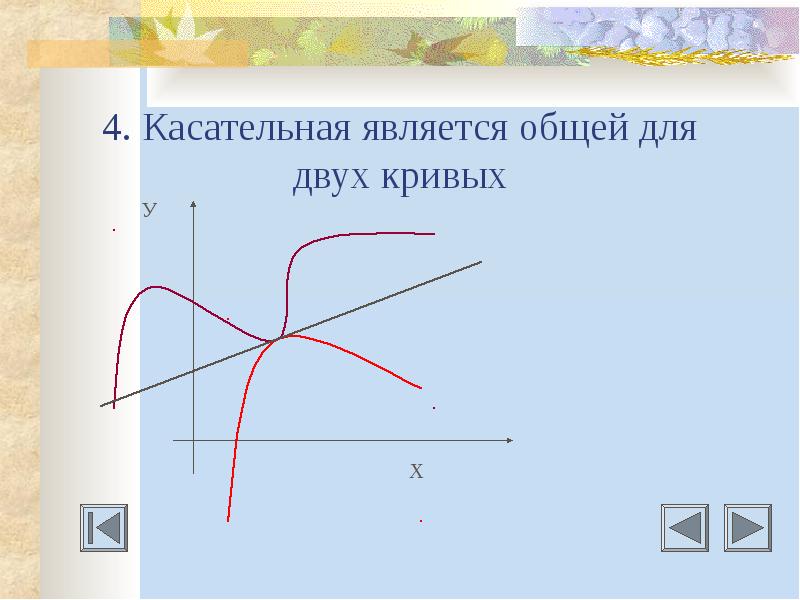
Даны дифференцируемые функция у=f(х) и y=g(x). Нужно найти уравнения общих касательных к графику этих функций. Даны дифференцируемые функция у=f(х) и y=g(x). Нужно найти уравнения общих касательных к графику этих функций.

1 способ. 1 способ. Такие задачи можно решать с помощью необходимого и достаточного признака того, что прямая у=kх+b является касательной к графику функции у=f(х) и у=g(х). Тогда задача сводится к решению системы: f(m)=km+b, g(n)=kn+b, f’(m)=k, g’(n)=k, где (m;f(m)) и (n;g(n)) – точки касания искомой прямой с графиками функций у=f(х) и у=g(х) соответственно. Решив систему, получим возможные значения k и b и запишем уравнения общих касательных в виде у=kх+b.

2 способ. 2 способ. 1) Находим уравнение касательной к графику функции у=f(х) в точке с абсциссой а. 2) Находим уравнение касательной к графику функции у=g(х) в точке с абсциссой а. 3) Полученные прямые должны совпадать, т. е. решаем систему: k1=k2, b1=b2.

Ключевая задача 4. Напишите уравнения всех общих касательных к графикам функций у=х2+х+1 и. у=0,5(х2+3). Ключевая задача 4. Напишите уравнения всех общих касательных к графикам функций у=х2+х+1 и. у=0,5(х2+3). Решение. I 1. а – абсцисса точки касания графика функции у=х2+х+1 2. Найдем f(a): f(a) =a2+а+1. 3. Найдем f’(x) и f’(a): f’(x)=2x+1, f”(a)=2a+1. 4. Подставим а, f(a), в общее уравнение касательной у=f(a)+ f’(a)(x–a): y=a2+а+1+(2a+1)(x–a), y=(2a+1)x–a2+1 – уравнение касательной. II. 1. с – абсцисса точки касания графика функции у=0,5(х2 +3). 2. Найдем f(c): f(c)=0,5c2 +1,5. 3. Найдем f’(x) и f’(c): f’(x)=х, f’(c)=c. 4. Подставим а, f(a), в общее уравнение касательной у=f(a)+ f’(a)(x–a): y=0,5c2+1,5+c(x–c), y=cx–0,5c2+1,5 – уравнение касательной. Так как касательная общая, то 2a+1=c, c=1, с=-3 –a2+1= –0,5c2+1,5 a=0; или а=-2 Итак, y=x+1 и y=-3x–3 общие касательные. Ответ: y=x+1 и y=–3x–3.

Является ли данная прямая касательной к графику функции у=f(x)? Даны дифференцируемая функция у=f(х) и уравнение прямой у=kх+b. Выясните, является ли данная прямая касательной к графику функции у=f(x).

1 способ. 1 способ. Если у=kх+b – уравнение к графику функции в точке с абсциссой а, то f’(а)=k. Решив это уравнение, находим а и задача сводится к решению первого типа задач на касательную. Полученное уравнение сравнивается с данным уравнением прямой.

2 способ. 2 способ. Прямая у=kх+b является касательной к графику функции у=f(x) в том и только том случае, если существует такое значение а, при котором совпадают значения данных функций и значения их производных, т. е. Совместна система f(a)=ka+b, f’(a)=k.

Представим разработанную систему задач в виде схемы. Представим разработанную систему задач в виде схемы.

Чтобы правильно и рационально решать задачи, связанные с уравнением касательной, нужно четко понимать, что такое касательная, владеть техникой составления уравнения касательной к графику функции и представлять себе, для решения каких задач (в том числе и задач с параметрами) можно использовать метод касательной.

Опр. 1. Касательной к графику функции у = f ( x ) называется предельное положение секущей MN при (рис. 1).

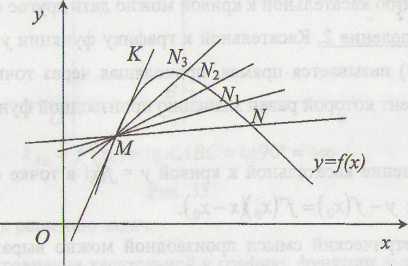
Касательная к кривой может иметь с ней несколько общих точек или пересекать ее. Можно дать и другое определение касательной к кривой.

Опр. 2. Касательной к графику функции у = f(x) в точке A 0 ( x 0 ; f ( x 0 )) называется прямая, проходящая через точку A 0 , угловой коэффициент которой равен значению производной функции у = f ( x ) в точке с абсциссой x 0 .

Уравнение касательной к кривой у = f ( x ) в точке с абсциссой х 0 имеет вид: .

Между понятием касательной и понятие производной имеется тесная связь. Геометрический смысл производной можно выразить так: если функция у = f ( x ) в точке х 0 имеет производную, то в точке с этой абсциссой определена касательная к графику функции , причем ее угловой коэффициент равен . Вывод: если в точке х 0 есть производная функции , то в точке с этой абсциссой есть касательная к графику функции и наоборот; если в точке х 0 нет производной функции , то в точке с этой абсциссой нет касательной к графику функции и наоборот.

Укажем случаи, когда функция не имеет в точке касательной, и, следовательно, не имеет и производной. Таких случаев три: угловая точка, точка возврата, узловая точка
(рис. 2 а, б, в). Особо отметим случай, когда в точке функция имеет бесконечную производную (рис. 2 г).

угловая точка точка возврата узловая точка

Рассмотрим решение некоторых задач.

Находим общие точки графиков, т. е. решаем уравнение f ( x ) = kx + b , а затем для каждого из его решений вычисляем . В тех случаях, когда = k , имеет место касание, в других — пересечение.

Решение. Записав условие касания получим

Решение. Пусть . Из условия следует, что должны выполняться равенство , где - возможная абсцисса точки касания. Имеем:

Решение. . Абсцисса интересующей нас точки касания удовлетворяет уравнению . Имеем:

Таким образом, . Значит, - абсцисса точки касания. Чтобы найти ординату точки касания преобразуем выражение, задающее функцию:

Решение. Так как касательная должна быть параллельна прямой , то ее угловой коэффициент, равный у'(х 0 ), где х 0 — абсцисса точки касания, совпадает с угловым коэффициентом данной прямой, т. е. . Отсюда или . Далее составляем уравнение касательной для каждой точки.

Решение. Найдем критические точки заданной функции:

Так как, производная в точках и равна нулю, то касательные, проведенные к кривой в точках с этими абсциссами, параллельны оси . Найдем значения функций в этих точках.

Итак, расстояние d между касательными, параллельными оси , равно

С составлением уравнения касательной, параллельной данной прямой, связана задача о нахождении кратчайшего расстояния между графиком некоторой функции f ( x ) и прямой .

Решение. Убедившись, что графики не имеют общих точек (уравнение не имеет решений), запишем уравнение такой касательной к графику функции , которая параллельна прямой Уравнение касательной имеет вид касание происходит в точке Прямая у = х – 2 и парабола у = х 2 расположены по разные стороны от касательной. Таким образом, кратчайшее расстояние между параболой и прямой равно расстоянию от точки М до прямой .

Довольно сложной является задача составления уравнения всех касательных к графику функции у = f ( x ), проходящих через заданную точку М(х 0 ; у 0 ), вообще говоря, не лежащую на графике. Приведем алгоритм решения этой задачи.

1. Составляем уравнение касательной к графику функции у = f ( x ) в произвольной точке графика с абсциссой t :

Указание. Уравнение касательной в точке с абсциссой t имеет вид . Так как эта касательная проходит через точку (2; -2), то
, откуда .

Указание. Уравнение дает два решения: t 1 = 1, t 2 = 4. Таким образом, точки K 1 (1;1) и K 2 (4;2) являются точками касания.

Решение. Найдем производную функции . В любой точке, в которой функция определена, производная отрицательна. Но производная есть тангенс угла наклона касательной, а так как он отрицателен, то угол тупой.

Решение. Пусть тогда . Составим уравнение касательной:

Решение. Из условия следует, что должно выполнятся равенство где абсцисса точки касания. Значит, и связаны между собой равенством (1). Составим уравнение касательной к графику заданной функции в точке

Решение. В этой задаче, как и в предыдущих, речь идет о касательных к графику функции. Составлять уравнение касательной не надо, достаточно использовать геометрический смысл производной, то есть угловые коэффициенты касательных. Графиком данной функции является парабола с ветвями, направленными вверх, пересекающая ось о x в двух точках (случай а= 0 нас не устраивает): и учитываем, что х 2 >0 (рис. 3)

Касательные АМ и ВМ пересекаются под углом 60 о в точке М, лежащей на оси параболы, причем возможны два случая: либо , либо смежный угол равен 60 о . в первом случае угол между касательной АО и осью х равен 120 о , следовательно, угол коэффициента касательной равен tg 120 o , то есть равен Далее имеем: . Таким образом, получаем, что , то . Во втором случае , поэтому угол между касательной АО и остью ох равен 150 о . Значит, угловой коэффициент касательной равен tg 150 o , то есть он равен . Таким образом, получаем, что , то есть

Далингер, В.А. Начала математического анализа в задачах [Текст]: учебное пособие / В.А. Далингер. – Омск: Изд-во ГОУ ОМГПУ, 2009. – 312 с.

Основные термины (генерируются автоматически): график функции, касательная, уравнение касательной, прямая, решение, абсцисса, касание, график функций, кратчайшее расстояние, угловой коэффициент.

Касательная к графику функции реферат

Уравнение касательной к графику функции — коротко о главном

Геометрический смысл производной

Прикрепленные файлы: 1 файл

касательная к графику.docx

Похожие статьи

Метод построения касательной кривой при заходе шпинделя.

Некоторые пути изучения понятия производной в школьном курсе.

Пути снижения динамических нагрузок в кинематических парах.

Трещины в композите, армированном однонаправленными.

GeoGebra как средство решения стереометрических задач

Применение рабочих тетрадей при оценивании предметных.

Компетентностный подход при решении качественных.

Похожие статьи

Метод построения касательной кривой при заходе шпинделя.

Некоторые пути изучения понятия производной в школьном курсе.

Пути снижения динамических нагрузок в кинематических парах.

Трещины в композите, армированном однонаправленными.

GeoGebra как средство решения стереометрических задач

Применение рабочих тетрадей при оценивании предметных.

Компетентностный подход при решении качественных.