История возникновения дифференциального исчисления реферат
Обновлено: 07.07.2024
1. Предмет математики и основные периоды ее развития. Математика представляет собой один из самых важных фундаментальных наук. Слово "математика" произошло от греческого слова "матема", что означает знания. Возникла математика на первых же этапах человеческого развития в связи с практической деятельностью людей. С самых древних времен люди, производя различные работы, встречались с необходимостью выделения и образования тех или иных совокупностей объектов, участков земли, жилищных потребностей объектов, жилищных помещений.
Во-первых, во всех этих случаях нужно было устанавливать количественные оценки рассматриваемых множеств, измерять их площади и объемы, сравнивать, вычислять, преобразовывать. По определению, данному Ф.Энгельсом:
МАТЕМАТИКА – это наука изучает количественные отношения и пространственные формы реального мира.
2. Основные математические понятия, такие как число, геометрическая фигура, функция, производная, интеграл, случайное событие и его вероятность и т.д. За свою историю математика, которая развивалась в тесной связи с развитием производственной деятельностью людей и общественной культуры, превратилась в стройную дедуктивную науку, представленную как мощный аппарат для изучения окружающего нас мира.
Академик А.Н. Калинов выделил четыре основных развития в истории математики.
Первый – период зарождения математики, начало которого лежит и теряется в глубинах тысячелетий истории человечества и продолжается до VI – V веков до нашей эры. В этом периоде создается арифметика, а также зачатки геометрии. Математические сведения этого периода состоят в основном из свода правил решения различных практических задач.
Второй период – элементарной математики, т.е. математики, постоянных величин (VI – V вв. до н.э. – XVII в. н.э.). Уже в начале этого периода (около 300 лет до н.э.) Евклид создает теорию трех книг ("Начало Евклида" - первый из дошедших до нас больших теоретических исследований по математике), в которых, в частности изучается дедуктивным образом на базе система аксиомы вся элементарная геометрия. Изданной в IX веке сочинения ал-Хорезми "Кибат ал-Джарап ал-Мукабана" содержит общие приемы решения задач, сводящие к управлению первой и второй степени. В XV веке вместо громких выражений стали употреблять знаки + и -, знаки степеней, корней, скобки. В XVI веке Ф.Виет применяет буквы для обозначения данных и не известных величин. К середине XVII века в основном сложилась современная алгебраическая символика, и этим были созданы основы формального математического языка.
Третий период – период создания математики переменных величин (XVII век – середина XIX века). Начиная с XVII века, в связи с изучением количественного отношения в процессе их изменения, на первый план выносили понятия переменной величины и функции. В этом периоде в работах Р.Декарта на базе мирового исследования метода системных координат создается аналитическая геометрия. В ра ботах И.Ньютона и Г.В.Лейбница завершает создание дифференциального интегрального исчисления.
Четвертый период – современные математики. Его начало следует относить к двадцатым годам XIX века – этот период начинается с работ Э.Гаусса, в которых заложены идеи теории алгебраических структур, В.И.Лобачевского, который открыл первую неевклидовую геометрию – геометрию Лобачевского.
В последствии дальнейшего распространения получил аксиоматический метод, в новую фазу вступили работы по обоснованию математики, математической логики и математическому моделированию. Создание в середине прошлого века ЭВМ привело не только более к глубокому и широкому применению математики в других областях знания, в технических науках, в вопросах организации и управления производством, но и зарождению развития новых областей теоретических и прикладных математических функций. Проникновения методов современной математики и ЭВМ в другие наук и практику применяет на столько всеобщий и глубокий характер, что одно из способностей нынешнего этапа развития человеческой культуры считается процесс математизации знаний и компьютеризации всех сфер трудовой деятельности и жизни людей.
3. Понятие о математическом моделировании. При изучении количественных характеристик сложных объектов, процессов явлений, пользуются методом математического моделирования, который состоит в том, что рассматриваемые закономерности формируются на математическом языке и исследуются при помощи соответствующих математических средств. Математический модуль изучаемого объекта записывается при помощи математических символов и состоит из совокупности уравнений, неравенств, формул, алгоритмов программ (для ЭВМ), в состав которых входят переменные и постоянные величины, различные операции, функции, быть может, и их производные, и другие математические понятия. Приемами составления простейших математических моделей служит хорошо известный, из курса математики средней школы, прием решения задач при помощи уравнений и систем уравнений – полученное уравнение или система уравнений является математической моделью данной задачи. Это были примеры задач с единственным решением – детерминированных задач. Однако часто встречаются задачи, имеющие много решений. В таких случаях на практике возникает вопрос о нахождении такого решения, которое является наиболее подходящим для той или иной точки зрения. Такие решения называются оптимальными решениями.
Оптимальное решение определяется как решение, для которого некоторая функция называется целевой функцией, принимает при заданных ограничениях наибольшее и наименьшее значения. Целевую функцию составляют из условия задачи, и она выражает величину, которую нужно оптимизировать (т.е. максимизировать или минимизировать), - например, получаемую прибыль, расходы, ресурсы и т.п.
Оказывается, что широкий класс, в частности задачи управления, составляют задачи в математических моделях которых условия на переменных создают неравенство или равенство. Теория и методы решения таких задач составляет раздел математики, известный под названием "Математическое программирование".
Если ограничения и целевая функция является многочисленным первой степени (линейны), то такие задачи составляют раздел математического программирования.
Математические модели больших производных систем, как правило, имеют сложную структуру. В частности, в них количество переменных и неравенств или уравнений могут насчитывать несколько десятков и даже сотен степеней имеют довольно сложный вид. Такие задачи решаются в вычислительных центрах с использованием больших вычислительных машин.
Следуя А.Н.Тихонову, в процессе решения реальных задач методом математического моделирования вычисляем следующие пять этапов:
1. Построение качественной модели, т.е. рассматривание явлений, выделение основных факторов и установление закономерностей, которые имеют место в следующем явлении.
2. Построение математической модели, т.е. перевод на язык математических состояний, установленных качественных закономерностей явлений. На этом же этапе состояния целевая функция, т.е. такая числовая характеристика переменных, наибольшему или наименьшему значению которой соответствует лучшая ситуация с точки зрения предыдущего решения.
3. Решение получаемой задачи. В связи с тем, что часто математические модели являются довольно громадными, вычисления проводятся с помощью ЭВМ в вычислительных центрах.
4. Сопоставление результатов вычислений являются неудовлетворительными, то переходят ко второму циклу процесса моделирования, т.е. повторяют этапы 1, 2, 3 с должными уточнениями информации пока не будет достигнуто удовлетворительное соглашение с имеющимися данными о модулируемом объекте.
Математические методы необходимо применять при решении крупных задач, таких как: финансовые отношения, планирование народного хозяйства, использование атомной энергией в широких целях, создание больших воздушных и космических кораблей разного назначения, обеспечение длительной работы научных экспедиций в космосе и т.д.
Однако было бы ошибочно думать, что математические методы нужны только для решения крупных задач. При изучении наук в средней школе мы встречаемся с применениями математических методов и вычислений в решении конкретных различных задач. Подобные задачи встречаются в ежедневной работе технических специалистов, экономистов, технологов. Поэтому работникам народного хозяйства, в какой бы области они не трудились, необходимо владеть основными методами исследования и приемами вычисления, устным, письменным, и машинным счетам. Специалисты должны иметь полное представление о возможностях современной ЭВМ.
В средней школе мы ознакомились с основными теориями уравнений, их систем, векторов, дифференциального и интегрального исчислениями и их применениями в решении практических задач.
Цель изучения математики в средних специальных заведениях состоит в том, чтобы углубить знания по изученным разделам и ознакомиться с некоторыми новыми разделами математики (аналитической геометрией, теорией вероятности и др.), которые обогащают общую культуру, развивает логическое мышление, широко используется в математическом моделировании задач, с которыми встречается современный специалист в своей повседневной деятельности.
Типовой учебный план
Типовой учебный план – это документ, предназначенный для реализации государственных требований к минимуму содержания и уровня подготовки выпускных учебных заведений средне специального образования. Он определяет общий перечень дисциплин, и обязательные объемы времени для их реализации, виды и минимальную продолжительность произведенной практики, примерный перечень учебных кабинетов, лабораторий и мастерских. В учебном плане также предусматривается курсовое проектирование не более чем по трем дисциплинам во весь период обучения. Виды производственной практики и их продолжительность определяется в соответствии с типовой учебной практики по заданной специальности. График учебного процесса носит рекомендательный характер и может быть откорректирован учебным заведением при обязательном соблюдении продолжительности теоретического обучения, экзаменационных сессий, а также сроков проведения зимних и завершающих учебный год летних каникул (см. таблицу 1).
| № п/п | Наиме-нование уч. Дисцип-лины | Распределение по семестрам | Мин. кол-во конт. работ | Количество часов | 2к | 4к | ||||||||
| Экзамен | Зачет | Курсовая | Всего | Теоретические занятия | Практические и семинарские занятия | Лабораторные занятия | Курсовой проект | 18нд | 12нд | 13нд | 13нд | |||
| 1. Цикл общеобразовательных | ||||||||||||||
| 1 | Высшая математика | 7 | 7 | 1 | 91 | 35 | 13 | 13 | 30 | 91 | ||||
Из учебного плана видно, что на предмет "Высшая математика" всего отводится 91 час. Из них 35 – теоретических, 13 – практических, 13 часов отводится на лабораторные занятия и 30 часов отведено на курсовой проект. Минимальное количество контрольных работ составляет 1 работа. Зачета нет. Курсовой проект сдается в 7 семестре. Экзамен проводится в 7 семестре. Предмет "Высшая математика" изучается на 3 курсе. В 7 семестре обучения 13 недель, в неделю по 7 часов: 13*7=91 час. Предмет полностью изучается на 3 курсе в 7 семестре.
История и важные этапы развития теории дифференциальных уравнений. Дифференциальное исчисление, созданное Лейбницем и Ньютоном. Доказательство неразрешимости алгебраических уравнений в радикалах. Простейшие дифференциальные уравнения первого порядка.
| Рубрика | Математика |
| Вид | доклад |
| Язык | русский |
| Дата добавления | 19.02.2016 |
| Размер файла | 21,9 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Историческая справка
на тему: Дифференциальные уравнения
Работу принял преподаватель: Беспалова С.П.
Работу выполнил студент группы 14А: Михеев А.В.
Дифференциальное уравнение - уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или все, кроме хотя бы одной производной, отсутствовать вовсе. Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, f'(x)=f(f(x)) не является дифференциальным уравнением.
Важнейшим вопросом для дифференциальных уравнений является существование и единственность их решения. Разрешение этого вопроса дают теоремы существования и единственности, указывающие необходимые и достаточные для этого условия. Для обыкновенных дифференциальных уравнений такие условия были сформулированы Липшицем (1864). Для уравнений в частных производных соответствующая теорема была доказана С. В. Ковалевской (1874).
Решения дифференциальных уравнений подразделяются на общие и частные решения. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных производных -- произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных). После определения вида указанных постоянных и неопределенных функций решения становятся частными.
Первоначально дифференциальные уравнения возникли из задач механики, в которых требовалось определить координаты тел, их скорости и ускорения, рассматриваемые как функции времени при различных воздействиях. К дифференциальным уравнениям приводили также некоторые рассмотренные в то время геометрические задачи.
Из огромного числа работ XVIII века по дифференциальным уравнениям выделяются работы Эйлера (1707--1783) и Лагранжа (1736--1813). В этих работах была прежде развита теория малых колебаний, а следовательно -- теория линейных систем дифференциальных уравнений; попутно возникли основные понятия линейной алгебры (собственные числа и векторы в n-мерном случае). Вслед за Ньютоном Лаплас и Лагранж, а позже Гаусс (1777--1855) развивают также методы теории возмущений.
Когда была доказана неразрешимость алгебраических уравнений в радикалах, Жозеф Лиувилль (1809--1882) построил аналогичную теорию для дифференциальных уравнений, установив невозможность решения ряда уравнений (в частности таких классических, как линейные уравнения второго порядка) в элементарных функциях и квадратуре. Позже Софус Ли (1842--1899), анализируя вопрос об интегрировании уравнений в квадратурах, пришёл к необходимости подробно исследовать группы диффеоморфизмов (получившие впоследствии имя групп Ли) -- так по теории дифференциальных уравнений возникла одна из самых плодотворных областей современной математики, дальнейшее развитие которой было тесно связано совсем с другими вопросами (алгебры Ли ещё раньше рассматривали Симеон-Дени Пуассон (1781--1840) и, особенно, Карл Густав Якоб Якоби (1804--1851)).
Порядком дифференциального уравнения называют наивысший порядок производной, входящей в данное уравнение.
Простейшие дифференциальные уравнения первого порядка -- класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.
Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:
где функции и определены и непрерывны в некоторой области .
К примеру можно представить закон радиоактивного распада частиц в виде уравнения:
которое означает, что число распадов ?dN, произошедшее за короткий интервал времени dt, пропорционально числу атомов N в образце.
Поиск решений обыкновенных дифференциальных уравнений привёл к установлению класса специальных функций -- часто встречающихся в приложениях функций, не выражающихся через известные элементарные функции. Их свойства были подробно изучены, составлены таблицы значений, определены взаимные связи и т. д.
Развитие теории дифференциальных уравнений позволило в ряде случаев отказаться от требования непрерывности исследуемых функций и ввести обобщённые решения дифференциальных уравнений.
Подобные документы
Задачи Коши для дифференциальных уравнений. График решения дифференциального уравнения I порядка. Уравнения с разделяющимися переменными и приводящиеся к однородному. Однородные и неоднородные линейные уравнения первого порядка. Уравнение Бернулли.
лекция [520,6 K], добавлен 18.08.2012
Решение дифференциальных уравнений с разделяющимися переменными, однородных, линейных уравнений первого порядка и уравнений допускающего понижение порядка. Введение функций в решение уравнений. Интегрирование заданных линейных неоднородных уравнений.
контрольная работа [92,7 K], добавлен 09.02.2012
Установление прямой зависимости между величинами при изучении явлений природы. Свойства дифференциальных уравнений. Уравнения высших порядков, приводящиеся к квадратурам. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
курсовая работа [209,4 K], добавлен 04.01.2016
Понятия и решения простейших дифференциальных уравнений и дифференциальных уравнений произвольного порядка, в том числе с постоянными аналитическими коэффициентами. Системы линейных уравнений. Асимптотическое поведение решений некоторых линейных систем.
дипломная работа [395,4 K], добавлен 10.06.2010
Дифференциальные уравнения Риккати. Общее решение линейного уравнения. Нахождение всех возможных решений дифференциального уравнения Бернулли. Решение уравнений с разделяющимися переменными. Общее и особое решения дифференциального уравнения Клеро.
курсовая работа [347,1 K], добавлен 26.01.2015
Порядок и процедура поиска решения дифференциального уравнения. Теорема существования и единственности решения задачи Коши. Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка, с разделяющими переменными.
лекция [744,1 K], добавлен 24.11.2010
История развития теории дифференциальных включений в математике. Элементы многозначного анализа. Операции над множествами. Понятия многозначного отображения. Дифференциальные включения и особенности их решения. Уравнения в паратингенциях и контингенциях.

Спецкурс, посвященный истории предмета призван помочь всем желающим пополнить и углубить свои знания в области математического анализа.
Факультативный курс
" История возникновения дифференциального исчисления"
Дифференциальное исчисление является одним из основных разделов начал математического анализа. Кроме того, материал по выбранной теме интересен с точки зрения истории, так как возникновение дифференциального исчисления оказало мощное влияние на дальнейшее развитие математики как науки.
Дифференциальное исчисление — раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций.
Спецкурс, посвященный истории предмета призван помочь всем желающим пополнить и углубить свои знания в области математического анализа. Данный курс состоит из 13 занятий.
В результате изучения данного курса учащиеся найдут ответ на проблемный вопрос: "Почему математика считается одним из главных инструментов познания действительности и изобретения нового" и смогут объяснить важную роль развития дифференциального исчисления в истории математики.
1)историю развития дифференциального исчисления;
2)имена, связанные с возникновением и развитием дифференциального исчисления.
1) Способствовать формированию и развитию у обучающихся:
учебно-познавательных, информационных, интеллектуальных и практических умений;
интереса к изучению математики;
коммуникативных навыков , которые способствуют развитию умений работать в группе, отстаивать свою точку зрения.
3) Обеспечить обучающимся условия для успешной поисково - исследовательской деятельности.
Для реализации программы факультатива используются лекции, самостоятельная работа с ресурсами сети интернет и библиотечным фондом , семинары.
Для получения информации об уровне усвоения курса данного факультатива учащимся предлагается:
выполнение индивидуальных заданий по каждой теме факультатива;
участие в конкурсной игре
В результате изучения курса обучающиеся
содержание периода развития дифференциального исчисления;
основополагающие математические идеи и понятия данного периода;
о роли персоналий в развитии математики;
объяснить важную роль развития дифференциального исчисления в истории математики;
рационально использовать полученные знания в практике;
работать со специальной историко-математической литературой и Internet-ресурсами.
ИСТОРИЧЕСКИЕ АСПЕКТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Формирование интегрального и дифференциального исчисления происходило на основе операций с бесконечно малыми (инфинитезимальными) величинами в процессе развития интегральных и дифференциальных методов и установления тесных связей между ними.
Источники возникновения и средства создания этих методов возникли независимо друг от друга на разных этапах развития математики. Долгое время эти методы применялись для решения двух разных групп задач.
Первая группа задач сводится к нахождению сумм бесконечно большого числа бесконечно малых слагаемых. Это - задачи об определении площадей, объёмов, работы, центров масс, моментов инерции и т.д.
Метод заключался в построении двух фигур U и V, между которыми одновременно находились фигуры А и В, такие, что площадь фигуры А известна, а площадь фигуры В неизвестна. Фигуры U и V подбирались так, чтобы разница площадей U–V была сколь угодно малой. Тогда методом от противного доказывалось, что площадь фигуры А равна площади фигуры В.
Значительный вклад в развитие интегральных методов сделал Архимед. Греки и до Архимеда умели находить площади многоугольников и круга, объём призмы и цилиндра, пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей и объёмов. Для этого он усовершенствовал и виртуозно применил метод вычерпывания Евдокса.
Таким образом, уже античная математика содержала элементы интегрального исчисления, однако ещё не в строгой форме, без чёткой теоретической основы.

Иоганн Кеплер (1572-1630)
Иоганн Кеплер, используя идеи Архимеда, обращался к интуитивным приемам и совсем не обосновывал их. Чтобы вычислить площадь какой-то фигуры, он разбивал её на бесконечное множество бесконечно малых элементов одной с ней размерности. Из этих элементов образовывал новую фигуру, площадь которой уже умел вычислять.
Основной опорой новой геометрии Б. Кавальери считал следующую теорему: Плоские фигуры относятся друг к другу, как все их линии, взятые по произвольной регуле, а пространственные тела - как все их плоскости, взятые по произвольной регуле.
Отсюда следует, что для нахождения отношения между двумя плоскими фигурами или пространственными телами достаточно найти отношения между всеми неделимыми обеих фигур или тел по какой-то регуле.
Б.Кавальери предложил много примеров успешного применения метода неделимых, как для известных тел, так и для новых (например, гиперболоида вращения). Он привёл пример парадокса, который может привести к ошибочным результатам из-за неудачного выбора неделимых сечений. Но понятного правила того, как избежать ошибок, он не дал.
В первой половине XVII века математики установили, что большое количество разнородных задач по геометрии и механике имеют общие пути решения и сводятся к квадратуре или кубатуре. Идеи, содержащие элементы определённого интегрирования, быстро распространялись среди математиков Западной Европы.
Их использовали и развивали Э. Торричелли, Паскаль, П. Ферма, Р. Декарт, Х. Гюйгенс, Д. Валлис, Н. Меркатор, И. Барроу. Однако при всей значимости результатов, интегральное исчисление как общего метода и универсального алгоритма ещё не было создано. Необходимо было выделить общие идеи, лежащие в основе решения многих конкретных задач.
Создание анализа бесконечно малых произошло во второй половине XVII века благодаря гениальным трудам Исаака Ньютона и Готфрида Вильгельма Лейбница.
Вторая группа задач охватывает задачи на движение и другие процессы. Для определения направления движения тела в некоторой точке его траектории нужно было ввести понятие касательной. Исследования кривых (в направлении которых летят снаряды, движутся планеты) ставили задачи на максимум и минимум.
Изучение движения вообще требовало понятия мгновенной скорости. Такого типа задачи ставились с древних времён, но решались тогда геометрическими и механическими способами, не связанными общей идеей. Так, Архимед исследовал, как построить касательную к кривой, как найти наибольшее значение произведения и т.д.
Только в XVII в. математики обнаружили, что все эти задачи можно решать единым методом, используя бесконечно малые величины. Этот метод получил развитие в трудах Р. Декарта, П. Ферма, Д. Грегори, Д. Валлиса, И. Барроу и других учёных. Развитие метода бесконечно малых величин привело к созданию дифференциального исчисления.
Наилучшие результаты в то время получили П. Ферма и И. Барроу. Выдающийся французский учёный Пьер Ферма (1601-1665) по сути умел находить производную произвольного многочлена от одной переменной. Пользуясь этим, он показал, как решать задачи на экстремум, в том числе - о вписывании в данный шар конуса наибольшего объёма, цилиндра наибольшей площади поверхности и т.п. Но само понятие производной он не выделил.

Исаак Барроу (1630-1677)
Применяя современные обозначения, доказанное им утверждение (теорема Барроу) можно записать так:
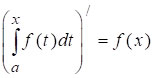
.
Таким образом была установлена взаимная обратимость операций дифференцирования и интегрирования. К доказательству этой зависимости И. Барроу подошёл двумя путями: кинематически и геометрически.
Теорема Барроу даёт возможность по результатам какого-либо дифференцирования или интегрирования найти результат обратной операции (т.е. установить первоначальную функцию). Используя этот результат, он решил ряд обратных задач на касательные.
С трудами И. Барроу ознакомились многие учёные, но они не поняли всеобщности и важности этой зависимости из-за громоздкой геометрической формулировки и пренебрежения аналитическими методами. Впоследствии учёные усовершенствовали формулировку и доказательство этой теоремы.
Это позволило теореме Барроу стать одной из важнейших в классическом математическом анализе. Именно она позволяет вычислять определённые интегралы (границы интегральных сумм) с помощью первоначальной функции.
ИСТОРИЧЕСКИЕ АСПЕКТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Формирование интегрального и дифференциального исчисления происходило на основе операций с бесконечно малыми (инфинитезимальными) величинами в процессе развития интегральных и дифференциальных методов и установления тесных связей между ними.
Источники возникновения и средства создания этих методов возникли независимо друг от друга на разных этапах развития математики. Долгое время эти методы применялись для решения двух разных групп задач.
Первая группа задач сводится к нахождению сумм бесконечно большого числа бесконечно малых слагаемых. Это - задачи об определении площадей, объёмов, работы, центров масс, моментов инерции и т.д.
Метод заключался в построении двух фигур U и V, между которыми одновременно находились фигуры А и В, такие, что площадь фигуры А известна, а площадь фигуры В неизвестна. Фигуры U и V подбирались так, чтобы разница площадей U–V была сколь угодно малой. Тогда методом от противного доказывалось, что площадь фигуры А равна площади фигуры В.
Значительный вклад в развитие интегральных методов сделал Архимед. Греки и до Архимеда умели находить площади многоугольников и круга, объём призмы и цилиндра, пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей и объёмов. Для этого он усовершенствовал и виртуозно применил метод вычерпывания Евдокса.
Таким образом, уже античная математика содержала элементы интегрального исчисления, однако ещё не в строгой форме, без чёткой теоретической основы.

Иоганн Кеплер (1572-1630)
Иоганн Кеплер, используя идеи Архимеда, обращался к интуитивным приемам и совсем не обосновывал их. Чтобы вычислить площадь какой-то фигуры, он разбивал её на бесконечное множество бесконечно малых элементов одной с ней размерности. Из этих элементов образовывал новую фигуру, площадь которой уже умел вычислять.
Основной опорой новой геометрии Б. Кавальери считал следующую теорему: Плоские фигуры относятся друг к другу, как все их линии, взятые по произвольной регуле, а пространственные тела - как все их плоскости, взятые по произвольной регуле.
Отсюда следует, что для нахождения отношения между двумя плоскими фигурами или пространственными телами достаточно найти отношения между всеми неделимыми обеих фигур или тел по какой-то регуле.
Б.Кавальери предложил много примеров успешного применения метода неделимых, как для известных тел, так и для новых (например, гиперболоида вращения). Он привёл пример парадокса, который может привести к ошибочным результатам из-за неудачного выбора неделимых сечений. Но понятного правила того, как избежать ошибок, он не дал.
В первой половине XVII века математики установили, что большое количество разнородных задач по геометрии и механике имеют общие пути решения и сводятся к квадратуре или кубатуре. Идеи, содержащие элементы определённого интегрирования, быстро распространялись среди математиков Западной Европы.
Их использовали и развивали Э. Торричелли, Паскаль, П. Ферма, Р. Декарт, Х. Гюйгенс, Д. Валлис, Н. Меркатор, И. Барроу. Однако при всей значимости результатов, интегральное исчисление как общего метода и универсального алгоритма ещё не было создано. Необходимо было выделить общие идеи, лежащие в основе решения многих конкретных задач.
Создание анализа бесконечно малых произошло во второй половине XVII века благодаря гениальным трудам Исаака Ньютона и Готфрида Вильгельма Лейбница.
Вторая группа задач охватывает задачи на движение и другие процессы. Для определения направления движения тела в некоторой точке его траектории нужно было ввести понятие касательной. Исследования кривых (в направлении которых летят снаряды, движутся планеты) ставили задачи на максимум и минимум.
Изучение движения вообще требовало понятия мгновенной скорости. Такого типа задачи ставились с древних времён, но решались тогда геометрическими и механическими способами, не связанными общей идеей. Так, Архимед исследовал, как построить касательную к кривой, как найти наибольшее значение произведения и т.д.
Только в XVII в. математики обнаружили, что все эти задачи можно решать единым методом, используя бесконечно малые величины. Этот метод получил развитие в трудах Р. Декарта, П. Ферма, Д. Грегори, Д. Валлиса, И. Барроу и других учёных. Развитие метода бесконечно малых величин привело к созданию дифференциального исчисления.
Наилучшие результаты в то время получили П. Ферма и И. Барроу. Выдающийся французский учёный Пьер Ферма (1601-1665) по сути умел находить производную произвольного многочлена от одной переменной. Пользуясь этим, он показал, как решать задачи на экстремум, в том числе - о вписывании в данный шар конуса наибольшего объёма, цилиндра наибольшей площади поверхности и т.п. Но само понятие производной он не выделил.

Исаак Барроу (1630-1677)
Применяя современные обозначения, доказанное им утверждение (теорема Барроу) можно записать так:
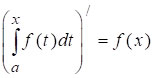
.
Таким образом была установлена взаимная обратимость операций дифференцирования и интегрирования. К доказательству этой зависимости И. Барроу подошёл двумя путями: кинематически и геометрически.
Теорема Барроу даёт возможность по результатам какого-либо дифференцирования или интегрирования найти результат обратной операции (т.е. установить первоначальную функцию). Используя этот результат, он решил ряд обратных задач на касательные.
С трудами И. Барроу ознакомились многие учёные, но они не поняли всеобщности и важности этой зависимости из-за громоздкой геометрической формулировки и пренебрежения аналитическими методами. Впоследствии учёные усовершенствовали формулировку и доказательство этой теоремы.
Это позволило теореме Барроу стать одной из важнейших в классическом математическом анализе. Именно она позволяет вычислять определённые интегралы (границы интегральных сумм) с помощью первоначальной функции.
Читайте также:

