Исследование алгебраических моделей реферат
Обновлено: 02.07.2024
ЗАДАЧИ:
обучающие:
- формирование ИКТ – грамотности:
- формирование способностей для идентификации информации (отбор уравнений, которые не решаются стандартными способами),
- формирование умений интегрировать информацию (анализ и сравнение различных методов решения уравнений, обобщение),
- формирование умений оценивать информацию (полезность и эффективность предложенных методов решения уравнений),
- формирование умений адаптировать информацию к конкретным условиям (построение и исследование математических моделей, применение их к конкретным уравнениям);
развивающие:
- формирование навыков деятельности, составляющих ИКТ-компетентность:
- управление – выделение нестандартных методов решения уравнений,
- интеграция – освоение предложенных методов,
- оценка – сравнение графического и числового методов,
- создание – умение применять данные методы при решении конкретных уравнений;
воспитательные:
- формирование познавательного интереса путем описания математических объектов автоматическими средствами представления данных;
- выработка у учащихся способности использовать компьютер при решении задач из различных предметных областей (математика);
- воспитание аккуратности, терпения, усидчивости.
ТИП УРОКА: изучение нового материала.
ФОРМА УРОКА: урок-исследование.
МЕТОДЫ ОБУЧЕНИЯ:
объяснительно-иллюстративный с применением презентации; частично поисковый, исследовательский; практический.ОБОРУДОВАНИЕ:
ПЛАН УРОКА:
ХОД УРОКА
3. Объяснение нового материала (Слайды 16-27).
Моделирование любых процессов начинается с записи формальной модели на языке определённой области знаний: математики, физики, химии, биологии, экономики.
На языке алгебры формальные модели записываются с помощью уравнений, точное решение которых основывается на поиске равносильных преобразований алгебраических выражений, позволяющих выразить переменную величину с помощью формулы.Определите виды уравнений и способы их решений.
Учащиеся определяют виды предложенных уравнений и способы их решений. Возможные ответы на поставленные вопросы приведены в таблице (Приложение7).Уравнение
1. 22х-18=6+10х
Известные члены – в правую часть, члены с неизвестными – в левую часть, привести подобные, найти неизвестный множитель.
2. x 2 + 6х – 27 = 0
х вынести за скобки и решить получившиеся линейные уравнения.
4. x 2 + 13х + 30 = 0
5. 9x 3 - х = 0
Разложить на множители и решить получившиеся линейные уравнения.
6. 3sin x - 2cos 2 x=0
По основному тождеству: cos 2 х = 1- sin 2 х, заменяем переменную sin х на t, решаем квадратное уравнение, затем получившиеся простейшие тригонометрические уравнения.
Левую и правую части представить в виде степени с основанием . Функция y= монотонна, можно приравнять показатели левой и правой частей уравнении, затем решить линейное уравнение.
8. log2 x 2 = 4
Использовать формулу логарифма степени и определение логарифма.
Ввести новую переменную , привести к квадратному уравнению и решить его.
Обсудим результаты, полученные в ходе решения.
Учащиеся записывают решение в тетрадях.Задача.
Дано: тригонометрическое уравнение x 3 - cos x = 0. Найти: корни уравнения.Формализованная модель.
a. Графическая (Слайды 29 – 32).
Необходимо построить графики функций: y= x 3 и y=cos x.
Затем, найти точки пересечения этих графиков, абсциссы которых и будут решениями уравнения.
Заполняем электронную таблицу значениями аргумента х от -2 до 2 с шагом 0,5 и формулами для определения значений функций y= x3 и y=cos x.Строим графики функций в одной системе координат.
5. Подведение итогов урока (Слайд 37).
Мы научились решать нестандартные уравнения с использованием:
![]()
В алгебре формальные модели записываются с помощью уравнений, точное решение которых основывается на поиске равносильных преобразований алгебраических выражений, позволяющих выразить переменную величину с помощью формулы. Точные решения существуют только для некоторых уравнений определённого вида, поэтому для большинства уравнений приходится использовать методы приближённого решения с заданной точностью. Такие уравнения проще и точнее можно решить путём построения интерактивных компьютерных моделей. На этом уроке исследуются методы решения уравнений, которые нельзя решить традиционно, путём построения компьютерных моделей.
![]()
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности
![]()
![]()
![]()
Конспект урока "Исследование алгебраических моделей"
· Исследование методов решения уравнений, которые нельзя решить традиционно, путём построения компьютерных моделей.
Моделирование любых процессов начинается с записи формальной модели на языке определённой области знаний: математики, физики, химии, биологии, экономики.
В алгебре формальные модели записываются с помощью уравнений, точное решение которых основывается на поиске равносильных преобразований алгебраических выражений, позволяющих выразить переменную величину с помощью формулы.
Точные решения существуют только для некоторых уравнений определённого вида (линейные, квадратные, тригонометрические и другие), поэтому для большинства уравнений приходится использовать методы приближенного решения с заданной точностью (графические или численные).
Например, нельзя точно найти корни уравнения x 2 = 8 – х путём равносильных алгебраических преобразований. Но такое уравнение можно решать приближённо графическими и численными методами.
![]()
Такие уравнения проще и точнее можно решить путём построения интерактивных компьютерных моделей.
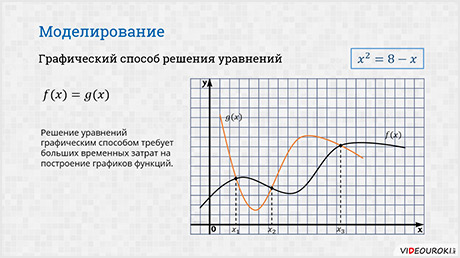
Итак, рассмотрим графический способ решения уравнений.
Нужно найти корни уравнения x 2 = 8 – х.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций. При использовании электронных таблиц, Microsoft Excel, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью, например, если использовать метод Подбор параметра.
![]()
Решим уравнение x 2 = 8 – х средствами Microsoft Excel.
Запускаем Microsoft Excel;
Для построения графика функции нам необходима таблица значений.
В ячейку В1 вводим число (-5), в ячейку С1 – число (-4,8);
выделим диапазон ячеек (В1;С1), подведём указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму чёрного крестика, протянуть маркер выделения вправо до значения 5.
В ячейку В2 вводим формулу: =В1^2 и скопируем содержимое ячейки Бэдва в диапазон ячеек (C2; AZ2). Вся строка выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
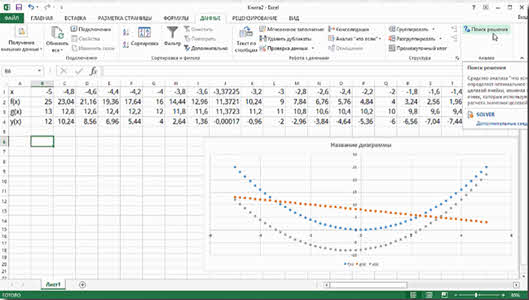
Мы построили таблицу значений, теперь построим графики функций. Для этого выделяем диапазон ячеек (A1; AZ2). Теперь на вкладке Вставка, в разделе диаграммы нажимаем на значок раскрывающегося списка Вставить точечную диаграмму. В раскрывшемся меню выбираем Точечная.
Итак, мы построили график функции f(x) = x 2 . Теперь на вкладка Работа с диаграммами выбираем вкладку Конструктор. В разделе Данные нажимаем Выбрать данные.
В окошке элементы легенды (ряды) нажимаем добавить. В раскрывшемся окне Изменение ряда выбираем Имя ряда – g(x), значения x – указываем диапазон ячеек (B1; AZ1). Значения y указываем диапазон ячеек (A3; AZ3).
![]()
Выделим первую точку пересечения и поднесём к ней указатель мыши, появится окошко комментария, в котором будет указана координата данной точки. Итак, первым корнем нашего уравнения будет (-3,4). Аналогично найдём второй корень. Второй корень нашего уравнения число 2,4.
Возможности электронных таблиц позволяют находить приближенные значения корней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения x точек пересечения графика функции y(x) с осью абсцисс.
Найдём приближённое решение уравнения с заданной точностью методом Подбор параметра.
Начнём с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен -3,4. В таблице значений функции этот аргумент размещается в ячейке J1.
В открывшемся диалоговом окне Подбор параметра в поле Значение ввести требуемое значение функции: 0. В поле Изменяя значение ячейки щёлкнем по ячейке J1.
В окне Результат подбора мы увидим информацию о величине подбираемого и подобранного значения функции:
В ячейке Джей один выводится подобранное значение аргумента (-3,37225) с требуемой точностью (0,0001).
Установить точность можно путём установки в ячейках таблицы точности представления чисел. Для этого нужно в меню Формат ячеек выбрать Число, а затем Числовой. Теперь установить требуемую точность.
Аналогично найдём приближенное значение второго корня уравнения с заданной точностью.
Итак, по графику определяем, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 2,4. В таблице значений функции этот аргумент размещается в ячейке AM1.
В открывшемся диалоговом окне Подбор параметра в поле Значение ввести требуемое значение функции: 0. В поле Изменяя значение ячейки щёлкнем по ячейке AM1.
В окне Результат подбора мы увидим информацию о величине подбираемого и подобранного значения функции:
В ячейке AM1 выводится подобранное значение аргумента (2,37229) с требуемой точностью (0,0001).
![]()
Рассмотрим ещё один способ решения уравнений средствами Excel
Часто при решении практических задач возникают ситуации, когда в Вашем распоряжении есть математическая модель исследуемого процесса, например, закон ценообразования, но Вы не знаете, при каком значении входящего в неё параметра можно достичь поставленной цели.
Решение таких задач можно искать методом перебора. Однако в лучшем случае на это уходит много времени.
В Excel такие способы решения реализованы как поиск значения аргумента, удовлетворяющего конкретному значению функции.
Найдём корни нашего уравнения x 2 = 8 – х с помощью средства анализа Поиск решения. А затем сравним полученные результаты.
Итак, нам необходимо вызвать программу Поиск решения и сообщить ей, где расположены данные. Для этого необходимо сначала загрузить её.
Откроим вкладку Файл и выберем пункт Параметры.
Далее выбираем команду Надстройки, а затем в окне Управление выбираем пункт Надстройки Excel. Нажимаем кнопку Перейти.
Теперь в окне Доступные надстройки установим флажок Поиск решения и нажимаем кнопку ОК.
После загрузки надстройки "Поиск решения" на вкладки Данные в группе Анализ становится доступна команда Поиск решения. Выбираем её, после чего перед нами открывается соответствующая форма.
Далее необходимо выполнить следующий алгоритм:
в ячейку A1 введём x, в ячейку B1 - значение, например, -5. В ячейку А2 введём y(x). В ячейку B2 необходимо ввести значение вспомогательной функции, то есть = x 2 -8 + х.
Теперь устанавливаем курсор в ячейку B2 и на вкладке Данные в группе Анализ нажимаем Поиск решения.
Введём координату ячейки с целевой функцией. В нашем случае это B2. (Заметим, что если перед этим установить курсор на ячейку B2, как мы и сделали, то ввод произойдёт автоматически).
Теперь хотелось бы получить второй корень. В задаваемом нами интервале видно, что график дважды пересекает ось Оx, следовательно, нужно найти ещё один корень. Однако, сколько бы мы не вызывали окно подбора параметра, компьютер с упорством, достойным лучшего применения, продолжает выдавать первый корень.
При поиске решения находится только оптимальное решение.
Также, обратите внимание, что во всех 3 вариантах решения, мы получили приблизительно равные корни нашего уравнения. Следовательно, можно сделать вывод, что уравнение мы решили правильно.
![]()
Теперь давайте попробуем решить другое уравнение на основе уже созданной модели.
Итак, решим уравнение х 2 -1=sinx.
Для построения графика функции нам необходима таблица значений. Она у нас уже есть, нам нужно только изменить значения в соответствующих ячейках. В ячейке B2 необходимо дописать (-1), и скопировать содержимое ячейки в диапазон (B2; AZ2). Теперь исправим значение в ячейке B3: запишем =sinB1, нажимаем Enter затем скопируем в диапазон (B3;AZ3).
Обратите внимание, графики функций автоматически изменились, и мы видим, что они пересекаются в двух точках. То есть, по графику мы на глаз можем определить, что приблизительно, корнями данного уравнения являются числа (-0,6) и (1,4).
![]()
Найдём более точные значения корней.
С помощью инструмента Поиск решения найдём более точное приближенное значение первого корня. Для этого в ячейку B7 запишем целевую функцию: = B6 ^2-1-sinB6. Ставим курсор в ячейку B6 и на вкладке Данные нажимаем Поиск решения. Заполним таблицу, итак, целевая функция у нас уже указана. Дальше ставим =0, затем указываем ячейку, в которую будет записано значение переменной. Нажимаем найти решение.
Получили значение одного корня. Он приблизительно равен (-0,63673).
Более точное приблизительное значение второго корня найдём методом Подбор параметра.
Итак, значения вспомогательной функции y(x) у нас уже посчитались. Находим по таблице значение, при котором знак вспомогательной функции меняется, это значение 1,4.
В открывшемся диалоговом окне Подбор параметра в поле Значение вводим требуемое значение функции: 0. В поле Изменяя значение ячейки щёлкнем по ячейке AG1.
Нажимаем Ок. В результате мы получили более точное приближенное значение второго корня: 1,4096.
Существует большое количество определений и концепций построения алгебр и логик.
В общем случае под алгеброй понимается математическая дисциплина, в которой рассматриваются операции над множествами. Совокупность операций обладает теми или иными свойствами, которые определяют ту или иную алгебру. Очевидно, что алгебра должна отражать те свойства, которыми обладают элементы, составляющие множества.
Под логикой в самом общем смысле понимается наука о законах мышления. В своем законченном виде логика как наука сформировалась в работах Аристотеля. Можно говорить и о логике Гегеля, Кантора и т. д. Все это разновидности, так называемой философской логики.
В разделах математики создан эквивалентный математический аппарат для описания различных философских логик в виде относительно большого числа математических или формальных логик. Естественно, что в любой алгебре используется операции математической логики, которая в свою очередь исследует логические преобразования над множествами, состоящими из символов. Однако существует и строгое определение логической алгебры как квазиупорядоченной алгебры, содержащей ряд идемпотентных операций, смысл которых будет уточнен далее. Направления математической логики и алгебры, имея много общих точек соприкосновения, развиваются самостоятельно.
Алгебраическое направление делится на два: алгебру и исчисление. Интерес к алгебраическим моделям существенно возрос в связи с развитием языков программирования, систем искусственного интеллекта, систем общения на естественном языке. С другой стороны, в классическом разделе кибернетики – теории автоматов также существенно усилилось влияние лингвистических методов. Автоматы стали трактоваться как некоторые лингвистические преобразователи (процессоры). В системах искусственного интеллекта (СИИ), которые представляют собой специального типа системы переработки информации, широко используется информационная алгебра.
Кроме того, следует иметь в виду то, что естественный язык и его математические (алгебраические) модели играют исключительную роль в СИИ как среда для моделирования процессов мышления и для обеспечения общения на естественном языке. И, конечно, ни одна модель СИИ не может обойтись без аппарата математической логики.
Логико-алгебраические модели
Алгебраические модели отличает от моделей с исчислением (в которых присутствуют связанные переменные) наличие свободных переменных. Осуществим попытку объединения всех моделей на основе лингвистической концепции.
Лингвистическая концепция интересна тем, что она принципиально обеспечивает рассмотрение с единых позиций не только логико-алгебраических моделей, но и моделей автоматно-лингвистических и моделей СИИ. Благодаря положенной в основу построения любой логико-алгебраической исходной предпосылки, состоящей в том, что, прежде всего, необходимо составить описание предметной области (для которой создается модель) на неформальном U-языке (конкретизировать его), все многообразие существующих модулей удается подчинить единой идеологии. Кроме того, благодаря этому утверждается концепция существования бесконечно большого числа моделей, каждая из которых ориентирована на конкретную предметную область (так же как профессиональный искусственный интеллект).
1. Классификация логико-алгебраических моделей.
Исторически многие логико-алгебраические модели в математике возникали независимо друг от друга, со своими автономными понятиями, терминологией и т. д. В пределах каждой модели исследователи старались создать законченную дедуктивную теоретическую конструкцию. В результате, было создано большое количество мало связанных между собой моделей.
Эти методы изложения интересны тем, что в них прослеживается индуктивный процесс формирования идеи. Многократно осуществлялись попытки объединения всех логико-алгебраических моделей на какой-то одной основе. В связи с этим широкое распространение получил теоретико-множественный подход к построению моделей, при котором любая модель рассматривается как некоторая совокупность операций над множествами. При этом одна модель отличается от другой элементами, из которых состоят множества, и набором операций с ними, которые отражают свойства этих элементов. Эта концепция позволяет рассмотреть с единых позиций все алгебры.
Однако при общей основе такой подход не обеспечивает функциональной, логической связи отдельных логико-алгебраических моделей. Поэтому появились другие направления дедуктивного объединения различных моделей, в частности структурное направление, характерной чертой которого является введение структурных компонентов во множества, входящие в логико-алгебраические модели.
Наибольший интерес представляет лингвистическое направление, в основном развитое в работах Х. Карри[1]. Появление большого числа логико-алгебраических моделей, разработанных в математике, вызвано потребностями практики, стремлением описать все встречающиеся ситуации, реальные системы. Поэтому в логиках и алгебрах появилось понятие предметной области, под которой понимается совокупность реальных объектов, отношений между ними и т. д. Каждая модель должна быть ориентирована на определенный класс конкретных предметных областей. Для решения проблемы семантики и прагматики модели, как правило, необходима процедура интерпретации ее на конкретную предметную область. В связи с этим появилась лингвистическая концепция, в основе которой лежит неформальный U-язык. С помощью этого языка производится описание предметной области. После чего в работу включаются более формализованные языки: А-язык (строго формализованный в семиотическом смысле) и О-язык (язык объектов). В этих языках вводится серия понятий и конструкций, с помощью которых можно построить логико-алгебраическую модель любой предметной (или как иногда говорят, проблемной) области. При этом достигается адекватность модели исходной предметной области и определенный автоматизм ее составления.
Исходный U-язык – неформальный язык, который близок к естественному языку, в частности, может сужаться до ограниченного естественного языка. Эта концепция построения логико-алгебраических моделей практически совпадает с общераспространенной концепцией построения систем искусственного интеллекта, в которой ограниченный естественный язык принимается как основа, некоторая среда для построения моделей профессионального искусственного интеллекта.
В лингвистическом направлении чрезвычайно плодотворным оказалось появление понятий свободных и связанных переменных. Это позволило отделить от алгебраических моделей модели типа исчислений: l-исчисление, исчисление предикатов, реляционное исчисление Кодда, в которых присутствуют связанные переменные.
В более широком смысле любое исчисление является некоторой математической моделью процесса перехода от посылок к следствию, проводимого по определенным правилам вывода. Именно так термин исчисление используется во многих разделах математики. При этом связанные переменные могут отсутствовать, но во многих математических моделях использование связанных переменных (через кванторы, l-операторы и т. д.) делает процесс перехода от посылок к следствию существенно более эффективным.
Алгебраические модели только со свободными переменными составляют вторую ветвь лингвистического направления, объединяющую булеву алгебру, реляционную алгебру, алгебру нечетких множеств. Особую ветвь составляют различные лингвистические системы, которые в алгебраическом смысле представляют собой так называемые полусистемы Туэ. Один из вариантов освобождения от связанных переменных, сохраняющий в то же время эффективность, которую они обеспечивают, представляет комбинаторная логика. Комбинаторная логика представляет в некотором смысле промежуточное звено между лингвистическом и структурным направлениями. В зависимости от структуры множеств и операций над ними структурные логико-алгебраические модели делятся на три совокупности моделей: слабой и средней алгебраизации (собственно модели) и сильной алгебраизации (алгебры). Среди моделей слабой алгебраизации имеет место алгебра графов. Содержание моделей средней алгебраизации представляют полусистемы Туэ, лингвистические системы с разными грамматиками и автономными моделями. Эта совокупность наиболее удачно поддается описанию структурными методами. Раздел моделей сильной алгебраизации составляют те же модели лингвистического направления со свободными переменными: булева алгебра, реляционная алгебра, алгебра нечетких множеств.
2. Основы лингвистического метода построения логико-алгебраических моделей.
Прежде всего, введем понятие языка исследования предметной области. Под предметной областью понимается конкретная область, для описания которой применяются алгебраические модели.
В соответствии с этим при описании предметной области должны фигурировать объекты, присущие данной предметной области. Опишем основные понятия языка исследования, а затем приведем способы построения объектов с помощью этого языка.
Введем в рассмотрение некоторые понятия. Теория – это некоторый аппарат, позволяющий выявлять истинные высказывания из набора всех высказываний. Система – частный случай теории. Для удобства работы с системами расплывчатый U-язык уточняется до А-языка, языка в так называемом семиотическом смысле, а последний еще более уточняется до языка объектов О-языка. В заключение рассмотрим понятие переменных, среди которых выделяются две группы: свободные и связанные, положенные в основу принятой классификации алгебраических моделей.
Результаты любого исследования предметной области одни люди сообщают другим посредством языка (назовем его U-языком). Невозможно исчерпывающе описать U-язык. Единственное, что утверждается – это то, что он содержит неопределенность, но всякое научное исследование связано с той же неопределенностью. Поэтому вместо исчерпывающего описания U-языка явно оговаривают лишь те случаи, которые могут быть неправильно истолкованы. U-язык обладает следующими особенностями:
1. для каждого конкретного контекста он единственен;
2. содержит формальную терминологию и другие лингвистические средства (например, использование букв для обозначения переменных, которые понимаются при определенной степени подготовленности);
3. он развивается (можно вводить новые термины и символику, либо использовать старые термины в новом смысле);
4. он неясен, однако, пользуясь им, можно достичь любой разумной степени точности.
Целый ряд проблем создания модели решается путем изучения языка, на котором они выражены. Такие исследования являются предметом изучения семиотики, науки о символах. Основное его понятие – язык.
Язык задается следующим образом:
1. фиксируется алфавит как набор символов (букв);
2. определяются правила, как из букв образовывать выражения (слова).
3. Основные понятия языка
При задании предметной области используются общеизвестные понятия, такие, как предложения, фразы, имена, высказывания, выражения и т. п.
Если изучать язык с точки зрения передаваемого им значения, то его выражения не образуют естественного класса символических комбинаций. Наибольший интерес представляет собой класс комбинаций, образующих объекты, к которым применяются правила построения предложений. Правила, определяющие предложения языка, называют его грамматикой, а комбинации символов, образующие грамматические единицы, – фразами языка.
Среди всех фраз выделяют имена, предложения и функторы. Имя называет некоторый объект. Предложение выражает утверждение. Функтор – это средство соединения фраз с целью образования других фраз. Фразы, соединяемые функтором, называют аргументами, а результат соединения – его значением.
![Нажмите, чтобы узнать подробности]()
Цель урока: Научиться создавать компьютерные модели для приближенного решения уравнений и систем уравнений.
ПРАКТИЧЕСКАЯ РАБОТА
Цель работы: Научиться создавать компьютерные модели для приближенного решения уравнений и систем уравнений.
Постановка задачи:
Корень или корни этого уравнения является точкой (или точками) пересечения графиков функций.
Графическое решение таких уравнений осуществим путем построения интерактивной компьютерной модели с помощью пакета электронных таблиц.
Порядок выполнения:
![]()
Будем строить таблицу (табулировать) две функции в отдельных столбцах таблицы.
I Столбец. Значение аргумента Х в интервале от [-5 до 5].
Чем меньше выберем шаг табуляции, тем точнее получится результат. На нашей модели выберем шаг табуляции равный 0,5.
II Столбец. Рассчитаем значение функции f1(X) = SIN(X).
III Столбец. Рассчитаем значение функции f2(X) = 3X -2.В точках, где значение функций будут примерно одинаковыми и будет решением уравнения.
Для выбранной функции это будет примерно в т.Х~1.
f1(1) = SIN(1)~0,84; f2(1) = 3*1 -2~1.С помощью графиков функции подтверждаем расчеты. Вид таблицы и полученные графики представлены на отдельном листе( приложение )
Для получения более точного расчета можно протабулировать те же функции в более близких к решению интервале. Например:[-1,2] с шагом 0,1. В этом случае получим более точное решение Х~0,9.
Результат показать преподавателю.
Задание 1. Рассчитать с помощью графиков корни уравнения
Y(X) =1/2*X 2 – 3*X + 2
для значений аргумента в интервале [-5, 8] c шагом 0,5. Найти X при которых Y(X)=0
Задание 2. Рассчитать с помощью графиков корни уравнения
для значений аргумента в интервале [-1,4;1,4] c шагом 0,5. Найти X при которых Y(X)=0
Задание 3. Рассчитать с помощью графиков корни уравнения
Y(X) =1/2*X 2 – 3*X + 2
для значений аргумента в интервале [-5, 8] c шагом 0,5. Найти X при которых Y(X)=0
Задание 4. Рассчитать с помощью графиков корни уравнения
Y(X) =sin 2 (x) - cos 2 (x)
для значений аргумента в интервале [-3,14, 3,14] c шагом 0,2. Найти X при которых Y(X)=0
Задание 5. Рассчитать с помощью графиков корни уравнения
Y(X) =(Х-1) 2 -9 - (4-Х) 2
для значений аргумента в интервале [-5, 5] c шагом 0,5. Найти X при которых Y(X)=0
Задание 6. Рассчитать с помощью графиков корни уравнения
для значений аргумента в интервале [1, 2] c шагом 0,1. Найти X при которых Y(X)=0
Задание 7. Рассчитать с помощью графиков корни уравнения Y(X) =0,1X 2 – Xcos(X)
для значений аргумента в интервале [1;2] c шагом 0,1. Найти X при которых Y(X)=0
Читайте также: