Характеристическое свойство фигуры реферат
Обновлено: 04.07.2024
Многоугольники
Плоские замкнутые ломаные;
Плоские замкнутые ломаные без самопересечений;
Части плоскости, ограниченные ломаными.
Связанные определения
Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
Углом (или внутренним углом) многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, и находящийся во внутренней области многоугольника. В частности, угол может превосходить 180°, если многоугольник невыпуклый.
Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол это разность между 180° и внутренним углом
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с чётырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
Многоугольник с n вершинами называется n-угольником.
Плоским многоугольником называется фигура, которая состоит из многоугольника и ограниченной им конечной части площади.
он лежит по одну сторону от любой прямой, соединяющей его соседние вершины. (то есть продолжения сторон многоугольника не пересекают других его сторон);
он является пересечением (то есть общей частью) нескольких полуплоскостей;
любой отрезок с концами в точках, принадлежащих многоугольнику, целиком ему принадлежит.
Выпуклый многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности.
Выпуклый многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.
Свойства
Сумма внутренних углов плоского выпуклого n-угольника равна (в градусах) и (в радианах).
Число диагоналей всякого многоугольника равно n(n − 3) / 2, где n — число сторон
Четырёхугольник — это многоугольник, содержащий четыре вершины и четыре стороны. Различают выпуклые и невыпуклые четырёхугольники
Виды четырёхугольников
Параллелограмм — четырёхугольник, у которого все противоположные стороны параллельны;
Прямоугольник — четырёхугольник, у которого все углы прямые;
Ромб — четырёхугольник, у которого все стороны равны;
Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.
вогнутый выпуклый скрещенный






равнобедренная трапеция параллелограмм выпуклый ромбоид
равнобокая симметричные стороны диагонали перпендикулярны


прямые углы равнобедренный
Свойства
Сумма углов четырёхугольника равна .
Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
Шесть расстояний между четырьмя произвольными точками плоскости, взятыми попарно, связаны соотношением:

.
Свойство диагоналей выпуклого четырёхугольника
Рисунок 1 рисунок 2
рисунок 4 рисунок 3
рисунок 6 рисунок 7
На рисунке 1 диагонали AC и BD выпуклого четырехугольника ABCD пересекаются в точке O, а диагонали EG и FH невыпуклого четырехугольника EFGH не пересекаются. Это свойство диагоналей характерно для любого выпуклого (и соответственно невыпуклого) четырехугольника. Однако при всей его очевидности строгое обоснование этого свойства оказывается достаточно сложным. Предварительно рассмотрим два вспомогательных утверждения. Напомним, что согласно одной из аксиом планиметрии каждая прямая а разделяет плоскость на две полуплоскости так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а. Прямая а называется границей каждой из этих полуплоскостей, ее точки не принадлежат ни одной из полуплоскостей.
Утверждение 1. Если начало луча AB (точка A) лежит на прямой а,а точка B-в какой-то полуплоскости с границей а, то и весь луч лежит в этой полуплоскости (рисунок 3)
Второе утверждение связано с понятием внутренней области неразвернутого угла. Это понятие было в 7-м классе на основе наглядных представлений. Дадим точное определение.
Рассмотрим неразвернутый угол ACB (рисунок 4). Прямая BC разделяет всю плоскость на две полуплоскости. В одной из них лежит луч CA. Обозначим эту полуплоскость буквой a. Точно так же прямая AC разделяет всю плоскость на две полуплоскости, в одной из которых лежит луч CB. Обозначим эту полуплоскость буквой p. Общая часть полуплоскостей а и p называется внутренней областью угла ACB.
Утверждение 2. Если точки А и В лежат на разных сторонах неразвернутого угла с вершиной С, а точка D лежит внутри угла АСВ (т.е. в его внутренней области), то луч СD пересекает отрезок АВ (рисунок 5)
С наглядной точки зрения утверждения 1 и 2 совершенно очевидны. Строгое обоснование можно провести на основе аксиом планиметрии. Вернемся теперь к свойствам диагоналей выпуклого и невыпуклого четырехугольников.
Теоремы. Диагонали выпуклого четырехугольника пересекаются, а невыпуклого не пересекаются.
Рассмотрим выпуклый четырехугольник ABCD (рисунок 6). Докажем сначала, что вершина С лежит внутри угла BAD. Прямая AD разделяет плоскость на две полуплоскости. Так как четырехугольник выпуклый, то его вершины В и С лежат в одной из этих полуплоскостей и, значит, вершина С лежит в той же полуплоскости, что и луч АВ. Обозначим эту полуплоскость буквой а. Аналогично прямая АВ разделяет плоскость на две полуплоскости, причем вершина С и луч AD лежат в одной из этих полуплоскостей. Обозначим ее p. Таким образом,точка С лежит как в полуплоскости а, так и в полуплоскости р. Но общая часть этих полуплоскостей и есть внутренняя область угла BAD, поэтому точка С лежит внутри угла BAD.
Точно так же можно доказать, что луч DB пересекает отрезок АС. Ясно, что точкой их пересечения является та же самая точка О.
Рассмотрим теперь невыпуклый четырехугольник ABCD.
Пусть вершины С и D лежат по разные стороны от прямой АВ (рисунок 7). Тогда в силу утверждения 1 лучи АС и ВD лежат в разных полуплоскостях с границей АВ и, следовательно, не имеют общих точек. Значит, и отрезки АС и ВD не имеют общих точек, т.е. диагонали АС и ВD четырехугольника АВСD не пересекаются. Теорема доказана.
Следствие. Если диагонали четырехугольника пересекаются, то этот четырехугольник выпуклый.
Характеристическое свойство фигуры
Итак, нами было доказано , что диагонали выпклого четырехугольника пересекаются, и обратно, если диагонали четырехугольника пересекаются, то этот четырехугольник выпуклый. Таким образом, выпуклые четырехугольники обладают определенным свойством, которое выделяет их среди всех четырехугольников, отличает от других (невыпуклых) четырехугольников. Такое свойство геометрических фигур называется характеристическим свойством.
Характеристическое свойство может быть положено в основу определения геометрической фигуры. Например, можно дать такое определение выпуклого четырехугольника: четырехугольник называется выпуклым, если его диагонали пересекаются.
Это определение равносильно “старому” выпуклого четырехугольника, (напомним, что “старое” определение относилось к любым многоугольникам, в том числе и к четырехугольникам). В самом деле, если четырехугольник является выпуклым по “старому” определению, то по доказанной ранее теореме его диагонали пересекаются и, значит, он является выпуклым по “новому” определению, т.е. его диагонали пересекаются, то согласно следствию из той же теоремы он является выпуклым и по “старому” определению.
Утверждение о характеристическом свойстве фигуры можно сформулировать с использованием словосочетания “тогда и только тогда”. Например: диагонали четырехугольника пересекаются тогда и только тогда, когда он является выпуклым.
В этом предложении содержаться два утверждения. Первое (оно связано со словом “тогда”) выражает свойство выпуклого четырехугольника: если четырехугольник выпуклый, то его диагонали пересекаются. Второе (обратное) утверждение связано со словом “только тогда”, оно выражает признак выпуклого четырехугольника: если диагонали четырехугольника пересекаются, то четырехугольник выпуклый.
Площадь
, где d1, d2 — диагонали и α — угол между диагоналями.
, где e, f — длины диагоналей, a, b, c, d - длины сторон.
, где p — полупериметр. Из этой формулы для вписанных 4-угольников следует формула Брахмагупты.
Особые случаи

Если 4-угольник и вписан и описан, то .
История
В древности египтяне и некоторые другие народы использовали в качестве площади четырёхугольника неверную формулу — произведение полусумм его противоположных сторон a, b, c, d [1] :

.

Цель – показать необходимость изучения этой науки (геометрии), которая дает возможность понять, а также рассмотреть значение геометрических законов и закономерностей, их практическое применение при проектировании и постройке сооружений.
Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.
Основными геометрическими фигурами на плоскости являются точка и прямая. Этим фигурам в геометрии не даётся определений. Неопределяемыми геометрическими фигурами на плоскости являются точка и прямая. Точки принято обозначать прописными латинскими буквами: А, В, С, D …. Прямые обозначаются строчными латинскими буквами: а, b, с, d ….
1.Основные геометрические понятия.
Основные геометрические понятия возникли еще в доисторические времена. Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий. Одним из первых достижений абстрактного мышления древнего человека стало понимание прямой линии.
Прямая не проходит через точку, если точка не принадлежит ей.
Пряма́я — одно из фундаментальных понятий геометрии.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой).Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками. Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.
К основным свойствам прямой относятся:
Черед две различные точки проходит одна единственная прямая. Следовательно две прямые не могут иметь более одной общей точки.
Две разные прямые, имеющие общую точку, пересекаются в ней. В связи с тем, что две точки определяют прямую, проходящую через них, прямую обозначают сочетанием букв, к примеру, прямая АВ, прямая PQ.
Точка М, лежащая на прямой а, разбивает её на две части. Каждая из которых называется полупрямой или лучом. Точка М служит началом каждого их этих лучей. Две точки М и N разбивают прямую на три части: два луча МР и NQ и отрезок MN.
Прямая разбивает плоскость на 2 части. Часть плоскости лежащая по одну сторону от этой прямой, называется полуплоскостью.
Если прямые не имеют общих точек, говорят, что они параллельны.
Если две прямые имеют одну общую точку, говорят, что они пересекаются в этой точке.
Две прямые в трёхмерном евклидовом пространстве скрещиваются, если не существует плоскости, их содержащей. Иначе говоря, две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными.
2. Параллелограмм.
Параллелограмм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — черта, линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Признаки параллелограмма:
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий:
1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник - параллелограмм
2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм
3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник - параллелограмм
Параллелограмм, у которого все углы прямые, называется прямоугольником.
Теорема. Если в параллелограмме диагонали равны, то он является прямоугольником.
Параллелограмм, у которого все стороны равны, называется ромбом.
Теорема. Если в параллелограмме диагонали перпендикулярны, то он является ромбом.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Расстояние между основаниями называется высотой трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Отрезок, соединяющий середины диагоналей, равен полуразности оснований.
В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной.
Свойства равнобедренной трапеции.
Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
В равнобедренной трапеции углы при любом основании равны.
В равнобедренной трапеции длины диагоналей равны.
Если трапецию можно вписать в окружность, то она равнобедренная.
Около равнобедренной трапеции можно описать окружность.
Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
4.Окружность.
Окружность – это плоская замкнутая линия, все точки которой находятся на одинаковом расстоянии от некоторой точки (точки О), которая называется центром окружности.
(Окружность — геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.)
Круг – это часть плоскости, ограниченная окружностью. Точка О также называется центром круга. Расстояние от точки окружности до её центра, а также отрезок, соединяющий центр окружности с её точкой, называется радиусом окружности/круга.
Хорда - греческое - струна, стягивающая что-то
Диаметр - "измерение через"
Углы могут встречаться во все более возрастающем количестве, приобретать, соответственно, все больший разворот – пока не исчезнут окончательно и плоскость не станет кругом. Это очень простой и одновременно очень сложный случай, о котором мне хотелось бы поговорить подробно. Здесь необходимо отметить, что как простота, так и сложность обусловлены отсутствием углов. Круг прост, поскольку давление его границ, в сравнении с прямоугольными формами, нивелировано – различия здесь не так велики. Он сложен, поскольку верх неощутимо перетекает в левое и правое, а левое и правое – в низ.
В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении. В школе изучается много полезных свойств окружности. Одной из самых красивых теорем является следующая: проведем через заданную точку прямую, пересекающую заданную окружность, тогда произведение расстояний от этой точки до точек пересечения окружности с прямой не зависит от того, как именно была проведена прямая. Этой теореме около двух тысяч лет. Эта фигура получается, если провести дуги окружностей с центрами в вершинах равностороннего треугольника, соединяющие две другие вершины. Если провести к этой фигуре две параллельные касательные, то расстояние между ними будет равно длине стороны исходного равностороннего треугольника, так что такие катки ничем не хуже круглых. В дальнейшем были придуманы и другие фигуры, способные выполнять роль катков.
У каждого треугольника имеется, и притом единственная, окружность девяти точек. Это окружность, проходящая через следующие три тройки точек, положение которых определено для треугольника : основания его высот D1 D2 и D3, основания его медиан D4, D5 и D6 середины D7, D8 и D9 отрезков прямых от точки пересечения его высот Н до его вершин. Эта окружность, найденная в XVIII в. великим ученым Л. Эйлером (поэтому ее часто также называют окружностью Эйлера), была заново открыта в следующем столетии учителем провинциальной гимназии в Германии. Звали этого учителя Карл Фейербах (он был родным братом известного философа Людвига Фейербаха). Дополнительно К. Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это -точки ее касания с четырьмя окружностями специального вида. Одна из этих окружностей вписанная, остальные три - вневписанные. Они вписаны в углы треугольника и касаются внешним образом его сторон. Точки касания этих окружностей с окружностью девяти точек D10, D11, D12 и D13 называются точками Фейербаха. Таким образом, окружность девяти точек является в действительности окружностью тринадцати точек. Окружность эту очень легко построить, если знать два ее свойства. Во-первых, центр окружности девяти точек лежит в середине отрезка, соединяющего центр описанной около треугольника окружности с точкой Н- его ортоцентром (точка пересечения его высот). Во-вторых, ее радиус для данного треугольника равен половине радиуса описанной около него окружности.
5.Треугольник.
Треуго́льник (в евклидовом пространстве) — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника.
Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла.
Вершины — три точки А, В и С. Стороны — отрезки АВ, ВС и СА.
Углы — ∟ ВАС, ∟ СВА и ∟ АСВ.
Периметр треугольника — сумма длин трех сторон треугольника.
Медиана треугольника (m)— отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Биссектриса треугольника (b) — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. Высота треугольника (h)— перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке.
Теорема. Сумма углов треугольника 180°. Каждая сторона треугольника меньше суммы двух других сторон.
1) против большей стороны лежит больший угол.
2) против большего угла лежит большая сторона.
В прямоугольном треугольнике гипотенуза больше катета
Классификация треугольников по углам. В треугольнике может быть только один тупой угол. В треугольнике может быть только один прямой угол. По сторонам.
Треугольник называется равнобедренным, если две его стороны равны.
Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
5.1. Теоремы треугольника.
В равнобедренном треугольнике углы при основании равны.
Теорема
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Равносторонний треугольник — все стороны и углы равны.
Если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
В равных треугольниках против соответственно равных сторон лежат равные углы.
5.2.Признаки треугольника.
ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
5.3.Прямоугольный треугольник.
СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
• Сумма двух острых углов прямоугольного треугольника равна 90°.
• Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
• Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету.
5.4. История изучения треугольника.
6.Многоугольник.
Многоугольник — фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.
Точки А, В, С, D, Е… — вершины многоугольника. Отрезки АВ, ВС, CD, DE, ЕА,… - стороны многоугольника.
Периметр многоугольника (гречечкое пери - вокруг, около) — сумма длин всех сторон.
Многоугольник с n вершинами называется n-угольником; он имеет n сторон.
Две вершины многоугольника, принадлежащие одной стороне, называются соседними.
Диагональ многоугольника (греческое dia - через, gonia - угол, т.е. проходящая через углы) — отрезок, соединяющий любые две несоседние вершины.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая — внешней областью многоугольника. Фигуру, состоящую из сторон многоугольника и его внутренней области, также называют многоугольником.
Многоугольник называется выпуклым:
1) если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины
2) если вместе с любыми своими 2 точками он содержит и соединяющий их отрезок.
Сумма углов выпуклого п-угольника равна (n- 2) 180°.
Многоугольником может называться замкнутая ломаная с самопресечениями и правильные звёздчатые многоугольники.
Площадь многоугольника — это величина той части плоскости, которую занимает многоугольник.
1) равные многоугольники имеют равные площади;
2) если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
3) площадь квадрата равна квадрату его стороны.
7. Многранники. Виды многранников
В современном мире нас окружает множество построек состоящих из сложных геометрических фигур, большинство из которых являются многогранниками. Примеров тому очень много, достаточно посмотреть по сторонам и мы заметим что здания, в которых мы живём, магазины, в которые ходим, школы и детские сады и т.д. представлены в виде многогранников.
Призма – это многогранник, две грани которой ABCDE и abcde ( основания призмы ) – равные многоугольники с соответственно параллельными сторонами, а остальные грани ( AabB, BbcC и т.д. ) - параллелограммы, плоскости которых параллельны прямой ( Aa, или Bb, или Cc и т.д. По основанию:
-Небоскрёб Flat Iron (Утюг) на пересечении Бродвея и Пятого Авеню. Построен в 1902 году. 21 этаж, 87 метров
-Пентагон — здание Министерства обороны США в форме пятиугольника. Находится в штате Вирджиния недалеко от Вашингтона.
-Наклонная призма – боковое ребро наклонено к основанию под углом отличны от 90є.
Прямая призма – боковое ребро расположено перпендикулярно к основанию.
7.2. Параллелепипед
Параллелепипед - призма, в основании которой находится параллелограмм.
Наклонный, Прямой, Прямоугольный – это прямой параллелепипед,
в основании которого прямоугольник.
Куб – это прямой параллелепипед,
все грани которого квадраты
7.3. Пирамида
Пирамида – это многогранник, одна из граней которого – произвольный n-угольник, а остальные “n” граней – треугольники, имеющие общую вершину.
-Университетский волейбольно-баскетбольный стадион в Калифорнии
В основании - Квадрат
-Торговый центр в Турции
Цилиндр – это тело, ограниченное частью замкнутой цилиндрической поверхности и частью двух плоскостей, параллельных между собой
Водонапорная башня в Минске, Нефтехранилища, Небоскреб в США
Конус - это геометрическое тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины и частью пересекающей её плоскости.
Как самостоятельные сооружения конусы в строительстве не используются. Практически всегда они составляют какую-то часть здания, например крыши и архитектурные украшающие детали.
Также в строительстве используют конические сваи.
7.6. Сфера и шар.
Сфера – это множество всех точек пространства, находящихся на положительном расстоянии R от данной точки О, называемой центром сферы.
Шар – это множество всех точек пространства, расстояние которых от данной точки не превосходит заданного положительного числа R. Шар получается при вращении полукруга относительно диаметра.
Шаровой слой – это часть шара, заключенная между двумя параллельными плоскостями.
Шаровой сегмент – это часть шара, отсекаемая от него плоскостью.
ТРК Вояж, г. Санкт-Петербург, Здание в Париже (Франция)
Здание Национального Конгресса в США
Итак, при постройке, как современных зданий, так и зданий прошлых веков необходимы знания геометрии. Архитектурное формообразование с помощью геометрических построений сохраняется во всех случаях. Эта проблема стояла перед архитекторами прошлых веков, не исчезла она и сегодня.
7.7. Двойной квадрат
Два квадрата, сложенные вместе, образуют двойной квадрат. Сложив два двойных квадрата, получим квадрат, повторяющий своими очертаниями исходный квадрат. Это простое аддитивное свойство квадрата широко использовалось в архитектуре эпохи Возрождения.
7.8. Восьмиугольные звезды.
Использование восьмиугольных звезд в архитектурных конструкциях не вызывает никаких сомнений. Автором этого проекта является Леонардо да Винчи.
Золото́е сече́ние (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

Помогите другим пользователям — будьте первым, кто поделится своим мнением об этой презентации.
Аннотация к презентации
Смотреть презентацию онлайн с анимацией на тему "Характеристическое свойство фигуры." по математике. Презентация состоит из 11 слайдов. Для учеников 9 класса. Материал добавлен в 2021 году.. Возможность скчачать презентацию powerpoint бесплатно и без регистрации. Размер файла 1.57 Мб.
Содержание

Характеристическое свойство фигуры.

Слайд 2
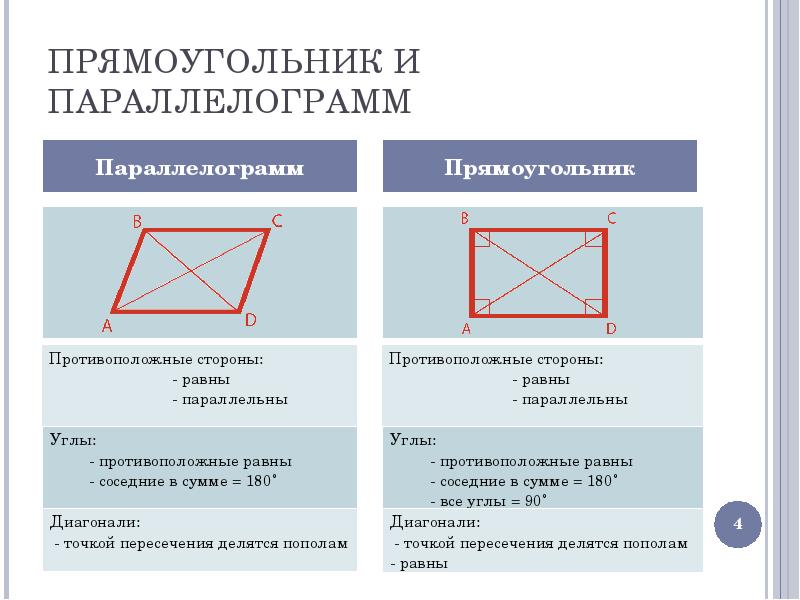
Характеристические свойства прямоугольника.
Параллелограмм, у которого все углы прямые, называется прямоугольником.

Слайд 3
Свойства прямоугольника Противоположные стороны прямоугольника равны. Все углы прямоугольника равны. Диагонали прямоугольника равны. Диагонали прямоугольника пересекаются и точкой пересечения делятся пополам. Диагонали прямоугольника делят его на два равных треугольника. В прямоугольника сумма углов, прилегающих к одной стороне, равна 180 °.

Слайд 4
Признаки прямоугольника Если в параллелограмме все углы равны, то этот параллелограмм является прямоугольником. Если в параллелограмме один угол прямой, то этот параллелограмм является прямоугольником. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником. Если в четырехугольнике три угла прямые, то этот четырехугольник является прямоугольником. Если в четырехугольнике все углы равны, то этот четырехугольник является прямоугольником.

Слайд 5
Это интересно. Если в прямоугольнике с неровными смежными сторонами провести биссектрисы его углов, то при их пересечении образуется прямоугольник.

Слайд 6
Ромб - параллелограмм, у которого все стороны равны. Диагонали ромба взаимно перпендикулярны, и делят его углы пополам. Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны, АВ || CD, AD || ВС.

Слайд 7
Признаки ромба: Параллелограмм является ромбом, если: Две его смежные стороны равны. Его диагонали перпендикулярны. Одна из диагоналей является биссектрисойего угла.

Слайд 8
Это прямоугольник,у которого все стороны равны. Признаки квадрата: Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.

Слайд 9
Свойства квадрата Все углы квадрата прямые; Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Слайд 10
Окру́жность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Свойства окружности Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая). Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну. Точка касания двух окружностей лежит на линии, соединяющей их центры.

Слайд 11
Вписанные углы, опирающиеся на одну и ту же дугу, равны Касательные к окружности, проведенные из одной точки, равны.
Вы можете изучить и скачать доклад-презентацию на тему Прямоугольник. Ромб. Квадрат. Презентация на заданную тему содержит 13 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!











ЦЕЛИ УРОКА: Повторить понятие параллелограмма; Дать определение прямоугольника, ромба, квадрата. Познакомиться со свойствами данных фигур; Научиться применять свойства при решении задач.
ПРИЗНАК ПРЯМОУГОЛЬНИКА Вопрос: любой четырехугольник, в котором диагонали равны, является прямоугольником? Ответ: не всегда
СВОЙСТВА РОМБА 1. Противоположные стороны попарно параллельны: AB//CD, AD//BC 2. Все стороны равны: AD=DC=CB=AB 3. Противоположные углы равны: ∟A=∟C, ∟D=∟B 4. Соседние углы в сумме дают 180˚: ∟A+∟B=180˚, ∟C+∟D=180˚ 4. Диагонали ромба пересекаются под прямым углом: AC ┴ BD 5. Диагонали ромба точкой пересечения делятся пополам: AО=CО, ОB =DО
СВОЙСТВА КВАДРАТА 1. Все стороны равны 2. Все углы прямые 3. Диагонали равны 4. Диагонали точкой пересечения делятся пополам 5. Диагонали пересекаются под прямым углом
ПРИЗНАКИ КВАДРАТА Если в прямоугольнике диагонали перпендикулярны – это квадрат Если в ромбе диагонали равны – это квадрат Если в параллелограмме диагонали перпендикулярны и равны – это квадрат
Равенства. Неравенства. Знаки" width="120" src="https://myslide.ru/documents_2/9470990cdd1ac60ec110d2e3b281836e/thumb.jpg" original="/documents_2/9470990cdd1ac60ec110d2e3b281836e/thumb.jpg">
99366 99346 99373 99367 99347 99363 99344 99349 99372 99352 99355 99357 99345 99362 99364 99353 99369 99358 99368 99350 99359 99361 99354 99348 99371 99360 99351 99370 99365 99356
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Мы в социальных сетях
Читайте также:

