Единственность и существование решения первой начально граничной задачи для уравнения струны реферат
Обновлено: 02.07.2024
Функциональные, дифференциальные и интегральные уравнения, Сабитов К.Б., 2005.
Функции многих переменных.
1. Пространство Rn. До сих пор мы изучали функции одной независимой переменной. На практике часто возникают случаи, когда какая-нибудь величина зависит от двух или большего числа независимых переменных. Например, площадь S прямоугольника является функцией двух независимо друг от друга изменяющихся переменных - длин сторон прямоугольника а и b. Эта функция задается равенством : S = a b.
Объем V прямоугольного параллелепипеда есть функция трех независимо друг от друга изменяющихся величин - длин ребер параллелепипеда a,b,c: V = abс.
Работа А постоянного электрического тока на участке цепи зависит от разности потенциалов U на концах участка, силы тока I и времени t. Эта функциональная зависимость задается формулой: А = IUt.
Прежде чем перейти к изучению функций многих переменных рассмотрим множества, на которых эти функции задаются.
Оглавление
Предисловие
Глава 1. Вспомогательные сведения из курса математического анализа
§1. Действительные числа
1. Рациональные числа
2. Иррациональные числа
3. Ограниченные подмножества множества действительных чисел
4. Приближение действительных чисел рациональными
§2. Числовые функции
§3. Последовательности. Предел последовательности
§4. Предел функции
§5. Непрерывность функции
§6. Обратная функция. Существование и непрерывность обратной
функции
§7. Производная, дифференцируемость, дифференциал функции
§8. Неопределенный интеграл
§9. Определенный интеграл
§10. Несобственные интегралы
1. Несобственные интегралы первого рода
2. Несобственные интегралы второго рода
3. Главное значение несобственного интеграла
§11. Ряды
1. Числовые ряды
2. Функциональные последовательности и ряды
3. Степенные ряды
4. Тригонометрические ряды
5. Ортогональные системы функций
§12. Кривые в пространстве. Длина кривой
§13. Функции многих переменных
1. Пространство Rn
2. Последовательности точек Rn
3. Функции многих переменных
§14. Предел и непрерывность функций многих переменных
1. Предел функций многих переменных
2. Непрерывность функций многих переменных
§15. Частная производная, дифференцируемость и дифференциал
функций многих переменных
1. Частная производная
2. Дифференцируемость функции
3. Производная по направлению. Градиент
4. Частные производные высших порядков
5. Дифференциалы высших порядков
6. Замена переменных
§16. Локальный экстремум функции многих переменных
§17. Неявные функции. Зависимость функций
1. Неявные функции
2. Зависимость функций
§18. Двойные интегралы
1. Понятие квадрируемости плоской фигуры и ее площади (меры)
2. Двойной интеграл
3. Условия существования двойного интеграла
4. Свойства двойного интеграла
5. Вычисление двойного интеграла
6. Замена переменных в двойном интеграле
§19. Тройные и n - кратные интегралы
1. Понятие кубируемости тела и его объема
2. Тройной интеграл
3. n - кратные интегралы
4. Несобственные кратные интегралы
§20. Криволинейные интегралы
1. Криволинейные интегралы первого рода
2. Криволинейные интегралы второго рода
3. Формула Грина. Условия потенциальности векторного поля
§21. Поверхностные интегралы
1. Поверхности. Площадь поверхности. Ориентация поверхности
2. Поверхностный интеграл первого рода
3. Поверхностные интегралы второго рода
4. Интегральные теоремы Остроградского - Гаусса и Стокса. Условия потенциальности векторного поля в пространстве
§22. Интегралы, зависящие от параметра. Эйлеровы интегралы
1. Равномерное стремление функции к предельной функции
2. Свойства собственных интегралов, зависящих от параметра
3. Несобственные интегралы первого рода, зависящие от параметра
4. Несобственные интегралы второго рода, зависящие от параметра
5. Кратные интегралы, зависящие от параметра
6. Примеры вычисления несобственных интегралов
7. Эйлеровы интегралы
§23. Комплексные числа и функции
1. Комплексные числа
2. Последовательности и ряды комплексных чисел
3. Комплексные функции комплексной переменной
4. Аналитические и гармонические функции
5. Элементарные функции. Формулы Эйлера
6. Теорема единственности аналитической функции. Аналитическое продолжение.
Глава 2. Функциональные уравнения
§1. Функциональное уравнение, определяющее показательную
функцию
§2. Функциональное уравнение, определяющее логарифмическую
функцию
§3. Функциональное уравнение, определяющее степенную функцию
§4. Функциональное уравнение, определяющее линейную функцию
§5. Функциональные уравнения, определяющие тригонометрические
функции синус и косинус
§6. Задачи на решение функциональных уравнений
Задачи для самостоятельной работы
Глава 3. Дифференциальные уравнения
§1. Основные понятия дифференциальных уравнений
§2. Простейшие дифференциальные уравнения первого порядка, разрешимые в явном виде
1. Дифференциальные уравнения вида у = f(x)
2. Дифференциальные уравнения с разделенными переменными
3. Дифференциальные уравнения с разделяющимися переменными
4. Однородные дифференциальные уравнения
5. Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли и Риккати
6. Дифференциальное уравнение в полных дифференциалах. Интегрирующий множитель
§3. Теоремы существования и единственности решения задачи Коши для дифференциальных уравнений
1. Теорема существования и единственности решения задачи Коши для дифференциальных уравнений первого порядка
2. Теорема существования и единственности решения задачи Коши для нормальной системы дифференциальных уравнений
3. Теорема существования и единственности решения задачи Коши для дифференциального уравнения n - го порядка
§4. Уравнения первого порядка, не разрешенные относительно производной. Особые решения
1. Задача Коши
2. Уравнения Лагранжа и Клеро
3. Особые решения
§5. Зависимость решения от начальных условий, правой части и параметров
§6. Линейные однородные дифференциальные уравнения второго порядка
§7. Линейные неоднородные дифференциальные уравнения второго порядка. Метод вариации постоянных
§8. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод неопределенных коэффициентов
§9. Решение линейных дифференциальных уравнений с переменными коэффициентами с помощью степенных рядов. Уравнение Бесселя. Гипергеометрическое уравнение
1. Теорема существования и единственности решения
2. Уравнение Бесселя. Функции Бесселя
3. Модифицированные функции Бесселя
4. гипергеометрическое уравнение. Функции Гаусса
§10. Качественные свойства решений линейных уравнений второго порядка
§11 Краевые задачи для линейных дифференциальных уравнений второго порядка
1. Основные определения и понятия. Формула Грина
2. Единственность и существование решения краевой задачи. Функция Грина
3. Примеры
§12. Система линейных дифференциальных уравнений первого порядка
1. Однородная система линейных дифференциальных уравнений
2. Линейная неоднородная система дифференциальных уравнений. Метод вариации произвольных постоянных
3. Линейная однородная система с постоянными коэффициентами
§13. Устойчивость решений дифференциальных уравнений
§14. Особые точки дифференциальных уравнений первого порядка
§15. Автономные системы дифференциальных уравнений и их
фазовые пространства
1. Механическая интерпретация нормальной системы дифференциальных уравнений первого порядка
2. Свойства решений автономных систем
3. Предельное поведение траекторий. Предельные циклы
4. Функция последования
5. Ламповый генератор
§16. Задачи на применение дифференциальных уравнений первого порядка
§17. Применение линейных дифференциальных уравнений второго
порядка к изучению колебательных процессов
1. Математические модели колебательных систем
2. Свободные колебания
3. Вынужденные колебания. Явление резонанса
Задачи для самостоятельной работы
Глава 4. Интегральные уравнения
§1. Основные понятия. Примеры
§2. Интегральное уравнение Абеля
§3. Решение интегральных уравнений с помощью рядов
1. Интегральное уравнение Фредгольма второго рода
2. Интегральные уравнения Вольтерра второго рода
3. Интегральное уравнение Вольтерра первого рода
§4. Связь уравнений Вольтерра с линейными обыкновенными дифференциальными уравнениями
§5. Интегральное уравнение Фредгольма второго рода с вырожденным ядром. Теоремы Фредгольма
§6. Интегральные уравнения Фредгольма второго рода с непрерывным ядром. Теоремы Фредгольма
1. Интегральные уравнения для резольвенты
2. Аналитическое продолжение резольвенты
3. Интегральное уравнение Фредгольма при любом. Характеристическое число и собственная функция ядра
4. Союзное интегральное уравнение
5. Интегральное уравнение Фредгольма в случае характеристического числа
6. Обобщение полученных результатов
§7. Симметрические интегральные уравнения
1. Основные свойства симметрических интегральных уравнений
2. Теорема Гильберта - Шмидта
3. Решение симметрических интегральных уравнений
§8. Краевые задачи на собственные значения (задача Штурма - Лиувилля)
§9. Сингулярные интегральные уравнения
1. Сингулярные интегралы
2. Сингулярные интегральные уравнения с ядром Коши
3. Сингулярные интегральные уравнения с ядром Гильберта
Задачи для самостоятельной работы
Глава 5 Дифференциальные уравнения в частных производных
§1. Дифференциальные уравнения в частных производных. Основные понятия
§2. Дифференциальные уравнения в частных производных первого порядка
1. Линейные однородные дифференциальные уравнения в частных производных
2. Задача Коши
3. Квазилинейные дифференциальные уравнения в частных производных
§3. Вывод уравнения колебаний струны. Постановка основных начально-граничных задач
§4. Вывод уравнения теплопроводности. Постановка основных начально-граничных задач
§5. Задачи, приводящиеся к уравнению Пуассона и Лапласа. Постановка основных граничных задач
§6. Понятие о корректно поставленной краевой задаче для
дифференциальных уравнений. Примеры некорректных краевых задач
§7. Задача Коши. Теорема Коши - Ковалевской
§8. Типы линейных дифференциальных уравнений в частных производных второго порядка
§9. Приведение к каноническому виду дифференциального
уравнения второго порядка от двух независимых переменных. Понятие характеристики
§10. Первая начально-граничная задача для уравнения колебаний струны
1. Постановка задачи. Единственность решения
2. Существование решения
§11. Задача Коши для уравнения колебания струны. Формула Даламбера
1. Постановка задачи Коши для уравнения струны
2. Построение общего решения уравнения струны
3. Построение решения задачи Коши
4. Физическая интерпретация решения задачи Коши
§12. Гармонические функции. Примеры. Теорема Кельвина
§13. Внутренний принцип экстремума гармонических функций. Единственность и устойчивость решения задачи Дирихле
§14. Решение задачи Дирихле для уравнения Лапласа в круге методом разделения переменных. Формула Пуассона
1. Решение задачи Дирихле а круге
2. Формула Пуассона
§15. Свойства гармонических функций
§16. Задачи Неймана и Пуанкаре для уравнения Лапласа
V Единственность решения
2. Необходимое условие разрешимости задачи Неймана
§17. Внешние граничные задачи для уравнения Лапласа
§18. Решение граничных задач для уравнения Лапласа методами потенциала и интегральных уравнений
1. Потенциалы объема, простого и двойного слоев
2. Поверхности Ляпунова
3. Свойства потенциала двойного слоя
4. Свойства потенциала простого слоя
5. Сведение задач Дирихле и Неймана для уравнения Лапласа к интегральным уравнениям
§19. Первая начально-граничная задача для уравнения теплопроводности
V Постановка задачи. Принцип экстремума. Единственность и устойчивость решения
2. Решение задачи методом разделения переменных
§20. Распространение тепла в бесконечном стержне (задача Коши)
Задачи для самостоятельной работы
Библиографический список
Список некоторых обозначений.
2-1. а) Написать граничное условие на левом конце струны, если к этому концу прикреплено колечко, которое может свободно скользить по вертикальному стержню. Массой колечка пренебречь (см. рис. 8).
б) то же, что и в 2-1 а), но колечко имеет массу ;
в) то же, что и в 2-1 б), но колечко скользит с трением.
2-2. а) Получить закон сохранения энергии струны, если на одном или на обоих концах выполнено граничное условие задачи 2-1а).
б) то же в задаче 2-1 б) (эдесь надо учесть энергию колечка);
в) то же в условиях задачи 2-1 в) (с учётом потерь на трение). 2-3. Вывести уравнение продольных упругих колебаний стержня. 2-4. Написать граничное условие на левом конце стержня, если этот конец свободен.
2-5. Написать граничное условие на левом конце стержня, если этот конец упруго закреплён (см. рис. 9).
2-6. Получить закон сохранения энергии для стержня, у которого
а) концы закреплены;
б) концы свободны;
в) один конец закреплён жестко, а другой упруго.
2-7. Вывести уравнение продольных колебаний конического стержня.
2-8. Доказать, что энергия участка струны, заключённого между точками с является невозрастающей функцией времени. Получить отсюда единственность решения задачи Коши и информацию об области зависимости для отрезка и о его области влияния.
2-9. Сформулировать и доказать закон сохранения энергии для бесконечной струны.
2-10. Нарисовать мультфильм, описывающий колебания бесконечной струны с начальными данными где при при
2-11. Описать колебания бесконечной струны, происходящие при и такие, что некоторый участок струны покоится в течение всего времени этих колебаний.
2-12. То же, что и в предыдущей задаче, но участок струны покоится при .
2-13. Нарисовать мультфильм, описывающий колебания полуограниченной струны со свободным концом (граничное условие их — см. задачу 2-1 а) и с начальными условиями график имеет форму равнобедренного треугольника с основанием
2-14. Нарисовать мультфильм, описывающий колебания полуограниченной струны с закрепленным концом и с начальными условиями где — характеристическая функция интервала (1, 31).
2-15. Получить закон сохранения энергии для полуограниченной струны с закрепленным концом.
2-16. Вдоль стержня, левый конец которого упруго закреплен, при бежит волна . Найти отражённую волну.
2-17. Вдоль бесконечной струны со скоростью движется источник гармонических колебаний частоты , т. е. .
Описать колебания струны справа и слева от источника. Найти частоты индуцированных колебаний фиксированной точки струны справа и слева от источника и дать физическую интерпретацию результата (эффект Допплера).
2-18. Описать и нарисовать стоячие волны в струне со свободными концами.
2-19. Доказать существование бесконечной серии стоячих волн в стержне, у которого один конец закреплен жестко, а другой упруго (см. задачу 2-5). Доказать ортогональность собственных функций. Найти коротковолновую асимптотику собственных значений.
2-20. На правый конец стержня при действует сила, меняющаяся по закону Написать формулу для решения и выяснить условия резонанса, если левый конец
2-21. Правый конец стержня при колеблется по закону Написать формулу для решения и выяснить условия резонанса, если левый конец
Теорема: Решение смешанной задачи для вынужденных колебаний струны:
Доказательство: Допустим, что существуют два решения u1(x,t), u2(x,t) задачи (1) – (3). Тогда разность этих решений будет удовлетворять однородному уравнению
нулевым граничным условиям
и нулевым начальным условиям
Покажем, что соотношение (4) – (6) удовлетворяет лишь функция, тождественно равная нулю.
и покажем, что при условиях (4) – (6) она не зависит от времени t. Взяв производную по t, получаем
так как внеинтегральное слагаемое обращается в нуль в силу условий (5), а , так как v(x,t) – решение уравнения (4).
Итак, , т.е. . Учитывая начальные условия (6), получаем
и, следовательно, . Из того, что интеграл от непрерывной неотрицательной функции равен нулю,
откуда , так что . В силу первого из начальных условий (6) , и значит, , т.е. .
Интеграл (7) можно переписать в виде
является кинетической энергией струны в момент времени t, а
- ее потенциальная энергия, так что функция E(t) с точностью до постоянного множителя выражает полную энергию.
Изложенный метод доказательства единственности решения смешанной задачи называется энергетическим.
Примеры:
1.
с начальными условиями
и граничными условиями
2.
Лекция 12.
Тема: Колебания круглой мембраны. Применение преобразований Лапласа к решению смешанной задачи.
Метод Фурье применяется также при изучении колебаний ограниченных тел, плоских или объемных. Рассмотрим задачу о свободных колебаниях под действием начальных возмущений однородной круглой мембраны радиуса r0 с центром в начале координат, закрепленной по краю.
Уравнение колебаний мембраны имеет вид
Введем полярные координаты . Тогда отклонение точек мембраны будет функцией полярных координат и времени . Пользуясь выражением для оператора Лапласа в полярных координатах,
запишем уравнение колебаний мембраны в виде:
(мембрана закреплена по краю) и начальным условиям
Ограничимся важным частным случаем осесемметричных колебаний, когда начальные функции f и F не зависят от . Ясно, что тогда любой момент времени t>0 величина отклонения мембраны не будет зависеть от полярного угла , а будет только функцией r и t, u=(r,t). Это означает, что при любом фиксированном t форма колеблющейся мембраны будет описываться поверхностью вращения.
При этом предположении задача сводиться к отысканию решения u=(r,t) уравнения
при граничном условии
и начальных условиях
Применяя метод разделения переменных, будем искать нетривиальные решения уравнения (4), удовлетворяющие граничному условию (5), в виде
Подставляя функцию u(r,t) в форму (7) в уравнение (4) и разделяя переменные, получим
Равенства (8) приводят к двум обыкновенным ДУ
Итак, мы пришли к задаче на собственные значения: найти те значения параметра , при которых существуют нетривиальные решения задачи (10) – (11), и отыскать эти решения.
Запишем уравнение (10) в виде:
Это дифференциальное уравнение Бесселя с . Его общее решение
Из условия следует, что с2=0 . Таким образом,
граничное условие дает
откуда следует, что число должно быть одним из нулей функции Бесселя , т.е.
где - нуль функции . Известно, что функция имеет бесконечное множество положительных нулей
откуда получаем собственные значения
и соответствующие собственные функции
При обще решение уравнения (9) имеет вид
будет решением уравнения (4), удовлетворяющему граничному условию (5).
Решение u(x,r) исходной задачи (4) – (6) ищем в виде формального ряда
Если подставив an и bn в (12), ряд сходится равномерно, то мы поучаем решение задачи (4) – (6).
Применение преобразований Лапласа к решению смешанной задачи.
Пусть требуется найти решение u(x,t) уравнения
удовлетворяющее начальным условиям
и граничными условиями
Применяя преобразование Лапласа по t, предположим, что , и , рассматриваемые как функции t, являются функциями-оригиналами. Пусть U(x,p) есть изображение функции по Лапласу,
Так как операция дифференцирования по х и операция интегрирования по t в преобразовании Лапласа перестановочны, получим
(здесь величина р рассматривается как параметр, и вместо частных производных пишут обычные ).
По правилу дифференцирования оригиналов имеем
Отсюда, учитывая начальные условия (2), получаем
Пусть тогда граничные условия дают
Переходя к изображениям, сводим задачу (1) – (3) для уравнения с частными производными к граничной задаче для обыкновенного ДУ:
найти решение U(x,p) уравнения
при граничных условиях
Пусть U(x,p) - решение задачи (4) – (5). Тогда функция u(x,t) (оригинал для U(x,p))будет решением исходной задачи (1) – (3).
Пример: Струна l закреплена на концах x=0, x=l. Начальные отклонения струны определяются формулой . Начальные скорости отсутствуют. Найти отклонение u(x,t) струны при t>0.
Решение: Задача сводиться к решению уравнения
при начальных условиях
и граничных условиях .
Применим преобразование Лапласа. По правилу дифференцирования с учетом начальных условий получим
Струной будем называть тонкую туго натянутую упругую нить.
При построени математической модели колебаний струны будем рассматривать малые колебания, происходящие в одной и той же плоскости. Пусть в состояниии покоя струна расположена вдоль оси Ox на отрезке [0,l] и при колебании каждая точка перемещается перпендикулярно оси (поперечные колебания). Тогда отклонение любой точки струны в произвольный момент времени U есть функция U(x,t) (см. рис.2).
Предположим, что натяжение столь велико, что силой тяжести и сопротивлением при изгибе можно пренебречь. Кроме того, в силу малости колебаний, будем пренебрегать также величинами высшего порядка малости по сравнению с производной Ux.
Выделим малый участок струны (см. рис.3) и рассмотрим силы, действующие на него. Так как струна не сопротивляется изгибу, то ее натяжение направлено по касательной к струне в точке x. Более того, в рамках наших предположений можно считать величину силы натяжения постоянной. В самом деле, длина любого участка струны (величиной Ux 2 можно пренебречь). С ледовательно, в соответствии с законом Гука .
Пусть ρ ( x )- линейная плотность в точке x , а γ ( x , t )- плотность внешних сил, действующих на струну в момент времени t, и направленных перпендикулярно Ox .
Результирующая сила, действующая на участок струны [ x , x +∆ x ] в направлении перпендикулярном оси OX , равна (см. рис. 3)
.
При выводе этой формулы учитываем, что при малых колебаниях
По второму закону Ньютона произведение массы на ускорение равно действующей силе mw = F , где w=Utt, поэтому
ρ ∆ xUtt = T 0[ Ux ( x + ∆ x , t )- Ux ( x , t )]+ γ ( x , t ) ∆ x .
Разделим обе части равенства на Δx и устремим Δx к нулю:
ρ ( x ) Utt = T 0[ Ux ( x + ∆ x , t )- Ux ( x , t )]/ ∆ x + γ ( x , t ) .
Это уравнение называется уравнением вынужденных колебаний струны. Если струна однородная, то есть ρ ( x )= const , то уравнение (3) обычно записывают в виде
Utt = a 2 Uxx + f ( x , t ),где a 2 = T 0/ ρ ; f ( x , t )= γ ( x , t ) / ρ .
В том случае, когда на струну не действуют внешние силы, получается уравнение свободных колебаний струны
Уравнения (3) и (4) являются одномерными волновыми уравнениями (соответственно, неоднородным и однородным).
Волновыми эти уравнения называются потому, что они описывают распространение слабых возмущений в упругой среде (т.е. механические колебания с малыми амплитудами), которые в физике называют волнами. Волновые уравнения возникают также в задачах об электрических колебаниях, в гидродинамике и акустике, в теории упругости, при изучении электромагнитных полей.
Начальные условия и граничные условия.
Дифференциальные уравнения с частными производными, вообще говоря, имеют бесчисленное множество решений. Чтобы из этого множества выбрать то единственное решение, которое соответствует реальному физическому процессу (например, колебанию данной струны), надо задать некоторые дополнительные условия. В теории уравнений с частными производными, как и в обыкновенных дифференциальных уравнениях, задаются условия, называемые начальными и краевыми (граничными) условиями. Начальные условия в математической физике соответствуют состоянию физического процесса в начальный момент времени, который обычно принимают за t=0. В результате возникает задача Коши. Однако здесь есть некоторые отличия. Во-первых, начальные условия задаются для нестационарных уравнений, то есть таких уравнений, которые описывают нестационарные (зависящие от времени) процессы. Такими уравнениями являются, к примеру, волновые уравнения и уравнения теплопроводности. Во-вторых, задача Коши для уравнений с частными производными имеет единственное решение только в том случае, когда соответствующее уравнение рассматривается или на всей прямой, или на всей плоскости, или во всем пространстве. Например, это может быть задача о колебании бесконечной струны или о распространении тепла в бесконечном стержне. На практике к таким задачам приходят в том случае, когда имеется очень длинная струна или очень длинный стержень и интересуются процессами, происходящими далеко от концов, а влиянием концов пренебрегают. Если взять, допустим, длинный провод и слегка качнуть его в середине, то по нему влево и вправо побегут волны. Картина начнет искажаться только тогда, когда волны дойдут до концов провода и, отразившись, пойдут обратно. Следовательно, не учитывая влияния концов, мы тем самым не будем учитывать влияния отраженных волн.
Для волнового уравнения Utt = a 2 Uxx задаются два начальных условия U | t =0 = φ ( x ), Ut | t =0 = ψ ( x ). Иногда их записывают иначе: U ( x , 0) = φ (х), Ut ( x , 0) = ψ (х). Первое условие физически задает начальную форму струны (начальные отклонения точек струны), а второе условие - начальные скорости точек струны. В случае волнового уравнения Utt = a 2 Δ U на плоскости или в пространстве задаются те же два начальных условия, только функции φ и ψ , соответственно, будут зависеть от двух или трех переменных.
Если размеры струны или стержня не очень велики и влиянием концов нельзя пренебречь, то в этих случаях одни начальные условия уже не обеспечивают единственность решения задачи. Тогда необходимо задавать условия на концах. Они называются граничными условиями или краевыми условиями.Для уравнения колебаний струны часто задаются условия U | x =0 = 0, U | x = l = 0. Иначе их записывают еще и гак: U (0, t )=0, U ( l , t ) = 0. Эти условия физически означают, что концы струны закреплены (то есть отклонения при х = 0 и при х = l в любой момент времени равны нулю). Можно задавать и другие условия на концах струны, например, Ux |х=0= 0 , Ux |х= l = 0. Такие условия возникают в следующей задаче.
Пусть концы сруны перемещаются вдоль вертикальных направляющих без трения (см. рис.4).
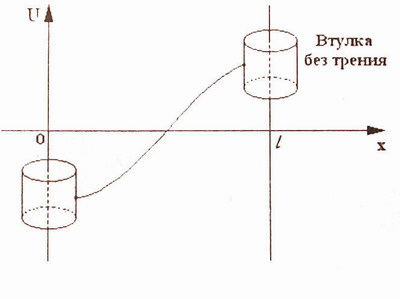
рис.4
Так как вертикальные силы, действующие на левый и правый концы струны, определяютя выражениями T 0 Ux ( O , t ) и T 0 Ux (l, t ) (см рис. 2), то записанные выше условия означают, что на концы струны не действуют никакие силы(поэтому такие условия называют еще условиями свободных концов).
Как было уже сказано, волновое уравнение Utt = a 2 Uxx описывает не только колебания струны, но и другие волновые процессы, к примеру, продольные колебания пружины, продольные колебания стержня, крутильные колебания вала. В этих задачах возникают граничные условия и других видов. Подробно такие задачи мы изучать не будем. Однако приведем основные типы граничных условий. Обычно рассматривают три типа:
Граничные условия (5), (6) и (7) называются однородными, если правые части g1(t) и g2(t) тождественно равны нулю при всех значениях t. Если хотя бы одна из функций в правых частях не равна нулю, то граничные условия называются неоднородными.
Аналогично формулируются граничные условия и в случае трех или четырех переменных при условии, что одна из этих переменных - время. Г раницей в этих случаях будет или замкнутая кривая Г, ограничивающая некоторую плоскую область, или замкнутая поверхность Ω, ограничивающая область в пространстве. Соответственно изменится и производная от функции, фигурирующая в граничных условиях второго и третьего рода. Это будет производная по нормали n к кривой Г на плоскости или к поверхности Ω в пространстве, причем, как правило, рассматривают нормаль, внешнюю по отношению к области(см.рис. 5 ) .
К примеру, граничное условие (однородное) первого рода на плоскости записывается в виде U|Γ=О, в пространстве U|Ω=0. Граничное условие второго рода на плоскости имеет вид ,а в пространстве . Конечно, физический смысл этих условий разный для различных задач.
При постановке начальных и граничных условий возникает задача об отыскании решения дифференциального уравнения, удолетворяющего заданным начальным и граничным (краевым) условиям. Для волнового уравнения (3) или (4), начальных условий U(x,0)= φ(x), Ut (x,0)=ψ(x) и в случае граничных условий первого рода (5), задача называется первой начально-краевой задачей для волнового уравнения. Если вместо граничных условий первого рода задавать условия второго рода (6) или третьего рода (7), то задача будет называться, соответственно, второй и третьей начально-краевой задачей. Если граничные условия на разных участках границы имеют различные типы, то такие начально-краевые задачи называют смешанными.
Читайте также:

