Движение по окружности реферат

Обновлено: 30.06.2024

Формула (1.18) связывает величины угловой и линейной скоростей. Соотношение, связывающее векторы щ и v, следует из рис. А именно, вектор линейной скорости представляет собой векторное произведение вектора угловой скорости и радиуса-вектора точки r: Пройденный путь S, перемещение dr, скорость v, тангенциальное и нормальное ускорение at, и an, представляют собой линейные величины. Для описания… Читать ещё >

Равномерное движение по окружности ( реферат , курсовая , диплом , контрольная )

Пройденный путь S, перемещение dr, скорость v, тангенциальное и нормальное ускорение a_t, и a_n, представляют собой линейные величины. Для описания криволинейного движения наряду с ними можно пользоваться угловыми величинами.

Рассмотрим более подробно важный и часто встречаемый случай движения по окружности. В этом случае наряду с длиной дуги окружности движение можно характеризовать утлом поворота ц вокруг оси вращения. Величину.

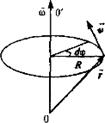
называют угловой скоростью. Угловая скорость представляет собой вектор, направление которого связывают с направлением оси вращения тела (рис.).

Обратим внимание на то, что, в то время как сам угол поворота ц является скаляром, бесконечно малый поворот dц — векторная величина, направление которой определяется по правилу правой руки, или буравчика, и связано с осью вращения. Если вращение является равномерным, то щ=const и точка на окружности поворачивается на равные углы вокруг оси вращения за равные времена. Время, за которое она совершает полный оборот, т. е. поворачивается на угол 2р, называется периодом движения Т. Выражение (1.15) можно проинтегрировать в пределах от нуля до Т и получить угловую частоту

Число оборотов в единицу времени есть величина, обратная периоду, — циклическая частота вращения.

Нетрудно получить связь между угловой и линейной скоростью точки. При движении по окружности элемент дуги связан с бесконечно малым поворотом соотношением dS = R· dц. Подставив его в (1.15), находим.

Таким образом, вектор угловой скорости направлен по оси вращения точки и определяется по правилу правой руки или буравчика.

Угловое ускорение — производная по времени от вектора угловой скорости щ (соответственно вторая производная по времени от угла поворота).

Выразим тангенциальное и нормальное ускорение через угловые скорости и ускорение. Используя связь (1.18),(1.12) и (1.13), получаем ("https://referat.bookap.info", 25).

Таким образом, для полного ускорения имеем.

Величина в играет роль тангенциального ускорения: если в = 0. полное ускорение при вращении точки не равно нулю, a =R· щ 2 ? 0.

44. Связь линейных и угловых параметров При рассмотрении поступательного движения мат. точки мы рассмотрим линейные параметры:

S (перемещение) — расстояние от точки до конечной точки.

vскорость с которой двигаются тела аускорение Эти три величины связаны между собой :

При рассмотрении вращательного движения мат. точки мы рассмотрим угловые параметры:

E — угловое ускорение Они так же связаны между собой:

В тоже время линейные параметры можно связать с угловыми параметрами:

А именно, вектор линейной скорости представляет собой векторное произведение вектора угловой скорости и радиуса-вектора точки r:

Движение по окружности - простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории - предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости - радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → - v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → - v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → - радиус вектор точки на окружности с началом в ее центре.

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов - нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 - v 1 - изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

1. Криволинейное движение. Перемещение, скорость и ускорение при криволинейном движении.

2. Движение по окружности. Угол поворота, радиан. Решение задач.

3. Угловая и линейная скорости при равномерном движении по окружности. Решение задач.

4. Ускорение при равномерном движении тела по окружности.

5. Об относительности движения тела при вращении системы отсчета.

6. Обобщающее повторение. Решение задач.

Из курса физики VI класса учащиеся знают, что движение, траекторией которого является кривая линия, называется криволинейным движением. В VIII классе эти знания дополняются и углубляются.

Приводим примеры криволинейного движения (движение тела, брошенного под углом к горизонту; вращение Земли вокруг солнца, движение искусственных спутников вокруг Земли, движение заряда, вылетевшего из орудия и др.)

Демонстрируем некоторые опыты: выстрел из баллистического столета, движение шарика на центробежной дороге, изменение направления движения стального шарика под действием магнита.

Учащиеся знают, что в случае прямолинейного движения траектория — прямая линия и поэтому положение любой точки траектории определяется одной координатой. В случае криволинейного движения, происходящего на плоскости, изменяются две координаты х и у.

После этого выясняем, как изменяется скорость в криволинейном движении, даем понятие о направлении скорости и перемещения в криволинейном движении. Важно объяснение этого материала иллюстрировать опытом, показывающим, что вектор скорости точки направлен по касательной к траектории движения. Рекомендуем на уроке показать следующую демонстрацию.

На центробежной машине укрепляется вертикально фанерный круг диаметром 18—20 см. Нижняя его часть (сегмент) погружается в сосуд с подкрашенной водой (можно использовать сосуд от прибора по теплоемкости) (Рис. 1). При вращении круга центробежной машины струи воды летят по направлениям касательных к кругу.

Эти опыты помогают учащимся сделать вывод: направление скорости криволинейного движения определяется направлением касательной в той точке траектории, в которой находится в данный момент вращения движущаяся материальная точка . Абсолютное значение скорости в криволинейном движении измеряется отношением пути, пройденного материальной точкой за известный промежуток времени, к значению этого промежутка времени. Длина пути в этом случае отсчитывается по дуге, вдоль траектории движения. (Для учителя напомним, что при изучении криволинейного движения точки в механике пользуются понятиями тангенциального и нормального ускорения и полного ускорения.)

Так как направление касательной к траектории в разных точках различно, то это означает, что в криволинейном движении в общем случае скорость изменяется по направлению .

При изучении криволинейного движения особое значение приобретает мгновенная скорость . Обращаем внимание и на следующий факт. В криволинейном движении вектор скорости не совпадает по направлению с вектором перемещения, а составляет с ним некоторый угол. В прямолинейном же движении направления этих векторов совпадают или противоположны.

По определению линейная скорость .

Другими величинами, характеризующими движение точки по окружности, являются угол поворота и угловая скорость.

При рассмотрении понятий линейной и угловой скорости можно применить самодельный прибор (Рис. 2). Прибор изготовляют из фанеры, устройство его ясно из рисунка. Различие линейной и угловой скоростей демонстрируется так: совмещают неподвижный радиус ОА с подвижным радиусом ОА₁ , затем медленно и равномерно поворачивают на некоторый угол и показывают криволинейную траекторию движения точки А – дугу АА₁ Сообщают, что отношение длины этой дуги > времени и дает линейную скорость точки А. Затем повторяют демонстрацию и обращают внимание учащихся на длину путей точек А, В и С, по-разному удаленных от оси вращения. Делают вывод о разном значении линейных скоростей этих точек. Равномерно вращая диск и обращая внимание на изменение угла поворота подвижного радиуса относительно неподвижного, можно дать понятие об угловой скорости. Медленнее и более быстрое движение диска проиллюстрирует движение с меньшей и большей угловыми скоростями. Наконец, если равномерно вращать диск так, чтобы он поворачивался за 1 с (по метроному) на угол в один радиан, можно дать понятие об единице угловой скорости — 1 рад/с.

Для закрепления знаний формул линейной и угловой можно предложить учащимся и такую задачу:

Найти угловую и линейную скорости искусственного спутника Земли, вращающегося по круговой орбите с периодом вращения Т=88 мин, если известно, что его орбита расположена на расстоянии 200 км от поверхности Земли в плоскости экватора.

В школьных учебниках физики для вывода формулы центростремительного ускорения чаще всего используют способ, основанный на предельном переходе. Однако ввиду отсутствия знаний у учащихся VIII класса о предельном переходе в курсе школьной механики он является нестрогим и трудно усваивается учащимися. Поэтому наиболее продуктивно использовать следующий подход. Вначале следует обратить внимание на то обстоятельство, что при равномерном движении материальной точки по окружности вектор скорости непрерывно изменяется по направлению. Следовательно, за промежуток времени происходит некоторое изменение скорости . Таким образом, v ~t . В этом случае движения возникает ускорение .

Важно заметить, что здесь речь идет об ускорении в точке окружности, а значит промежуток времени берется достаточно малым. Чтобы определить направление вектора а, его модуль |а|, например, в точке А окружности (Рис. 3), ццелесообразно воспользоваться свойством двух векторов, имеющих равные модули и образующих малый угол, и зависимостью между линейной и угловой скоростями.

Пусть за очень малый промежуток времени тело переместилось из точки А в точку В (см. Рис. 3). Тогда изменение вектора скорости . Следовательно, для определения достаточно к вектору прибавить вектор . Из рисунка видно, что вектор , равный разности, направлен в сторону кривизны окружности в точке А . По свойству векторов модуль разности двух равных векторов, образующих малый угол , равен произведению модуля вектора на угол, т. е. . Кроме того, в этом случае вектор должен быть перпендикулярен вектору (так как между векторами и угол мал). Вектор скорости (как и ) направлен по Касательной, а касательная перпендикулярна радиусу. Отсюда следует, что вектор должен быть направлен по радиусу окружности, и направлен к ее центру. Из формулы - следует, что вектор ускорения имеет такое же направление, что и вектор (так как время – скалярная величина). Таким образом, учащиеся подводятся к выводу: вектор ускорения, возникающего при равномерном движении окружности тела или точки, всегда направлен по радиусу к центру окружности . Поэтому такое ускорение называется центростремительным.

Далее находят модуль центростремительного ускорения .

Необходимо обратить внимание учащихся еще на следующий факт. Так как |v | и R — постоянные величины, то модуль при равномерном движении тела по окружности остается все время неизменным. Однако отсюда еще нельзя сделать заключение, что такое движение равноускоренное. Так как в процессе равномерного движения тела по окружности вектор ускорения направлен по радиусу к центру, то непрерывно изменяется его направление. Таким образом, равномерное движение тела (точки) по окружности есть движение с переменным ускорением; оно не является равноускоренным.

Формирование основных понятий вращательного движения, как составной части криволинейного движения, является довольно трудной для усвоения темой. Она нуждается во множестве примеров и демонстраций, вполне возможных для проведения на уроке. Полученные знания будут находить применение в последующих темах изучения физики. Ученик, свободно оперирующий понятиями вращательного движения, подготовлен к изучению динамики вращательного движения. Также знание понятий будет использоваться в теме колебаний. Следуя этапам, рекомендованным в данной работе, можно в достаточной степени закрепить у учащихся средней школы понимание рассматриваемых понятий, необходимое для дальнейшего изучения физики, формирования навыков решения задач кинематики вращательного движения, понимания использования данных понятий в быту.

Движение по окружности - простейший пример криволинейного движения. Скорость движения по окружности называется линейной скоростью. При равномерном движении по окружности модуль мгновенной скорости материальной точки с течением времени не изменяется. Движущаяся точка за равные промежутки времени проходит равные по длине дуги окружности.
Изменение положения точки на окружностихарактеризуется изменением угловой координаты точки. Угол называется углом поворота радиус - вектора точки.
При равномерном движении точки по окружности за любые равные промежутки времени углы поворота ее радиус-вектора одинаковы. Поэтому угловой скоростью движения точки по окружности вокруг заданного центра называется отношение угла поворота радиус-вектора точки за промежуток, времени к длительности этого промежутка.Промежуток времени , в течение которого точка совершает один полный оборот по окружности, называется периодом обращения (периодом вращения), а величина обратная периоду - частотой обращения. Единица частоты - секунда в минус первой степени.
Путь пройденный точкой за один период по окружности радиуса равен , а угол поворота радиус-вектора точки за тот же промежуток времени равен т.е. исвязь между линейной и угловой скоростью.
Изменение вектора скорости по направлению характеризуется центростремительным ускорением . В каждой точке траектории вектор центростремительного ускорения направлен по радиусу к центру окружностиа его модуль равен.
Среди различных видов криволинейного движения особый интерес представляет равномерное движение тела по окружности. Это самый простой видкриволинейного движения. Вместе с тем любое сложное криволинейное движение тела на достаточно малом участке его траектории можно приближенно рассматривать как равномерное движение по окружности.

Центростремительное ускорение. При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости изменяется в процессе движения. Определим ускорение тела, движущегося равномернопо окружности радиусом R. За интервал времени Δt тело проходит путь .
Этот путь Δs равен длине дуги АВ Среди различных видов криволинейного движения особый интерес представляет равномерное движение тела по окружности. Это самый простой вид криволинейного движения. Вместе с тем любое сложное криволинейное движение тела на достаточно малом участке его траектории можно приближенно рассматривать какравномерное движение по окружности.

Центростремительное ускорение. При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости изменяется в процессе движения. Определим ускорение тела, движущегося равномерно по окружности радиусом R. За интервал времени Δt тело проходит путь .
Этот путь Δs равен длине дуги АВ (рис. 17). Векторы скоростей и точкахА и В направлены по касательным к окружности в этих точках, угол α между векторами и равен углу между радиусами ОА и OB.

Для нахождения вектора ускорения нужно найти разность векторов скорости и определить отношение изменения скорости к малому интервалу времени Δt, за который произошло это изменение:

Из подобия треугольников ОАВ и BCD следует

Если интервал времениΔt мал, то мал и угол α. При малых значениях угла α длина хорды АВ примерно равна длине дуги АВ, т. е. . Так как , и , то из выражения (3.1) получаем

из выражений (3.3) и (3.4) получаем

Из рисунка 17 видно, что, чем меньше угол α, тем ближе направление вектора к направлению на центр окружности. Так как вектор ускорения равенотношению вектора к интервалу времени Δt при условии, что интервал времени Δt очень мал, то вектор ускорения при равномерном движении по окружности направлен к ее центру.

При изменении положения тела на окружности меняется направление на центр окружности. Следовательно, при равномерном движении тела по окружности модуль ускорения имеет постоянное значение, но.

Исследование равномерного движения точки с заданной массой с угловой скоростью по окружности на двух шарнирно связанных невесомых стержнях. Расчет элементарной функции радиальной силы, действующей на элемент трубки тора с заданной массой и длиной.

Рубрика	Физика и энергетика
Вид	статья
Язык	русский
Дата добавления	04.03.2018
Размер файла	357,1 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Движение по окружности

Берников Василий Русланович,

инженер, г. Нижний Новгород.

Рассмотрим равномерное движение точки В массой m с угловой скоростью w_о по окружности на двух шарнирно связанных невесомых стержнях ОА и АВ (рис.1).

Рис. 1.

Если длина стержня АВ 2 ; Y=90°, тогда

Теперь вычислим радиальную силу для жидкости (рис. 5). Пусть положительное ускорение начинается с приложением силы в начале полуокружности.

Рис. 5.

движение окружность скорость радиальный

Запишем элементарную функцию радиальной силы, действующей на элемент трубки тора массой ?m и длиной ??:

?Fр = (1/2)?mwsin(?Y). (1.2)

Масса элемента равна плотности потока, умноженной на его объём

?m = с ?V. (1.3)

Длина половины тора по средней линии

где р - число пи.

Объём половины тора

V = р 2 Rr 2 = рR р r 2 = ? р r 2 ,

где r - радиус трубки тора.

Для элементарного объёма запишем

?V = ?? р r 2 .

Известно, что для окружности

?? = R?Ш,

?V = р r 2 R?Ш. (1.4)

Подставим выражение (1.4) в (1.3) получим:

?m = с р r 2 R?Ш. (1.5)

Теперь подставим (1.5) в (1.2), тогда

?Fр = (1/2)с р r 2 R wsin(?Y)?Ш. (1.6)

Радиальная сила, действующая в перпендикулярном диаметру полуокружности направлении на один элемент (рис. 5)

?Fр^ = ?FрsinY= (1/2)с р r 2 R wsinYsin(?Y)?Ш. (1.7)

Рис. 6.

Так как в жидкости действует сила инерции от каждого элемента на соседний, то необходимо учесть их радиальную составляющую (рис.6)

?Fри = ?mwsin(?Y/2). (1.8)

?Fри - это радиальная сила инерции, которая действует с последнего элемента на предыдущий. Если количество элементов n, то на k-й элемент действует радиальная сила инерции (n-k)?Fри. Радиальная сила инерции, действующая в перпендикулярном диаметру полуокружности направлении на один элемент

?Fри = (n-k)?mwsin(?Y/2)sinY = (n-k)с р r 2 Rwsin(?Y/2)sinY?Ш. (1.9)

Итак, общая радиальная сила, действующая в перпендикулярном диаметру полуокружности направлении на один элемент будет

?Fk^ = с р r 2 R wsinY[(1/2)sin(?Y) + (n-k)sin(?Y/2)]?Ш. (1.10)

Уравнение (1.10) решаем приближённым методом для 11 элементов.

Пусть w=5м/с 2 ; r=0,02м; с=1000кг/м 3 ; R=0,2м; n=11; ?Y=18°; Y=(0°,18°,36°,…,180°), тогда общая радиальная сила, действующая в перпендикулярном диаметру полуокружности направлении будет

Если положительное ускорение циркулирующей среды начинается с приложением силы из конца полуокружности, тогда проекция радиальной силы будет действовать в обратном направлении.

Для системы, циркулирующая среда, в которой движется с замедлением по окружности с замедляющей силой в конце циркулирующей среды радиальная сила имеет такое же направление как на рис.5, а с замедляющей силой в начале циркулирующей среды в обратную сторону.

Для системы, циркулирующая среда, в которой движется равномерно по окружности радиальная сила отсутствует.

2. Сивухин Д. В. Общий курс физики. Т.1. Механика. 5-е изд., стереот. - М.: ФИЗМАТЛИТ., 2010, 560с.

3. Хайкин С.Э. Физические основы механики, М.: Наука, 1971, 752с.

Подобные документы

Использование математических методов для определения основных физических величин моделей реальных материальных объектов. Расчет силы реакции в стержнях, угловой скорости кривошипа, нагрузки на опоры балки; построение графика движения материальной точки.

контрольная работа [1,5 M], добавлен 02.12.2010

Поиск эффективных методов преподавания теории вращательного движения в профильных классах с углубленным изучением физики. Изучение движения материальной точки по окружности. Понятие динамики вращательного движения твердого тела вокруг неподвижной оси.

курсовая работа [1,7 M], добавлен 04.05.2011

Изучение законов Ньютона, лежащих в основе классической механики и позволяющих записать уравнения движения для любой механической системы. Анализ причин изменения движения тел. Исследование инерциальных систем отсчета. Взаимодействие тел с разной массой.

презентация [531,3 K], добавлен 08.11.2013

Механическое движение. Ускорение при движении по окружности. Основы динамики. Силы упругости. Закон Гука, трение. Гравитационное взаимодействие. Условие равновесия тел. Закон сохранения импульса, энергии в механике. Архимедова сила для жидкостей и газов.

реферат [160,9 K], добавлен 15.02.2016

Определение скорости, нормального, касательного и полного ускорения заданной точки механизма в определенный момент времени. Расчет параметров вращения вертикального вала. Рассмотрение заданной механической системы и расчет скорости ее основных элементов.

контрольная работа [2,4 M], добавлен 13.03.2014

Движение центра масс механической системы. Количество движения точки и импульс силы. Теорема об изменении количества движения механической системы. Движение точки под действием центральной силы. Закон сохранения кинетического момента механической системы.

презентация [533,7 K], добавлен 09.11.2013

Измерение угловой скорости в Международной Системе СИ. Формула расчета максимальной высоты полета. Движение свободного падания. Понятие и алгоритм расчета центростремительного ускорения. Измерение радиуса окружности. Обозначение начальной координаты.

Читайте также: