Циклоида загадка математики и природы реферат
Обновлено: 02.07.2024
Эта обычная, казалось бы, кривая линия стала одним из "точильных камней", зарождавшегося в 18 веке математического анализа. Обладая множеством интересных свойств, циклоида широко применяется в науке и технике. Узнаем подробнее. Поехали!
Что такое циклоида ?
На самом деле, когда математики позднего средневековья начали изучать циклоиду, то были немного сокрушены тем фактом , что их предшественники не замечали лежащую буквально под их ногами замечательную кривую (об этом писал, в частности, Блез Паскаль).
Действительно, ведь циклоиду видел абсолютно каждый из Вас: это всего лишь траектория движения точки катящегося колеса! Смотрите:
Описывается циклоида достаточно сложным уравнением (размещу его здесь, но дальше сложной математики не будет):
Зачем я привел эту формулу? Я хочу обратить Ваше внимание, каким образом записывается уравнение циклоиды.
Зачем я привел эту формулу? Я хочу обратить Ваше внимание, каким образом записывается уравнение циклоиды.
В школьном курсе математики привычная запись функции имеет вид y= f(x) (или наоборот) . Более важно то, что под f(x) чаще всего понимается многочлен , т.е. конструкция, в которой есть операции умножения, сложения, вычитания и возведения в степень (в т.ч. в виде извлечения корня).
Так вот, циклоида является первой из исследованных математиками кривых, которая не может быть записана в виде многочлена (привет, арккосинус!). Такие кривые называют трансцендентными, в отличие от более простых алгебраических.
Впервые циклоиду заметили в начале 16 века, но современное название этой кривой дал Галилео Галилей. Он же экспериментально открыл тот факт, что каждая "арка" циклоиды по площади втрое больше исходного "колеса" . Но есть другое свойство циклоиды, еще более удивительное!
Таутохронность циклоиды
Это свойство заключается в том, что одно и то же тело, помещенное в любую точку перевернутой циклоиды достигнет конечной точки за одинаковое время . Вот так это происходит:
Кроме того, перевернутая циклоида называется кривой скорейшего спуска или брахистохроной.
Есть еще и вот такое наглядное доказательство с маятником:
Циклоида широко применяется в самых неожиданных местах. Например, рампы для скейтбордистов выполняются именно в такой форме, чтобы увеличить максимальные скорости спортсменов. Рассматриваются возможности применения циклоидальных траекторий в космических перелетах , что позволит очень сильно снизить необходимую массу корабля, за счет большой инерции, получаемой при полете по такой кривой.
Рассказ про применение циклоид в технике будет неполным без упоминания эпициклоид и гипоциклоид и их разновидностей. Но эту историю, с Вашего позволения, я расскажу позже. Спасибо за внимание!
Пока что предлагаю ознакомиться с моим материалом про три очень красивых и важных графика функций.
Подписывайтесь на канал в Яндекс. Дзен или на канал в телеграм "Математика не для всех" , чтобы не пропустить интересующие Вас материалы.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Как создать электронную книгу
ученик 6 класса
Руководитель:
г. Бадаримнск, 2017 г
В природе существует много интересного, загадочного, которого мы еще не знаем. И человек старается их каким-то образом разгадать, найти ответы на возникшие вопросы в книгах, энциклопедиях, а сейчас и в интернете.
Цель: Познакомиться с основными свойствами циклоиды (кривой второго порядка) и проявлениями ее в жизни.
Задачи: - изучить литературу по теме исследования;
- пополнить знания о разновидностях циклоиды и их свойствах;
- узнать о значении и применении циклоиды в жизни, окружающем мире, быту.
Основная часть
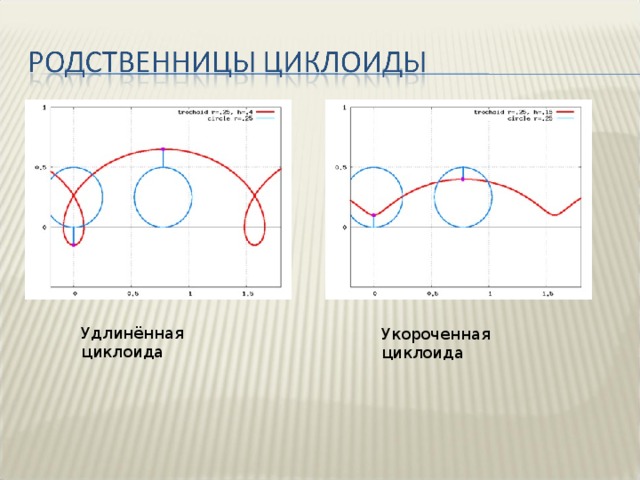
Что же такое циклоида: сделали модель колеса (круг), зафиксировали неподвижную точку М на круге и стали катить по неподвижной прямой, по окружности без скольжения. Эта точка стала описывать кривую, которая называется циклоидой. Циклоида – плоская кривая, которую описывает фиксированная точка М, неподвижно связанная с окружностью, катящейся по неподвижной прямой. Если точка М расположена на окружности, то получим линию m– обычную циклоиду (рис. 1), если же вне окружности (N), то удлиненную циклоиду – n (рис. 2),если же внутри окружности (K), то укороченную циклоиду – k(рис. 3) (В переводе с греческого: -кругообразный, от - круг, -вид).

Рис. 1. Циклоида обычная

Рис. 2. Циклоида удлиненная

Рис. 3. Циклоида укороченная
Кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности вне ее, называется эпициклоидой (рис. 4).

Рис. 4. Эпициклоида
Если радиус неподвижной окружности равен радиусу подвижной, то
эпициклоиду называют кардиоидой (рис. 5).
Рис. 5. Кардиоида
Плоская кривая, описываемая точкой окружности внутри нее, называется
гипоциклоидой (рис.6).
В зависимости от соотношения длин радиусов подвижной и неподвижной окружностей, получаются различные формы гипоциклоид. Если радиус неподвижной окружности в 4 раза больше радиуса подвижной, то эта гипоциклоида называется астроидой (рис. 7).
Из истории открытия циклоиды
Свойства циклоиды
Кривая – циклоида – периодическая (Т=2 R), то есть повторяется через определенный промежуток.

Рис. 7. Периодичность циклоиды
Касательная прямая — прямая, проходящая, через точку кривой и совпадающая с ней в этой точке.
Нормаль — это прямая, перпендикулярная касательной прямой к некоторой кривой.
Сравнивая вес двух металлических пластинок равной толщины, одна из которых вырезана по циклоиде, а другая по окружности, порождающей эту циклоиду, Галилей обнаружил, что площадь сегмента циклоиды в три раза больше площади соответствующего круга, а длина дуги арки равна четырем диаметрам круга.
Юный Галилей пытался экспериментально проверить свою догадку о том, что свободное падение – равноускоренное движение. И он перенес наблюдения с Пизанской башни в лаборатории. Опыты Галилея дали толчок строгим математическим исследованиям циклоиды. Сначала его ученик Торричелли, а затем Роберваль, Декарт и Ферма не только обосновали зависимость, открытый Галилеем, но установили ряд
других свойств циклоиды. Простота и изящество определения циклоиды привели к ней многих ученых-математиков XVII–XVIIIвв. Ею занимались Паскаль, Лейбниц, Гюйгенс, Даниил Бернулли. Причем вначале циклоида сама была предметом пристального изучения, а впоследствии на ней проверялись методы зарождающегося математического анализа.
Перевернем циклоиду выпуклостью вниз и представим, что по ней скатывается тяжелая частица (рис. 7). Из какой бы точки циклоиды ни начинала движение частица, она скатится вниз за одно и то же время.
т. е. такой маятник, период колебаний которого не зависит от его размаха.Христиан ГЮЙГЕНС, голландский ученый, в 1657 году создал такой маятник.

Рис.8. Изохронность циклоиды
В 1696 г. Даниил Бернулли открыл еще одно замечательное свойство этой кривой.

Рис. 9. Брахистохронность циклоиды
Из истории решения шести задач о циклоиде
Парадоксы странные, но истинные
Если мы заставим первую монету катиться по второй так, чтобы она прошла ровно половину окружности (как указано стрелкой), мы можем ожидать, что, придя к точке, диаметрально противоположной первоначальной, монета перевернется вниз головой по сравнению с исходной позицией. Мы убеждены, что, пройдя половину окружности, монета должна повернуться на 180°. Проведя этот эксперимент с реальной монетой, мы убедились, что она окажется снова в исходном положении — будто бы она прошла полную окружность, а не ее половину (рис. 8).
Рис . 8. Парадокс с монетами
Применение циклоиды
Циклоида имеет огромное практическое применение не только в математике (испытывали силу новых мощных математических методов и приемов исследования кривых линий (дифференциальное и интегральное исчисление)), но и в технологических расчетах, в физике (задача о брахистохроне привела к изобретению вариационного счисления). Циклоида так же находит себе применение в технике (в зубчатом зацеплении, при котором профили зубьев имеют очертания циклоидальных кривых) и теории механизмов (рис. 10)
Рис. 10. Применение зубчатых зацеплений в технике.
Задачи, приводящие к циклоиде, сыграли огромную роль в становлении механики и математического анализа. Но, когда величественные здания этих наук были построены, оказалось, что эти задачи являются частными, далеко не самыми важными. История циклоиды завершилась в конце XVII века: стало ясно, что циклоида не связана с фундаментальными законами природы, как например, конические сечения. Произошла поучительная историческая иллюзия.
В ходе работы над докладом были выяснены основные свойства циклоиды. Смогли построить циклоиду с помощью модели. Как оказалось циклоида имеет огромное практическое применение не только в математике, но и в технологических расчетах, физике, технике. Циклоида оказалась неразрывно связанной с одним из самых интересных периодов в истории математики.

Циклоида определяется кинематически как траектория фиксированной точки производящей окружности радиуса r, катящейся без скольжения по прямой.

Циклоида – периодическая кривая. Из определения циклоиды следует, что основание арки циклоиды равно длине производящей окружности, т.е. 2 π r .
Блез Паскаль писал о циклоиде:

Касательная прямая — прямая, проходящая через точку кривой и совпадающая с ней в этой точке.
Нормаль — это прямая, перпендикулярная касательной прямой к некоторой кривой.

- плоская кривая, образуемая фиксированной точкой окружности, катящейся по другой окружности.
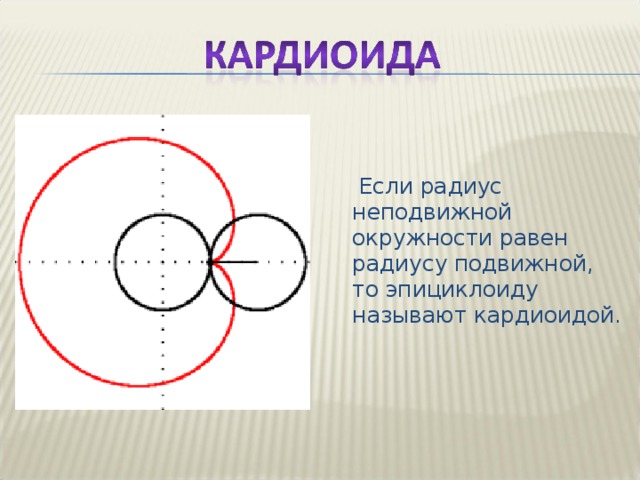
Если радиус неподвижной окружности равен радиусу подвижной, то эпициклоиду называют кардиоидой.
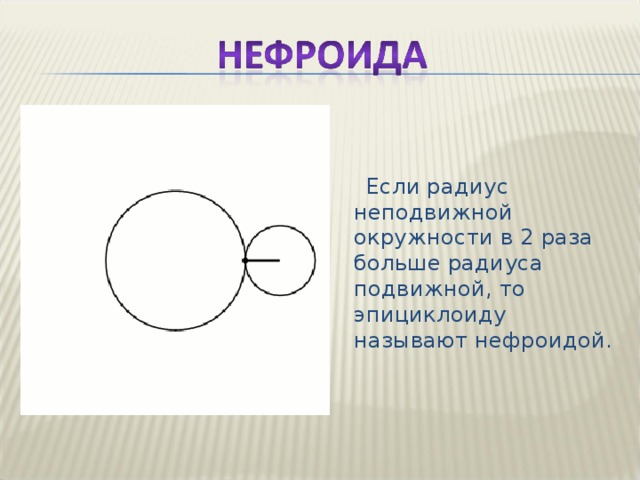
Если радиус неподвижной окружности в 2 раза больше радиуса подвижной, то эпициклоиду называют нефроидой.

- плоская кривая, образуемая точкой окружности, катящейся по внутренней стороне другой окружности без скольжения.
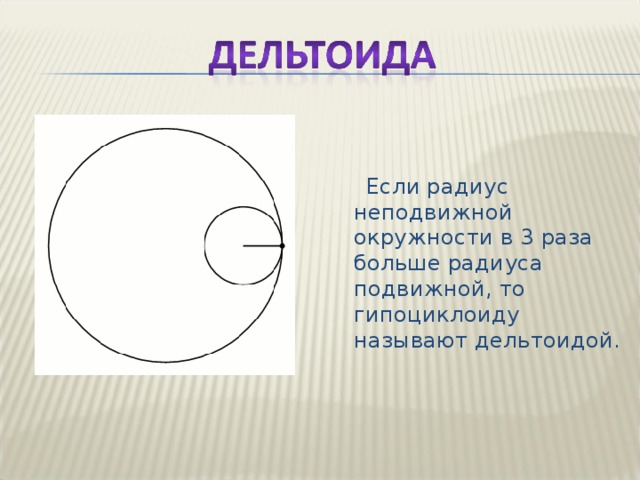
Если радиус неподвижной окружности в 3 раза больше радиуса подвижной, то гипоциклоиду называют дельтоидой.
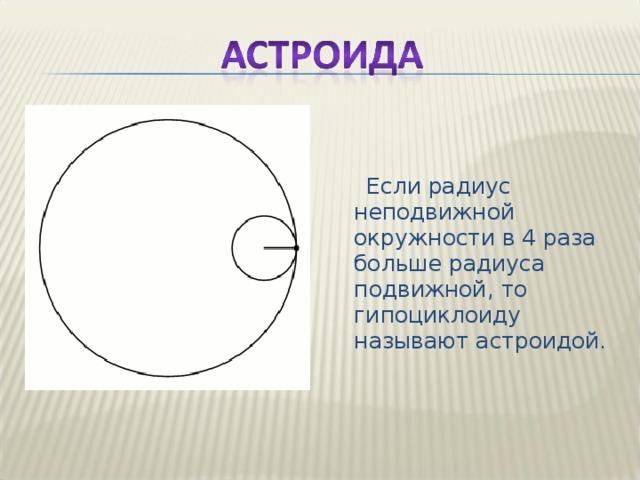
Если радиус неподвижной окружности в 4 раза больше радиуса подвижной, то гипоциклоиду называют астроидой.

Доклад для защиты научно-исследовательского проекта по теме "Циклоида", включающий демонстрацию презентации и опытов на самостоятельно собранной моделе.
Тема моей работы - циклоида.
Цель моего исследования – изучить циклоиду и ее свойства.
Я перед собой поставила следующие задачи:
- Изучить и проанализировать литературу, собрать данные о циклоиде.
- Дать определение циклоиды и показать способы ее построения.
- Изучить биографии ученых, которые занимались циклоидой.
- Изучить свойства, которыми обладает циклоида.
- Провести эксперименты, демонстрирующие свойства циклоиды, имеющие практическое применение.
Осенью я побывала в музее занимательных наук Эйнштейна в Ярославле. Там я узнала об одной замечательной кривой, которая обладает интересными свойствами.
Меня очень заинтересовала эта кривая, и я решила выяснить, какими замечательными свойствами она обладает. Что же такое циклоида?
Одним из древнейших способов образования кривых является кинематический метод.
Кривая, которая получается как траектория движения точки, закрепленной на окружности, катящейся без скольжения по прямой, называется циклоидой.
В 17 веке циклоида стала очень популярной кривой. Ее изучали такие знаменитые ученые, как Декарт, Ньютон, Гюйгенс, Лейбниц и другие. Их жизнедеятельность я изучаю в своей работе.
В процессе исследования я осуществляю построение циклоиды. На слайде Вы можете видеть часть циклоиды, которая называется арка циклоиды. Очевидно, что циклоида бесконечная кривая, состоящая из таких арок.
Ну а сейчас я расскажу о двух замечательных свойствах, которыми обладает циклоида.
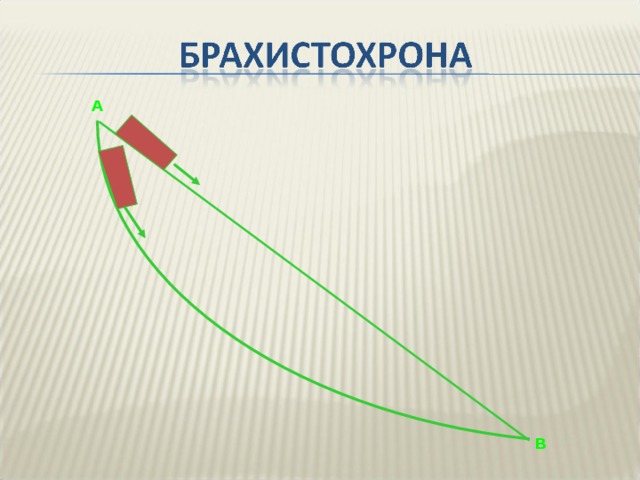
Первое свойство – брахистохронность. Это слово происходит от двух греческих слов: брахисто – кратчайший и хроно – время. То есть речь идет о кривой наискорейшего спуска.
В 1696 году Иоганн Бернулли поставил перед математиками всего мира задачу: найти кривую, по которой должно двигаться тело под действием силы тяжести, чтобы из точки А попасть в точку В за самое короткое время. Искомой кривой оказалось циклоида!
На слайде вы видите 3 горки, изготовленные в форме части окружности, циклоиды и прямолинейную. По какой горке санки скатятся быстрее? По кривой наискорейшего спуска, то есть по циклоиде.
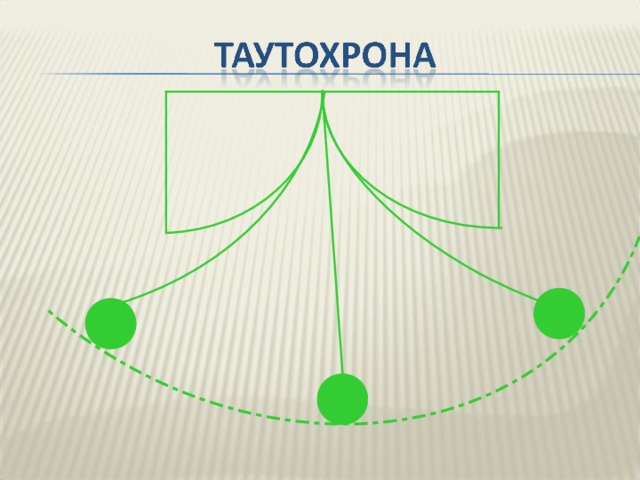
В 1659 году Христиан Гюйгенс обнаружил таутохронное свойство циклоиды. Тауто означает постоянно, а хроно – время. То есть речь идет о равновременной кривой.
На этом слайде Вы можете видеть три горки, изготовленные в форме циклоиды. Если рассмотреть движение санок с разной высоты, то окажется, что санки прибудут на финиш одновременно! То есть время скатывания тела по циклоиде не зависит от точки запуска.
В своем исследовании я экспериментально подтвердила эти свойства, нашла длину арки циклоиды, изготовила макет таутохронного маятника, рассмотрела практическое применение циклоиды.
В результате своего исследования я сделала следующие выводы:
- Циклоида является действительно уникальной кривой!
- Я выяснила, что сейчас циклоида имеет огромное практическое применение, например в перспективных ё мобилях.
- Циклоида неразрывно связана с одним из самых интересных периодов в истории
математики, когда знаменитые ученые изобрели приемы, без которых не может
обойтись современная математика, физика и промышленность.
В продолжение моего исследования мне было бы интересно рассмотреть и другие замечательные кривые, которыми занимались ученые 17 века – спираль Архимеда, улитка Паскаля, кривая Коха и другие.
А сейчас с помощью этого макета я продемонстрирую брахистохронное и таутохронное свойство циклоиды.
Для этого я сделала две горки: одна в форме циклоиды, вторая прямолинейная.
- Запустим одновременно шарик с двух горок. Посмотрим, какой шарик приедет к финишу первым. Первым приехал шарик, который катился по циклоиде. Мы экспериментально доказали брахистохронное свойство циклоиды.
- А теперь отпустим два шарика с разных мест горки в форме циклоиды. Столкновение на финише неизбежно. Так мы доказали таутохронность циклоиды.
Читайте также:

