Что такое случайная функция и случайный процесс реферат

Обновлено: 03.07.2024

69.1. Случайной функцией называется случайная величина , зависимая от параметра . Случайные величины могут быть вещественными, либо комплексными, либо векторными; аргумент может быть вещественным или векторным. Самый простой пример случайной функции получаем для вещественного параметра и вещественной случайной величины . При этом называется случайной функцией одной переменной или случайным процессом. Отметим, что аргумент случайного процесса не обязательно имеет размерность времени.

Более сложные примеры случайных функций встречаются в задачах физики, океанологии, метеорологии и других областях приложения теории вероятностей. Так, температура воздуха в точке пространства и в момент времени часто рассматривается как случайная величина. Таким образом, температура воздуха является случайной функцией, зависимой от трех декартовых координат времени . Случайную функцию, зависимую от нескольких переменных принято называть случайным полем.

69.2. Случайный процесс как функция аргумента имеет свою область определения , которая может быть отрезком на вещественной оси, положительной полуосью, всей вещественной осью и т. д. Рассмотрим случайный процесс при фиксированном , тогда - случайная величина, которая называется сечением случайного процесса в точке .

Пусть выполняется опытов, в каждом из которых измеряется значение , , случайной величины . Тогда результаты измерений - это чисел

В отличие от случайной величины измерение случайного процесса выполняется в течение некоторого интервала -интервала наблюдения. Последний либо содержится в области определения , либо совпадает с ней. Пусть детерминированная функция , , - результат измерения случайного процесса в первом опыте, функция , , - результат измерения случайного процесса во втором опыте, и т.д. Тогда результаты всех опытов, аналогично (69.1), представляются совокупностью детерминированных функций времени:

Каждая функция , , называется реализацией (траекторией, выборочной функцией, выборкой) случайного процесса . Совокупность (69.2) называется ансамблем реализаций случайного процесса . Ансамбль реализаций содержит информацию о статистических свойствах случайного процесса аналогично как и совокупность измерений (69.1) содержит информацию о статистических свойствах случайной величины .

69.3. В зависимости от того, дискретны или непрерывны время и реализации , различают четыре типа случайных процессов.

1). Случайный процесс общего типа: время - непрерывно и реализации - непрерывны.

2). Дискретный случайный процесс: время - непрерывно и - дискретны.

3). Случайная последовательность: - дискретно и - непрерывны. В литературе случайные процессы этого типа принято называть временными рядами.

4). Дискретная случайная последовательность: - дискретно и - дискретны.

Случайный процесс Х(t) представляет собой функцию, которая отличается тем, что ее значения в любые произвольные моменты времени по координате t являются случайными. Строго с теоретических позиций, случайный процесс X(t) следует рассматривать как совокупность множества реализаций функций x_k(t), имеющих общую статистическую закономерность. При регистрации случайного процесса на определенном временном интервале осуществляется фиксирование единичной реализации x_k(t) из бесчисленного числа возможных реализаций процесса X(t). Эта единичная реализация называется выборочной функцией случайного процесса X(t). Примеры выборочных функций модельного случайного процесса X(t) приведены на рис. 131. В дальнейшем без дополнительных пояснений при рассмотрении различных параметров и характеристик случайных процессов для сопровождающих примеров будем использовать данную модель процесса.

Рис. 13.1. Выборочные функции случайного процесса.

С практической точки зрения выборочная функция является результатом отдельного эксперимента, после которого данную реализацию x_k(t) можно считать детерминированной функцией. Сам случайный процесс в целом должен анализироваться с позиции бесконечной совокупности таких реализаций, образующих статистический ансамбль. В каждый выбранный момент времени t₁ конкретная реализация процесса представляет собой случайную величину х₁ с определенной плотностью вероятности p(x₁, t₁), а ее среднее значение определяется усреднением по всем возможным реализациям в этот момент времени t₁. Полной статистической характеристикой такой системы является N-мерная плотность вероятностей р(x_n; t_n). Однако, как экспериментальное определение N-мерных плотностей вероятностей процессов, так и их использование в математическом анализе представляет значительные математические трудности. Поэтому на практике обычно ограничиваются одно- и двумерной плотностью вероятностей процессов.

Рис. 13.2. Сечения случайного процесса X(t).

Функциональные характеристики случайных сигналов . Допустим, что случайный процесс X(t) задан ансамблем реализаций 1(t), x₂(t), … , x_k(t), …>. В произвольный момент времени t₁ зафиксируем значения всех реализаций 1(t₁), x₂(t₁), … , x_k(t₁), …>. Совокупность этих значений представляет собой случайную величину X(t₁) и является одномерным сечением случайного процесса X(t). Примеры сечений по 100 выборкам случайного процесса X(t) (рис. 9.1.1) в точках t₁=30 и t₂=65 приведены на рис. 13.2.

Одномерная функция распределения вероятностей (x, t_n) определяет вероятность того, что в момент времени t_n значение случайной величины X(t_n) не превысит значения x:

Очевидно, что в диапазоне значений вероятностей от 0 до 1 функция F(x, t) является неубывающей с предельными значениями F(-¥, t) = 0 и F(¥, t) = 1. При известной функции F(x, t) вероятность того, что значение X(t_n) в выборках будет попадать в определенный интервал значений [a, b] будет определяться выражением:

Pº = x 2 p(x; t) dx.

Функция дисперсии (variance) – второго центрального момента случайного процесса, определяет функцию среднего взвешенного значения (математического ожидания) квадрата разности Х(t)-m_x(t), которая называется флюктуационной частью процесса:

Функция среднего квадратического отклонения (standard deviation) служит амплитудной мерой разброса (флюктуаций) значений случайного процесса по временной оси относительно математического ожидания процесса:

Учитывая последнее выражение, дисперсия случайной величины обычно обозначается индексом s_x 2 .

На рис. 13.4 приведен пример флюктуационной составляющей процесса X(t) (рис. 13.1) в одной из реализаций в сопоставлении со средним квадратическим отклонением ±s случайных величин от математического ожидания m(t).

Вид функций плотности вероятностей в сечениях случайных процессов p(x; t_n), а также по всем сечениям стационарных случайных процессов р(х), зависит от физической природы случайных сигналов , но чаще всего соответствует нормальному (гауссову) распределению:

Это определяется тем, что в соответствии с "центральной предельной теоремой" распределение вероятностей для сумм независимых случайных величин, при которых нет доминирующих, стремится к нормальному закону по мере роста числа слагаемых, и не зависит от законов распределения слагаемых. Между тем физические случайные процессы обычно являются многопараметровыми, при этом случайность значений параметров, как правило, обусловлена их природой и также соответствует нормальным распределениям.

Двумерная плотность вероятностей. Одномерные законы плотности распределения вероятностей случайных процессов не несут каких-либо характеристик связи между значениями случайных величин для различных значений аргументов.

Двумерная плотность вероятностей p(x₁,x₂; t₁,t₂) определяет вероятность совместной реализации значений случайных величин Х(t₁) и Х(t₂) в произвольные моменты времени t₁ и t₂ и в какой-то мере уже позволяет оценивать динамику развития процесса. Двумерная плотность вероятностей описывает двумерную случайную величину n), X(t_m)> в виде функции вероятности реализации случайной величины X(t_n) в бесконечно малом интервале dx_n в окрестностях x_n в момент времени t_n при условии, что в момент времени t_m значение X(t_m) будет реализовано в бесконечно малом интервале dx_m в окрестностях x_m:

При двумерной плотности вероятности имеем:

Корреляционные функции случайных процессов. Характеристикой динамики изменения двумерной случайной величины n), X(t_m)> является корреляционная функция, которая описывает случайный процесс в целом:

Корреляционная функция представляет собой статистически усредненное произведение значений случайного процесса X(t) в моменты времени t_n и t_m по всем значениям аргументов t_n и t_m, а, следовательно, тоже является двумерной функцией. В терминах теории вероятностей корреляционная функция является вторым начальным моментом случайного процесса.

На рис. 13.5 приведены примеры реализаций двух случайных процессов, которые характеризуются одной и той же функцией математического ожидания и дисперсии.

На рисунке видно, что хотя пространство состояний обоих процессов практически одно и то же, динамика развития процессов в реализациях существенно различается. Единичные реализации коррелированных процессов в произвольный момент времени могут быть такими же случайными, как и некоррелированных, а в пределе, во всех сечениях оба процесса могут иметь один и тот же закон распределения случайных величин. Однако динамика развития по координате t (или любой другой независимой переменной) единичной реализации коррелированного процесса по сравнению с некоррелированным является более плавной, а, следовательно, в коррелированном процессе имеется определенная связь между последовательными значениями случайных величин. Оценка степени статистической зависимости мгновенных значений какого-либо процесса Х(t) в произвольные моменты времени t_n и t_m и производится функцией корреляции. По всему пространству значений случайного процесса X(t) корреляционная функция определяется выражением:

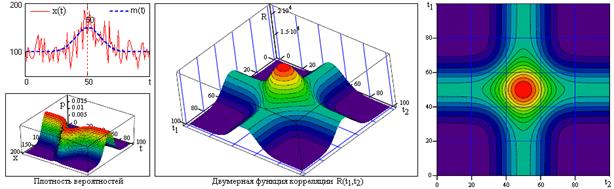
Рис. 13.6. Двумерная плотность вероятностей и корреляционная функция процесса X(t).

На рис. 13.6 приведена форма модельного случайного процесса X(t) в одной выборке со значительной и изменяющейся неслучайной составляющей. Модель задана на интервале 0-Т (Т=100) в дискретной форме с шагом Dt=1. Корреляционная функция вычислена по заданной плотности вероятностей модели.

При анализе случайных процессов второй момент времени t_m удобно задавать величиной сдвига t относительно первого момента, который при этом может быть задан в виде координатной переменной:

Функция, задаваемая этим выражением, обычно называется функцией автокорреляции случайного процесса.

Ковариационные функции. Частным случаем корреляционной функции является функция автоковариации (ФАК), которая широко используется при анализе сигналов. Она представляет собой статистически усредненное произведение значений центрированной случайной функции X(t)-m_x(t) в моменты времени t_n и t_m и характеризует флюктуационную составляющую процесса:

В терминах теории вероятностей ковариационная функция является вторым центральным моментом случайного процесса. Для центрированных случайных процессов ФАК тождественна функции корреляции. При произвольных значениях m_x ковариационные и корреляционные функции связаны соотношением:

Нормированная функция автоковариации (функция корреляционных коэффициентов):

При t= 0 значение r_Х равно 1, а ФАК вырождается в дисперсию случайного процесса:

Отсюда следует, что для случайных процессов и функций основными характеристиками являются функции математического ожидания и корреляции (ковариации). Особой необходимости в отдельной функции дисперсии не имеется.

Примеры реализаций двух различных случайных процессов и их нормированных ковариационных функций приведены на рис. 13.7.

Ансамбль функций времени является случайным процессом.

Случайными процессами называются такие процессы, которые математически описываются случайными функциями времени. Случайной называется функция, значения которой при каждом значении аргумента являются случайными величинами.

Случайная функция времени , описывающая случайный процесс, в результате опыта принимает ту или иную конкретную форму , неизвестную заранее. Эти возможные формы случайной функции называются реализациями случайного процесса.

Мгновенные значения случайного процесса в фиксированный момент времени t_i являются случайными величинами и называются сечением случайного процесса.

Статистические свойства случайного процесса как множества (ансамбля) реализации , характеризуются законами распределения, аналитическими выражениями которых являются функции распределения.

Для некоторого фиксированного момента времени t_i одномерная функция распределения

определяет вероятность того, что мгновенное значение случайного процесса в этот момент времени примет значение, меньшее или равное X, то есть вероятность того, что .

В общем случае скалярный процесс X(t) полностью задан, если для любого набора моментов времени и любых значений можно вычислить вероятность того, что X(t) принимает в указанные моменты времени значения, не превышающие соответственно .

Функция называется n-мерной функцией распределения вероятности процесса.

Если существует частная производная функции распределения по x_i , то можно определить плотность распределения вероятности. Одномерная плотность распределения вероятностей случайного процесса определяется соотношением

Аналогично определяются многомерные (n-мерные) функции распределения для совокупности моментов времени t₁ , t₂ . t_i . t_n , которые более полно характеризуют случайный процесс одновременно в n сечениях, обозначаемые как

В теории связи наиболее широкое применение находят двумерные функции распределения

Во многих практических случаях для характеристики случайных процессов достаточно знать лишь его усредненные, так называемые, числовые характеристики (моментные функции). Наиболее часто используются математическое ожидание (первый начальный момент), дисперсия (второй центральный момент), ковариационная функция и корреляционная функция.

Простейшей характеристикой случайного процесса является его математическое ожидание

которое представляет собой неслучайную функцию времени, около которой различным образом располагаются отдельные реализации случайного процесса.

Математическое ожидание случайного процесса - сигналов электросвязи представляет собой постоянную составляющую.

Дисперсией случайного процесса называется неслучайная функция времени, значения которой для каждого момента времени равны математическому ожиданию квадрата отклонения случайного процесса от его математического ожидания

Дисперсия определяет степень разброса значений случайного процесса около математического ожидания.

Применительно к сигналам электросвязи дисперсия является мощностью переменной составляющей на нагрузке 1 Ом и измеряется в Ваттах.

Случа́йный проце́сс (случайная функция) в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или пространства.

Содержание

Определение

Пусть дано вероятностное пространство ,\mathbb)" width="" height="" />
. Параметризованное семейство _" width="" height="" />
случайных величин

$X_t(\cdot) : \Omega \to \mathbb<R></p> <p>,\quad t \in T$
,

где T произвольное множество, называется случайной функцией.

Терминология

Данная классификация нестрогая. В частности термин случайный процесс часто используется как безусловный синоним термина случайная функция.

Классификация

$\;t_1, t_2, \ldots, t_n$

Случайный процесс называется стационарным, если все многомерные законы распределения зависят только от взаимного расположения моментов времени , но не от самих значений этих величин. В противном случае, он называется нестационарным.
Случайная функция называется стационарной в широком смысле, если её математическое ожидание и дисперсия постоянны, а АКФ зависит только от разности моментов времени, для которых взяты ординаты случайной функции. Понятие ввёл А. Я. Хинчин.
Если ординаты случайной функции подчиняются нормальному закону распределения, то и сама функция называется нормальной.
Случайные функции, закон распределения ординат которых в будущий момент времени полностью определяется значением ординаты процесса в настоящий момент времени и не зависит от значений ординат процесса в предыдующие моменты времени, называются марковскими.
Случайный процесс называется процессом с независимыми приращениями, если

Если при определении моментных функций стационарного случайного процесса операцию усреднения по статистическому ансамблю можно заменить усреднением по времени, то такой стационарный случайный процесс называется эргодическим.

Замечание

Пусть дан случайный процесс _" width="" height="" />
. Тогда для каждого фиксированного X_t — случайная величина. Если фиксирован элементарный исход , то " width="" height="" />
— детерминистическая функция параметра t . Такая функция называется траекто́рией или реализа́цией случайной функции X_t> .

Читайте также: