Частотные характеристики сау реферат
Обновлено: 05.07.2024
Свойства звена или системы при изменении во времени входных и выходных величин определяют динамические характеристики. Динамические характеристики делятся на два вида: временные и частотные.
Временной анализ. Для анализа динамических свойств во временной области служат переходная и импульсная переходная функции.
Переходной функцией h(t) называют реакцию звена или системы на единичное ступенчатое воздействие u(t)=1(t) на входе, при нулевых начальных условиях. Выражение связывающее h(t) и W(s) имеет вид
Графическое изображение переходной функции называется переходным процессом h(t). Вид h(t) определяется внутренними свойствами САУ. Система с расходящимся переходным процессом будет неустойчивой и неработоспособной.
Для устойчивой САУ переходный процесс имеет сходящийся вид (рис. 10 а) . Для неустойчивой – расходящийся (рис. 10 б).
Рис. 10. Виды переходных процессов:
a – сходящиеся для устойчивых, б – расходящиеся для неустойчивых систем
Импульсной переходной функцией k(t) звена или системы называют реакцию на единичное импульсное воздействие u(t)=δ(t) при нулевых начальных условиях.
Характеристика k(t) является производной от h(t) и представляет собой оригинал передаточной функции
Частотный анализ. Традиционной формой [1–4] представления линейных моделей, удобной для проведения анализа динамических свойств исследуемой системы, является частотная форма. Описание в частотной области определяется набором частотных функций и частотных характеристик, как их графического отображения.
К частотным характеристикам относятся:
– частотная передаточная функция или комплексный коэффициент усиления ;
– вещественная частотная характеристика =ReW(jω);
– мнимая частотная характеристика Q(ω);
– амплитудная частотная характеристика A(ω);
– фазовая частотная характеристика .
Частотная передаточная функция может быть представлена в двух формах алгебраической и показательной:
Формулы взаимных пересчетов этих двух форм очевидны и имеют вид:
Частотная форма удобна для проведения анализа динамических свойств исследуемой системы.
Графические представления частотных и временных функций принято называть характеристиками. В табл. 2 приведены наименования типовых частотных и временных характеристик САУ.
К типовым задачам частотного и временного анализа моделей САУ с одним входом и одним выходом относятся:
– расчет общей передаточной функции по передаточным функциям отдельных звеньев структурной схемы;
Типовые характеристики САУ
| Обозначение функции | Наименование характеристики | Сокращенное наименование |
| W(ω) | Амплитудно-фазовый годограф | АФГ |
| A(ω) | Амплитудная частотная характеристика | АЧХ |
| L(ω)=20lgA(ω) | Логарифмическая амплитудная частотная характеристика | ЛАЧХ |
| φ(ω) | Фазовая частотная характеристика | ФЧХ |
| P(ω) | Вещественная частотная характеристика | ВЧХ |
| Q(ω) | Мнимая частотная характеристика | МЧХ |
| h(t) | Переходная характеристика | |
| k(t) | Импульсная переходная характеристика |
– расчет постоянных времени, коэффициентов затухания и статического коэффициента усиления модели;
– разложение полиномов числителя и знаменателя передаточной функции системы на элементарные сомножители;
– нахождение корней характеристического уравнения;
– построение частотных характеристик: ЛАЧХ, ЛФЧХ, АФГ;
– построение временных переходных характеристик: h(t) и k(t).
Контрольные вопросы.
1. Как определяется устойчивость по расположению полюсов?
2. Можно ли судить об устойчивости объекта управления по коэффициентам характеристического полинома?
3. Какие критерии устойчивости вам известны?
4. Раскройте физический смысл понятия устойчивость.
5. Какие виды частотного и временного анализа вы знаете?
6. Что такое переходный процесс?
7. Как по виду переходного процесса оценить устойчивость САУ?
8. Как по передаточной функции можно определить величину, к которой будет стремиться переходный процесс?
Лабораторная работа 1
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.



Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Статические характеристики определяют статику системы, т.е. ее поведение в установившемся режиме.
Статической характеристикой называется отношение выходной величины к входной величине в установившемся режиме.
Статические характеристики позволяют: определить коэффициент усиления системы; степень ее нелинейности; величину статизма; произвести согласование рабочих точек системы.
Динамические характеристики определяют динамику системы, т.е. ее поведение в неустановившемся (переходном) режиме. При этом используют следующие основные динамические характеристики:
– передаточная функция;
– временные характеристики;
– частотные характеристики.
Дифференциальное уравнение линейной системы имеет вид:

(1)
где аi и bi – параметры системы, n -порядок системы.
Если применим теоремы Лапласа при нулевых начальных условиях, то дифференциальное уравнение в операторной форме запишется следующим образом


где
Физически нулевые начальные условия обозначают, что до приложения воздействия система находилась в покое.
Передаточная функция системы есть отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях

(2)
Основные свойства передаточной функции:
1. Передаточная функция является полной характеристикой системы.
Она полностью характеризует статические и динамические свойства системы.
2. Статический коэффициент усиления, т.е. коэффициент усиления в установившемся режиме (при t ® ¥ или p ® 0) равен

.
3. Полином знаменателя называется характеристическим, а A(p) = 0 называется характеристическим уравнением. Корни полинома знаменателя называются полюсами, а числителя нулями.
Степень полинома числителя не превышает степени полинома знаменателя (n ³ m ), в противном случае система является физически нереализуемой.
5. Коэффициенты полиномов ai и bi обусловлены реальными физическими параметрами системы.
6. Передаточная функция может быть задана в виде нулей и полюсов в графическом виде.

Например, для приведенного на рис. 1 расположения нулей (0) и полюсов (х) передаточная функция имеет вид:

.
2.2 Временные характеристики САУ
Временной характеристикой системы называется закон изменения выходной величины в функции времени при изменении входного воздействия по определенному закону и при условии, что до приложения воздействия система находилась в покое. Временные характеристики определяются как реакция системы на типовые воздействия при нулевых начальных условиях.
К основным временным характеристикам относятся переходная функция и функция веса.
Типовые воздействия . В качестве типовых воздействий при исследовании систем используются:
– единичная функция;
– единичный импульс;
– линейно – растущее воздействие;
– квадратичное воздействие;
– гармоническое воздействие;
Виды типовых задающих воздействий. Показатели, характерные для апериодического переходного процесса, возникающего в системе. Типовые функции входного сигнала. Линейная система автоматического управления под воздействием гармонического возмущения.
| Рубрика | Коммуникации, связь, цифровые приборы и радиоэлектроника |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 29.01.2011 |
| Размер файла | 58,3 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Временные и частотные характеристики систем автоматического управления (САУ) - 4 часа
1. Виды типовых задающих воздействий
Для оценки динамических свойств системы необходимо решить дифференциальное уравнение системы, что возможно только при заданном задающем воздействии. Однако в реальных условиях работы задающее воздействие может быть любой функцией времени. Более того, она может менять свой характер при переходе от одного режима работы системы к другому. Чтобы не решать каждый раз частную задачу исследования динамики элемента при конкретном входном сигнале, а получить довольно полное представление о динамических свойствах элемента в результате одного решения уравнения динамики, целесообразно ввести некоторое типовое задающее воздействие, которое отражает наиболее вероятный режим работы элементов.
В качестве типовых задающих воздействий используют:
Рисунок 1 Типовые функции входного сигнала
1) единичное ступенчатое воздействие 1(t) - это функция, неизменная по величине и равная единице для всех моментов времени t>0, а при всех значениях t iц ( w )
- частота входного сигнала.
На комплексной плоскости частотная передаточная функция W(jw) определяет вектор ОС, длина (модуль) которого равна A(w), а угол, образованный этим вектором с действительной положительной полуосью, равен (w). Кривая, которую описывает конец этого вектора при изменении частоты от 0 до бесконечности (годограф вектора W(jw)), называется амплитудно-фазовой частотной характеристикой (АФЧХ).
2. АФЧХ - это кривая, которую описывает конец вектора ОС при изменении частоты от 0 до бесконечности, т.е. годограф вектора.
Годограф вектора W(jw) - геометрическое место концов векторов, соответствующих передаточной функции W(jw) при изменении частоты от 0 до бесконечности.
Для определения модуля и фазы комплексного, коэффициента усиления на заданной частоте следует соответствующую точку годографа соединить прямой с началом координат. Длина полученного, отрезка соответствует в определенном масштабе модулю, а фаза определяется углом, образованным этой прямой и положительной полуосью действительных величин.
3. Вещественна частотная функция
U(w) = Re W (jw)
U(w) = A(w) cos (w)
График зависимости U от w наз вещественной частотной характеристикой.
4. Мнимая частотная функция
V(w) = Im W (jw)
V(w) = A(w) sin (w)
График зависимости V от w называют вещественной частотной характеристикой.
5. Амплитудно-частотная функция (АЧФ) - определяется отношением амплитуды выходного сигнала к амплитуде входного гармонического сигнала в установившемся режиме: А=b/a.
АЧФ определяется как модуль частотной передаточной функции:
A(w) = |W (jw)| =
График зависимости А от w называют амплитудно-частотной характеристикой (АЧХ). Она показывает как пропускает звено сигнал различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин.
6. Фазо-частотная функция (ФЧФ) - определяется сдвигом фазы выходного сигнала (w)=
ФЧФ определяется как аргумент частотной передаточной функции:
(w) = argW (jw) = arctg V(w)/U(w)
График зависимости от w называют фазо-частотной характеристикой (ФЧХ). Она показывает фазовые сдвиги вносимые звеном на различных частотах Оценка пропускания делается по отношению амплитуд выходной и входной величин.
При расчетах систем пользуются логарифмической амплитудно-частотной (ЛАЧХ) и логарифмической фазочастотной (ЛФЧХ) характеристиками. В этом случае по горизонтальной оси откладывают частоту в логарифмическом масштабе, что позволяет отложить на заданном отрезке значительный диапазон частот. Эта наиболее удобная форма представления частотных характеристик для решения задач анализа и синтеза систем.
Рассмотрим координатную систему для такого представления (рис 6.). По оси абсцисс откладываем величину lg w. Вводим единицу измерения: декаду. Декада - длина отрезка по оси абсцисс, соответствующая десятикратному изменению частоты.
Октава - длина отрезка по оси абсцисс, соответствующая двухкратному изменению частоты. В одной декаде содержится 3,32 октавы. Декадный интервал применяют чаще.
Рисунок 6. - Координатная система для построения ЛАЧХ и ЛФЧХ
Фазу обычно откладывают по оси ординат в угловых градусах или в радианах. Ординатой амплитудно-частотной характеристики является величина lg K(w), а пропорциональная ей величина L(w) в децибелах, L(w) = 20 lg K(w) (шкала равномерная). Точка пересечения с осью абсцисс соответствует K(w)=1.
Использование логарифмического масштаба при построении ЛАЧХ обусловлено не столько значительными изменениями модуля комплексного коэффициента усиления, сколько возможностью осуществления графических методов расчета. При расчетах САУ часто приходится иметь дело с произведением коэффициентов усиления. А так как логарифм произведения равен сумме логарифмов, то при графических расчетах для получения произведения нескольких значений весьма удобно осуществить сложение их логарифмов. Удобство логарифмического масштаба по оси ординат в том, что на одном графике можно представить значения, отличающиеся на несколько порядков.
Подобные документы
Общие принципы построения систем автоматического управления, основные показатели их качества. Передаточная функция разомкнутой и замкнутой систем. Определение устойчивости системы. Оценка точности отработки заданных входных и возмущающих воздействий.
реферат [906,1 K], добавлен 10.01.2016
Системы управления нитью накала, принцип их действия, структура, конструкции и элементы. Технические характеристики фоторезистора. Расчет передаточной функции. Определение амплитуды входного сигнала и колебательности системы автоматического регулирования.
курсовая работа [1,2 M], добавлен 20.10.2013
Состав частотных и логарифмических частотных характеристик. Частотные характеристики апериодического, интегрирующего, колебательного и идеального дифференцирующего звеньев. Уравнение динамических свойств колебательного и апериодического звеньев.
контрольная работа [16,2 K], добавлен 06.10.2015
Системы автоматического регулирования (САР), их виды и элементарные звенья. Алгебраические и графические критерии устойчивости систем. Частотные характеристики динамических звеньев и САР. Оценка качества регулирования, коррекция автоматических систем.
курсовая работа [1,5 M], добавлен 16.02.2013
Описание объекта автоматического управления в переменных состояниях. Определение дискретной передаточной функции замкнутой линеаризованной аналого-цифровой системы. Графики переходной характеристики, сигнала управления и частотных характеристик системы.
курсовая работа [1,7 M], добавлен 21.11.2012
Расчет передаточной функции разомкнутой и замкнутой цепи. Построение переходного процесса системы при подаче на вход сигнала в виде единичной ступеньки. Исследование устойчивости системы по критерию Гурвица и Михайлова. Выводы о работоспособности системы.
контрольная работа [194,0 K], добавлен 19.05.2012
Параметры регулируемой системы, передаточная и амплитудно-частотная функция, график переходного процесса. Построение логарифмической характеристики системы автоматического управления. Синтез параллельного корректирующего звена и программного устройства.
Частотные характеристики САУ характеризуют реакцию систем на синусоидальное входное воздействие в установившемся режиме.
К частотным характеристикам относятся:
АФЧХ - амплитудно-фазовая частотная характеристика;
АЧХ - амплитудно-частотная характеристика;
ФЧХ - фазовая частотная характеристика;
ЛАЧХ - логарифмическая АЧХ;
ЛФЧХ - логарифмическая ФЧХ.
АФЧХ представляет собой частотную передаточную функцию W(jω), которая получается путем замены в передаточной функции W(p) оператора Лапласа p на комплексную переменную jω. АФЧХ представляет собой вектор на комплексной плоскости в полярных координатах Н(ω) и φ(ω), которые являются соответственно АЧХ и ФЧХ:
W(jω) = Н(ω)∙е jφ ( ω ) = N(ω) + jM(ω). (1)
Здесь: Н(ω) - АЧХ, которая представляет собой зависимость значения модуля вектора АФЧХ от круговой частоты;
φ(ω) - ФЧХ, которая представляет собой зависимость аргумента вектора АФЧХ от круговой частоты;
N(ω) = Н(ω)∙cosφ(ω) - проекция вектора АФЧХ на действительную ось комплексной плоскости;
M(ω) = Н(ω)∙sinφ(ω) - проекция вектора АФЧХ на мнимую ось комплексной плоскости;
При изменении частоты ω от нуля до бесконечности АФЧХ представляет собой кривую в комплексной плоскости, называемую годографом.
Рассмотрим частотные характеристики отдельных типовых звеньев.
Апериодическое звено.
Основные формулы и соотношения
Н(ω) = ; φ(ω) = - arctg(ωT);
N(ω) = K/[1 + (ω∙T) 2 ]; M(ω) = - K∙ ω∙T/[1 + (ω∙T) 2 ]. (2)
φ(0) = 0 o ; Н(0) = K; N(0) = K; M(0) = 0;
φ(ω = 1/T) = - 45 o ; Н(T) = K/√2; N(T) = K/2; M(T) = - K/2;
φ(ω → ∞) = - 90 o ; Н(∞) = N(∞) = M(∞) = 0.
Интегрирующее звено.

Основные формулы и соотношения
Н(ω) = K/ω; φ(ω) = - 90 o ;(ω) = 0; M(ω) = - K/ω; (3)
φ(0) = - 90 o ; Н(0) = ∞; N(0) = 0; M(0) = - ∞;
φ(ω → ∞) = - 90 o ; Н(∞) = N(∞) = M(∞) = 0.
Колебательное звено.
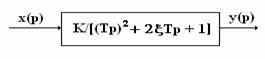
Основные формулы и соотношения
W(jω) = K/[- (ω∙T) 2 + j2ξ∙T∙ω + 1] = =
φ(0) = 0 o ; Н(0) = K; N(0) = K; M(0) = 0;
φ(ω = 1/T) = - 90 o ; Н(T) = K/(2ξ); N(T) = 0; M(T) = - K/(2ξ);
φ(ω → ∞) = - 180 o ; Н(∞) = N(∞) = M(∞) = 0.
Идеальное дифференцирующее звено.

Основные формулы и соотношения
Н(ω) = K∙ω; φ(ω) = 90 o ;(ω) = 0; M(ω) = K∙ω; (5)
φ(0) = 90 o ; Н(0) = 0; N(0) = 0; M(0) = 0;
φ(ω → ∞) = 90 o ; Н(∞) = M(∞) = ∞; N(∞) = 0.
Кроме перечисленных ранее частотных характеристик при анализе свойств САУ широко используются логарифмические частотные характеристики, к которым относятся:
ЛАЧХ - логарифмическая амплитудно-частотная характеристика;
ЛФЧХ - логарифмическая фазовая частотная характеристика.
ЛАЧХ представляет собой график зависимости L(ω) = 20lg[H(ω)] от десятичного логарифма частоты lg(ω). При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе, а по оси ординат L(ω). Единицей L(ω) является децибел (дБ), равный одной десятой Бела. L(ω) = 20 означает, что на данной частоте при прохождении сигнала через звено его амплитуда увеличивается в 10 раз.
ЛФЧХ - это график зависимости частотной функции φ(ω) от десятичного логарифма частоты lg(ω). При его построении по оси абсцисс откладывают частоту в логарифмическом масштабе, по оси ординат откладывают φ(ω) в градусах или радианах.
В обоих случаях за единицу масштаба по оси абсцисс принимается декада - это частотный интервал, соответствующий изменению частоты в 10 раз. Ось ординат при построении этих характеристик проводят часто через точку (ω = 1) которая соответствует началу координат lg(1) = 0.
На практике часто кривую линию ЛАЧХ заменяют приближенным графиком, состоящим из нескольких пересекающихся прямых отрезков (асимптот), к которым стремится логарифмическая функция при определенных значениях частот, называемых сопрягающими частотами.
Рассмотрим аналитические выражения для ЛАЧХ и правила построения асимптотических ЛАЧХ для ряда характерных типовых звеньев.
Апериодическое звено. Формула ЛАЧХ согласно (2) принимает следующий вид:
L(ω) = 20lg[H(ω)] = 20lgК - 20lg . (6)
В области низких частот ω ωc L(ω) = 20lgК - 20lg(ω∙Т). В этой области частот кривая ЛАЧХ заменяется прямой линией, имеющей наклон минус 20 дБ на декаду.
Обе прямые или иначе асимптоты пересекаются в точке, соответствующей сопрягающей частоте ωc = 1/T.
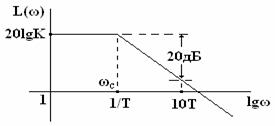
Интегрирующее звено. Формула ЛАЧХ согласно (3) принимает следующий вид:
L(ω) = 20lg[H(ω)] = 20lgК - 20lgω. (7)
Так как при частоте ω = 1 согласно выражению (7) функция L(ω) = 20lgК, то естественно асимптота в виде прямой линии с отрицательным наклоном в 20 дБ должна проходить через эту точку при ω = ωc = 1.
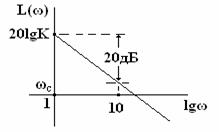
Колебательное звено. Формула ЛАЧХ согласно (4) принимает следующий вид:
L(ω) = 20lg[H(ω)] = 20lgK - 20lg . (8)
В области низких частот ω ωc можно под корнем пренебречь единицей и слагаемым 4(ξ∙ω∙T) 2 . В результате получаем уравнение асимптотической ЛАЧХ:
Согласно уравнению (9) асимптотическая ЛАЧХ при ω r , где r - порядок астатизма. Соответственно, при r = 1 и ω = 0 характеристика W(jω) уходит в бесконечность вдоль отрицательной мнимой полуоси, при r = 2 - вдоль отрицательной действительной полуоси, а при r = 3 - вдоль положительной мнимой полуоси.
Логарифмический критерий Найквиста. Для оценки устойчивости САУ по данному критерию используются графики ЛАЧХ и ЛФЧХ разомкнутой системы САУ. Система САУ считается устойчивой, если при φ(ω) = - 180 о кривая ЛАЧХ находится в отрицательной области: L(ω) = 20lg[H(ω)] о . Систему САУ можно считать также устойчивой, если на частоте среза ωср, на которой L(ωср) = 20lg[H(ωср)] = 0, значение аргумента φ(ωср) > - 180 o .
При оценке устойчивости САУ необходимо определить запас устойчивости, т.е. степень удаленности системы от границы устойчивости. В качестве меры запаса устойчивости используется запас устойчивости по амплитуде h(ω) и запас устойчивости по фазе ψ(ωср).
Запас устойчивости САУ по амплитуде h(ω) определяется на частоте ωу, при которой φ(ωу) = - 180 о : h(ωу) = - L(ωу) и показывает допустимое увеличение ЛАЧХ , при котором система окажется на грани устойчивости. Запас по амплитуде представляет собой запас по коэффициенту усиления К разомкнутой системы по отношению его к критическому по устойчивости значению.
Запас устойчивости по фазе ψ(ωср) определяется на частоте среза ωср, как: ψ(ωср) = φ(ωср) + 180 о и показывает, на какую величину должно возрасти запаздывание по фазе в системе на частоте среза ωср, чтобы система оказалась на грани устойчивости.
При проектировании САУ рекомендуется выбирать ψ(ωср) ≥ 30 о , а h(ωу) ≥ 6 дБ, что соответствует примерно двойному запасу коэффициента усиления К по устойчивости.
Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
В этом разделе мы будем изучать частотные характеристики. Тема сегодняшней статьи:
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ
Будет интересно, познавательно и жестко.

3.1. Амплитудно-фазовая частотная характеристика: годограф АФЧХ, ЛАХ, ФЧХ
Определение: Частотными характеристиками называются формулы и графики, характеризующие реакцию звена (системы) на единичное синусоидальное воздействие в установившемся режиме, т.е. в режиме вынужденных гармонических колебаний звена (системы).

Формула синусоидального воздействия может быть записана как:

— сдвиг фазы (нередко называют — фаза);
— амплитуда;
т.е. амплитуда на выходе звена(системы) и сдвиг фазы зависят от частоты входного воздействия x(t).
Используем показательную форму записи функции единичного гармонического воздействия и отклика на это воздействие (рис. 3.1.1):
Определим связь между передаточной функцией и гармоничным воздействием, пользуясь показательной формой.
Рассмотрим звено уравнение динамики которого имеет следующий вид:
В показательной форме:
Запишем в показательной форме используя соотношения 3.1.1:
Подставим эти соотношения в (3.1.1) получим:
Поскольку (амплитуда на выходе звена(системы) и сдвиг фазы зависят от частоты входного воздействия), то можно записать:
если вспомнить, что в преобразования Лапласа , то:
Получаем выражение для передаточной функции
— Амплитудно-фазовая частотная характеристика (АФЧХ)
Иногда называют частотной передаточной функцией.
Модуль АФЧХ= тождественно равен амплитуде выходного сигнала:
Сдвиг фазы выходного сигнала:
Обычно АФЧХ изображается на комплексной плоскости. Формулы (3.1.6) и (3.1.7) позволяют изобразить в полярных координатах
Так же можно изображать в традиционных декартовых координатах:
Если использовать для представления W(s) форму W(s)=K·N(s)/L(s), где L(s)- полиномы по степеням s, (причем свободные члены равны 1), а К – общий коэффициент усиления звена (системы), то
Сдвиг фазы можно определить по виду многочленов и (см. формулу (3.1.9)) т.е. как разность фаз (аргументов) числителя и знаменателя:
Подставляя в формулу различные значения , получаем набор векторов, на комплексной плоскости

Рассмотрим действительную и мнимую части полученных векторов Из рисунка 3.1.3 видно, что:
Амплитуда и сдвиг фазы рассчитываются для векторов, соответствующих положительным частотам и лежащих в 4 квадранте по формулам:
В общем случае для любых углов сдвига необходимо учитывать переход между квадрантами на плоскости. Тогда формула принимает вид:
где:
j = 0, 2, 3, 4. если вектор в I и IV квадрант;
j = 1, 3, 4, 4. если вектор в II и III квадранте.
Во всех технических системах отклик системы, как правило, отстает от входного воздействия, то есть сдвиг фазы всегда отрицательный. Исходя из формулы 3.1.10, степень полинома L(s) выше, чем полинома N(s). Поскольку обычно степень полинома L(s) выше, чем полинома N(s), то с увеличением частоты на входе в звено (в систему) сдвиг фазы обычно отрицателен, т.е. сигнал на выходе звена еще больше отстает по фазе от входного сигнала при увеличении частоты.
В предельном случае, если частота растет до бесконечности, мы можем вообще не получить выходного воздействия. Обычно при ω→ ∞ величина амплитуды на выходе звена стремится к 0, то есть lim A(ω→∞) = 0.
при замене на имеет зеркальное изображение.

Кроме анализа свойств звена (системы) по годографу АФЧХ, широкое распространение получили анализ логарифмической амплитудной характеристики (ЛАХ) и фазочастотной характеристики (ФЧХ).
ЛАХ определяется как Lm(ω)=20lgA(ω).
Поскольку зачастую удобнее использовать десятичные логарифмы (lg), чем натуральные(ln), в теории управления (также и в акустике) значительно чаще используется специальная единица – децибел (1/10 часть Бела):
+1Бел – единица, характеризующая увеличение в 10 раз.
+1дБ (децибел) – соответствует увеличению в раз.
В формуле Lm(ω)=20lgA(ω) величина Lm(ω) измеряется также в децибелах. Происхождение множителя 20 таково: A(ω) – амплитуда, линейная величина, а мощность — квадратичная величина (например, напряжение в сети измеряется в Вольтах, а мощность () пропорциональна квадрату напряжения, поэтому в формуле для Lm(ω) стоит множитель 20 (чтобы привести ЛАХ (Lm(ω)) к традиционной мощностной характеристике).
Если больше на 20 дБ, то это означает, амплитуда больше амплитуды в 10 раз,
Окончательно: Lm(ω)=20lg│W(iω)│= 20lgA(ω)
Из этого следует, что +1 децибел (+1 дБ) соответствует увеличению амплитуды в раз (очень малая величина); -1 дБ – уменьшение амплитуды в раз.
Графики A(ω) и φ(ω) имеют вид:


Учитывая, что “ω” обычно изменяется на порядки и значение A(ω) – также на порядки, график Lm(ω) строится, фактически, в логарифмических координатах, т.е. Lm(ω) =Lm(lg(ω)), например:

Наклон (– 40 дБ/дек) соответствует уменьшению амплитуды в 100 раз при увеличении частоты в 10 раз.

Рассмотренные характеристики Lm(ω), то есть ЛАХ и ФЧХ имеют широкое распространение при анализе динамических свойств звена (системы), например, при анализе устойчивости САР (см. раздел “Устойчивость систем автоматического управления”).

Рисунок 3.1.10 – пример ЛАХ и ФЧХ для сложной системы
Пример 1



Анализ графика в линейном масштабе по ω чаще всего не очень удобен, поскольку весь график собирается в узкой области, а дальше график абсолютной амплитуды практически сливается с 0. Если мы хотим исследовать частоты хотя бы до 1000 Гц, мы увидим практически вертикальные и горизонтальные прямые. Изменения масштаба шкалы АЧХ и ω на логарифмический дает возможность лучше исследовать частотные характеристики (см. рис. 3.1.14).
На рисунке 3.1.14 представлены частотные характеристики демпфера в логарифмическом масштабе и иллюстрация соотношения между абсолютной величиной амплитуды АФЧХ и ЛАХ в децибелах.

Пример 2
Постоим частотные характеристики для чуть более сложной модели, а именно — для гидравлического демпфера, рассмотренного в предыдущей лекции.
Для начала посмотрим на модель в виде блоков.

Частотные характеристики, получаемые в конце расчёта, приведены на рисунке 3.1.16. Видно что характеристики отличаются от простого пружинного демпфера (сравните с 3.1.14)
Блок "Построение частотных характеристик" осуществляет расчет характеристик для линеаризованной модели в окрестности заданной точки. Это означает, что частотные характеристики системы в разные моменты времени могут отличаться для нелинейных моделей. Например, в нашем случае характеристики в начале расчёта будут отличаться от характеристик, полученных в конце расчёта.
Модель гидравлического демпфера, собранного из библиотечных блоков SimInTech, представлена на рисунке 3.1.7



Использование прямого моделирования для получения характеристик является более надежным способом и работает не только с линейными моделями, но также может быть применимо для построения характеристик некоторых реальных объектов, если их можно подключить к среде моделирования и воздействовать в реальном режиме времени. Однако затраты на вычисления значительно будут больше. Например, для получения характеристик демпфера пришлось выполнить процесс в 40 000 секунд модельного времени, на обычном компьютере это заняло порядка 35 минут. График процесса перемещения плунжера в процессе вычисления характеристик приведен на рисунке 3.1.20.

Читайте также:

