Взаимное расположение двух плоскостей кратко

Обновлено: 30.06.2024

В силу аксиомы: две плоскости, имеющие общую точку, имеют общую прямую — возможны лишь два случая расположения плоскостей: 1) плоскости имеют общую прямую, т. е. пересекаются; 2) плоскости не имеют ни одной общей точки, такие плоскости называют параллельными. Существование параллельных плоскостей вытекает из следующего построения. Возьмем в плоскости (рис. 331) какие-либо две пересекающиеся прямые а и b.

Через точку М, не принадлежащую плоскости X, проведем прямые а и b, соответственно параллельные данным. Покажем, что плоскость содержащая эти прямые, параллельна плоскости . Действительно, если бы эти плоскости пересекались по некоторой прямой с, то эта прямая, принадлежа плоскости , пересекалась бы по крайней мере с одной из прямых а и такая точка пересечения была бы точкой пересечения одной из этих прямых с плоскостью . Между тем обе прямые по построению параллельны плоскости . Таким образом, предположение о пересечении плоскостей ведет к противоречию. Следовательно, плоскости параллельны. Отсюда следует

Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.

Две плоскости в пространстве могут быть параллельными или могут пересекаться, как показано в следующей таблице.

Фигура	Рисунок	Определение
Две пересекающиеся плоскости		Две плоскости называют пересекающимися , если они не совпадают, и у них есть общие точки. В случае, когда две плоскости пересекаются, пересечением этих плоскостей является прямая линия.
Две параллельные плоскости		Две плоскости называют параллельными , если они не имеют общих точек.

Определение:
Две плоскости называют пересекающимися , если они не совпадают, и у них есть общие точки. В случае, когда две плоскости пересекаются, пересечением этих плоскостей является прямая линия.

Определение:
Две плоскости называют параллельными , если они не имеют общих точек.

Признаки параллельности двух плоскостей

Первый признак параллельности двух плоскостей . Если две пересекающиеся прямые пересекающиеся прямые , лежащие в одной плоскости, соответственно параллельны параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

Доказательство . Рассмотрим рисунок 1, на котором изображены плоскости α и β

Прямые a и b лежат в плоскости α и пересекаются в точке K . Прямые c и d лежат в плоскости β и параллельны прямым a и b соответственно.

Плоскость α проходит через прямую a , параллельную прямой c , и пересекает плоскость β по прямой l . Отсюда, в силу признака параллельности прямой и плоскости, заключаем, что прямые a и l параллельны. В то же время плоскость α проходит через прямую b , параллельную прямой d , и пересекает плоскость β по прямой l . Отсюда, в силу признака параллельности прямой и плоскости, заключаем, что прямые b и l параллельны. Таким образом, мы получили, что на плоскости α через точку K проходят две прямые, а именно, прямые a и b , которые параллельны прямой l . Полученное противоречие с аксиомой о параллельных прямых аксиомой о параллельных прямых даёт возможность утверждать, что предположение о том, что плоскости α и β пересекаются, является неверным. Доказательство первого признака параллельности двух плоскостей завершено.

Второй признак параллельности двух плоскостей . Если две пересекающиеся прямые, лежащие в одной плоскости, параллельны другой плоскости, то такие плоскости параллельны.

Доказательство . Рассмотрим рисунок 3, на котором изображены плоскости α и β .

На этом рисунке также изображены прямые a и b , которые лежат в плоскости α и пересекаются в точке K. По условию каждая из прямых a и b параллельна плоскости β . Требуется доказать, что плоскости α и β параллельны.

Доказательство этого утверждения аналогично доказательству первого признака параллельности двух плоскостей, и мы его оставляем читателю в качестве полезного упражнения.

Две плоскости в пространстве могут совпадать. В этом случае они имеют, по крайней мере, три общие точки.

Две плоскости в пространстве могут пересекаться. Пересечением двух плоскостей является прямая линия, что устанавливается аксиомой: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В этом случае возникает понятие угла между пересекающимися плоскостями. Отдельный интерес представляет случай, когда угол между плоскостями равен девяноста градусам. Такие плоскости называют перпендикулярными. О них мы поговорили в статье перпендикулярность плоскостей.

Наконец, две плоскости в пространстве могут быть параллельными, то есть, не иметь общих точек. Рекомендуем ознакомиться со статьей параллельность плоскостей, чтобы получить полное представление об этом варианте взаимного расположения плоскостей.

Также интересны случаи, когда несколько плоскостей пересекаются по одной прямой и несколько плоскостей пересекаются в одной точке. О таком взаимном расположении плоскостей смотрите статьи пучок плоскостей и связка плоскостей.

Признаки параллельности прямой и плоскости:

1) Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.

2) Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.

Признаки параллельности плоскостей:

1) Если две пересекающиеся прямые одной плоскости cоответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

2) Если две плоскости перпендикулярны одной и той же прямой, то они параллельны.

Признаки перпендикулярности прямой и плоскости:

1) Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.

2) Если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.

17.Взаимные расположения прямой и плоскости в пространстве. Параллельность прямой и плоскости.

Две плоскости в пространстве могут совпадать. В этом случае они имеют, по крайней мере, три общие точки.

Признаки параллельности прямой и плоскости:

2) Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.

Признаки параллельности плоскостей:

2) Если две плоскости перпендикулярны одной и той же прямой, то они параллельны.

Признаки перпендикулярности прямой и плоскости:

2) Если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.

17.Взаимные расположения прямой и плоскости в пространстве. Параллельность прямой и плоскости.

Две различные плоскости в пространстве либо параллельны, либо пересекаются.

Параллельность двух плоскостей

Определение. Две плоскости в пространстве называются параллельными, если они не пересекаются.

Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны.

Основные свойства параллельности плоскостей.

Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
Отрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равны по длине.

Пересечение двух плоскостей

Две плоскости пересекаются по прямой. Общая прямая двух плоскостей называется ребром двугранного угла, образованного при пересечении данных плоскостей. При пересечении двух плоскостей образуются четыре двугранных угла. Если все они равны, то плоскости называются перпендикулярными.

Признак перпендикулярности плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Из признака перпендикулярности плоскостей следует, что плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

Угол между плоскостями — наименьший из двугранных углов, образованных при пересечении плоскостей.

Угловая величина двугранного угла — это величина линейного угла данного двугранного угла.

Чтобы найти линейный угол двугранного угла надо из произвольной точки на ребре двугранного угла провести в каждой плоскости по перпендикуляру к этому ребру. Все линейные углы двугранного угла равны друг другу.

Тренировочные задания

Дан куб B_C_D_" width="132" height="15" />
. Найдите угол между плоскостями C_" width="52" height="15" />
и D_C" width="54" height="15" />
.

Дан куб B_C_D_" width="132" height="15" />
. Точка — середина ребра D_" width="39" height="15" />
. Найдите угол между плоскостями " width="48" height="15" />
и " width="45" height="15" />
.

В кубе B_C_D_" width="132" height="15" />
все рёбра равны . На его ребре " width="32" height="15" />
отмечена точка так, что . Через точки и " width="18" height="15" />
построена плоскость , параллельная прямой " width="33" height="15" />
. Найдите угол наклона плоскости к плоскости грани C_C" width="65" height="15" />
.

Дана правильная треугольная призма B_C_" width="97" height="15" />
, у которой сторона основания равна , а боковое ребро равно . Через точки , " width="18" height="15" />
и середину ребра B_" width="39" height="15" />
проведена плоскость. Найдите угол между плоскостью сечения и плоскостью ABC.

Все рёбра правильной треугольной призмы B_C_" width="97" height="15" />
имеют длину . Точки и — середины рёбер " width="32" height="15" />
и C_" width="38" height="15" />
соответственно. Найдите угол между плоскостями и .

Основанием пирамиды является прямоугольник , в котором . Диагонали прямоугольника пересекаются в точке . Отрезок является высотой пирамиды . Из вершин и опущены перпендикуляры и на ребро . Найдите двугранный угол пирамиды при ребре , если .

В основании прямой призмы B_C_D_" width="132" height="15" />
лежит квадрат со стороной , а высота призмы равна . Точка лежит на диагонали " width="33" height="15" />
, причём . Найдите угол между плоскостью C_E" width="52" height="15" />
и плоскостью .

Одним из важных геометрических объектов в пространстве, который часто встречается в задачах, является плоскость. Ее математическое представление позволяет решать любые практические проблемы, которые с ней связаны.

Знание взаимного расположения двух плоскостей в пространстве является необходимым условием для понимания многих геометрических задач.

Двумерный объект в пространстве

Именно таковым является любая плоскость. Чтобы понять, как она задается, следует рассмотреть два произвольных вектора, которые не лежат на одной прямой. Сумма этих векторов, каждый из которых умножается на произвольное число, задает бесконечный набор точек в пространстве. Совокупность последних однозначно определяет изучаемый объект. Этот способ построения интуитивно понятен. Математически можно записать:

(x, y, z) = (x0, y0, z0) + α *u- + β*v-.

Здесь u- и v- - это задающие плоскость векторы, α и β - произвольные рациональные числа, которые удлиняют или укорачивают исходные направленные отрезки, (x0, y0, z0) — координаты конкретной точки в пространстве, которая однозначно определяет двумерный объект из всего их параллельного набора. Любые x, y, z, которые удовлетворяют этому выражению, относятся к рассматриваемой плоскости.

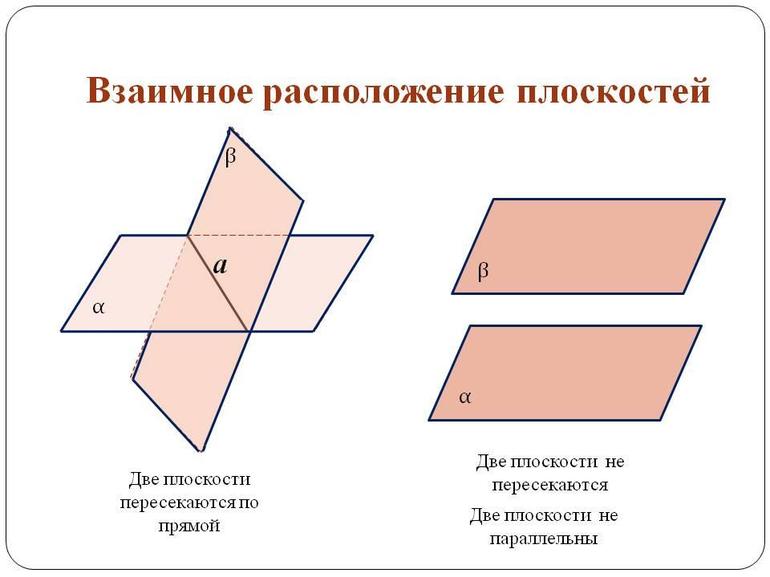
Необходимо отчетливо понимать, что изучаемый геометрический объект имеет смысл рассматривать только в трехмерном пространстве, поскольку сам он является двумерным. Например, рабочая тетрадь школьников сама по себе представляет собой единственный двумерный объект.

Нормальный вектор

Направленный отрезок, который пересекает изучаемый геометрический объект под прямым углом, называется нормальным. Соответственно, прямая, параллельная нормальному вектору, будет нормалью. Этот отрезок очень важен для понимания свойств плоскостей параллельных и пересекающихся. Кроме того, с его помощью удобно задавать сам рассматриваемый геометрический объект, при этом получается уравнение общего типа.

Если известны координаты нормали, то автоматически становится понятным, какие параллельные плоскости он задает. Их бесконечное количество. Для определения единственного объекта необходимо зафиксировать точку в пространстве, например, P0 (x0, y0, z0). Пусть P (x, y, z) также принадлежит плоскому объекту, тогда векторы PP0- и n- являются перпендикулярными, где n-(A, B, C) — нормаль. Так как следствием перпендикулярности направленных отрезков является равенство нулю их скалярного произведения, то можно записать следующее равенство:

Подставляя в него известные координаты и упрощая математическое выражение, получают следующее уравнение:

A*x + B*y + C*z + D = 0, где D = -A*x0 — B*y0 — C*z0.

Это выражение называется явным, или общего типа. Оно содержит в себе координаты нормального вектора, поэтому им легко пользоваться при решении геометрических задач.

Следует также заметить, что изменение свободного члена D приведет к параллельному переносу плоскости в пространстве. Рассматриваемый объект, у которого D=0, проходит через начало координатной системы, то есть через точку (0, 0, 0).

Математические представления

Существует несколько вариантов записи уравнений изучаемого двумерного объекта. Каждым из них удобно пользоваться при решении того или иного типа задач. Основными уравнениями являются следующие:

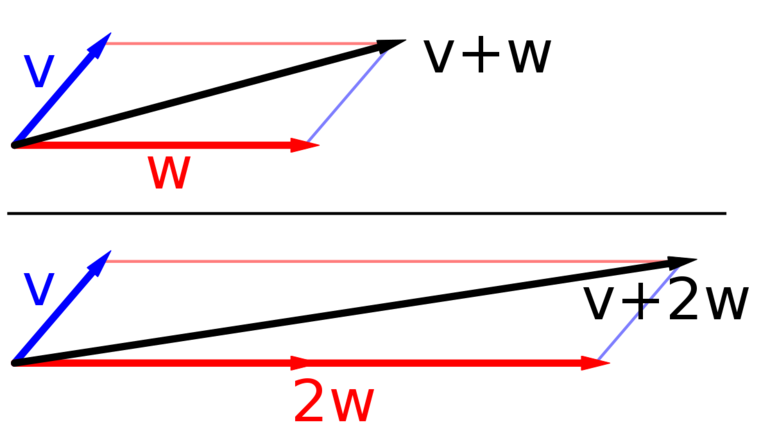
Векторное. Соответствующее ему выражение имеет вид: (x, y, z) = (x0, y0, z0) + α *u- + β*v-.
Общего типа, или явное. Его математическое выражение A*x + B*y + C*z + D = 0, где нормалью является вектор n-(A, B, C).
Параметрическое. Оно получается, если в явном виде переписать векторное представление: x = x0 + α*ux + β*vx; y = y0 + α*uy + β*vy; z = z0 + α*uz + β*vz. Здесь u (ux, uy, uz) и v (vx, vy, vz). Параметры α и β могут принимать произвольные и независимые друг от друга значения.
В отрезках. Математическая запись этого типа представления выглядит так: x/p + y/q + z/r = 1, где p, q, r — некоторые положительные или отрицательные числа. Если двумерный объект имеет представление в отрезках, то легко нарисовать его наглядное изображение на координатной плоскости, поскольку он отсекает на осях x, y и z отрезки p, q и r соответственно. Для доказательства этого утверждения достаточно положить равными нулю две координаты, например, x и z, а затем выразить из равенства третью.

На первый взгляд, четыре типа математических представлений рассматриваемого объекта могут показаться независимыми, однако это не так. Каждое представление с помощью несложных математических преобразований может быть переведено в любое другое.

Например, чтобы из явного представления получить векторное, необходимо сначала выразить какую-либо переменную из него. Затем представить через полученное выражение произвольную точку плоскости (x, y, z). После этого следует разложить правую часть равенства на три вектора, разделяя неизвестные переменные. Векторная форма получается путем вынесения за скобки двух неизвестных переменных и их последующей замены на параметры α и β.

Взаимное расположение плоскостей

Если исследовать несколько двумерных геометрических объектов в пространстве, то их можно расположить несколькими различными способами относительно друг друга. Существует в общем случае всего два принципиально отличающихся варианта:

наличие пересечения;
отсутствие пересечения.

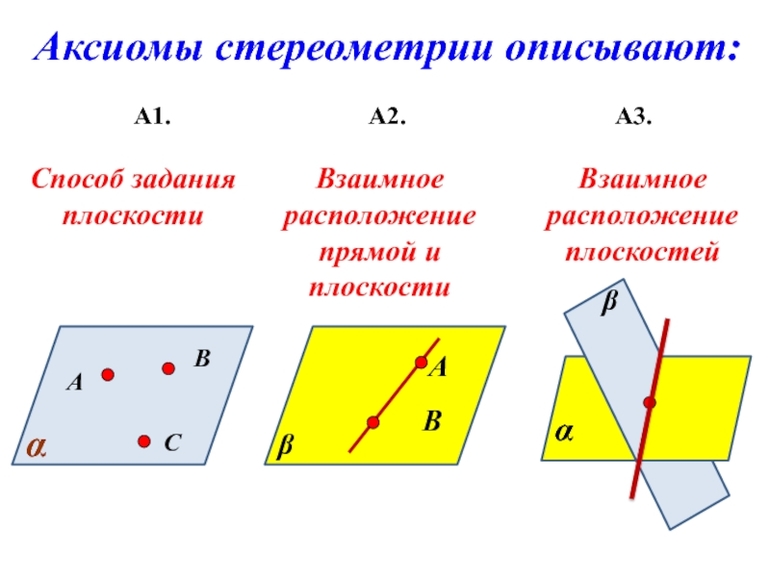
Каждый из этих случаев взаимного расположения плоскостей требует отдельного рассмотрения. Любопытно заметить, что, в отличие от прямых в пространстве, не существует накрест лежащих двумерных объектов. Если они не пересекаются, значит, являются параллельными, и наоборот.

Изучение пересечения

Для математического рассмотрения пересечения двух плоскостей удобно воспользоваться уравнением общего типа, поскольку оно в явной форме содержит координаты нормального вектора. Пусть заданы следующие две плоскости:

A1*x + B1*y + C1*z + D1 = 0;
A2*x + B2*y + C2*z + D2 = 0.

Очевидно, что они будут пересекаться тогда и только тогда, когда угол между их нормалями будет отличен от нуля. Рассчитать его можно, если воспользоваться свойством скалярного произведения векторов n1- и n2-. Искомая формула имеет следующий вид:

θ = arccos (|(A1*A2 + B1*B2 + C1*C2)|/((A1 2 +B1 2 + C1 2 )^0,5* (A2 2 +B2 2 + C2 2 )^0,5)).

Следует обратить внимание, что в числителе выражения стоит знак модуля по причине того, что угол между пересекающимися плоскостями всегда является острым.

Частным случаем является пересечение рассматриваемых объектов под углом 90°. При таком варианте расположения скалярное произведение нормальных векторов будет равно нулю ((n1*n2)=0).

Под каким бы углом ни пересекались две плоскости, происходит это строго по прямой линии. Ее уравнение можно найти, если решить систему из двух общих выражений для рассматриваемых объектов. При этом направляющий вектор прямой, по которой плоскости пересекаются, определяется как векторное произведение нормалей n1- и n2-. Очевидно, что расстояние между рассматриваемыми плоскостями всегда равно нулю, независимо от угла их пересечения.

Вопрос параллельности

Если две плоскости не пересекаются, то они всегда будут параллельными друг другу. При решении геометрических задач для доказательства параллельности можно применить один из следующих способов:

Первый: найти векторное произведение нормалей обоих объектов. Если получится нулевой результат, значит, они являются параллельными.
Второй: представить один нормальный вектор в виде умножения второго на некоторое число (если делить одну нормаль на другую покоординатно, то получится конкретное числовое значение). Если удается выполнить эту операцию, то оба вектора являются параллельными, а значит, таковыми будут и задаваемые ими плоскости.
Третий: вычислить угол между нормалями, используя свойства скалярного произведения. Если получится 0°, то рассматриваемые объекты являются параллельными.

Помимо этих трех способов, существует также признак параллельности плоскостей. Соответствующую теорему можно сформулировать следующим образом: если каждая из двух пересекающихся прямых одной плоскости параллельна соответствующей прямой для другой плоскости, то рассматриваемые двумерные объекты не имеют общих точек.

Для доказательства этого утверждения необходимо воспользоваться кратко свойством транзитивности: пара пересекающихся прямых однозначно задает нормаль плоскости. Поскольку они попарно параллельны, то нормали также будут параллельны друг другу.

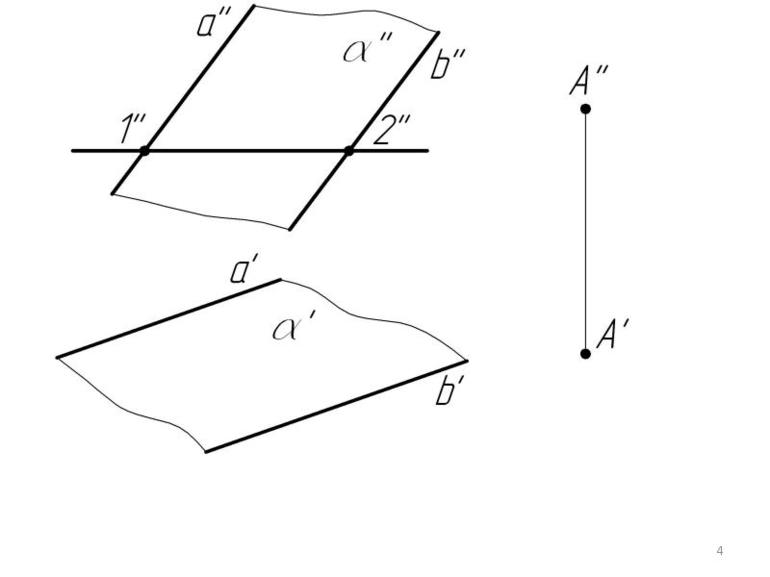
Важным свойством параллельных плоскостей является тот факт, что пересекающие их две прямые, которые параллельны друг другу, отсекают на них отрезки одинаковой длины.

Между двумя непересекающимися двумерными объектами существует определенное расстояние, которое всегда отлично от нуля. Это утверждение следует из определения параллельных плоскостей. Вычислить его можно с помощью следующей формулы:

d = |A1*x0 + B1*y0 + C1*z0 + D1|/(A1 2 + B1 2 + C1 2 )^0,5.

Здесь (x0, y0, z0) — принадлежащая второй плоскости точка.

Решение задачи

Заданы две плоскости в пространстве следующими уравнениями:

(x, y, z) = (-1,5, 0,) + α*(-2, 1, 0) + β*(1, 0, 1).

Необходимо доказать, что оба объекта являются параллельными.

Для решения этой задачи нельзя сразу воспользоваться одним из трех способов доказательства параллельности, поскольку векторное уравнение не содержит в явной форме нормальный вектор. Чтобы его получить, необходимо векторно умножить два направляющих отрезка этой плоскости:

Для получения этого результата следует воспользоваться правилом векторного умножения в матричной форме.

В свою очередь, нормаль первой плоскости имеет координаты (1, 2, -1), то есть она совпадает с нормалью для второй плоскости. Это означает, что оба двумерных объекта являются параллельными.

Таким образом, плоскости в пространстве могут либо пересекаться, либо быть параллельными. Для выполнения условия параллельности необходимо и достаточно, чтобы их нормали не пересекались, то есть угол между ними составлял 0°.

Читайте также: