Вычитание векторов кратко и понятно

Обновлено: 07.07.2024

Сложение векторов (сумма векторов) a + b есть операция вычисления вектора c , все элементы которого равны попарной сумме соответствующих элементов векторов a и b , то есть каждый элемент вектора c равен:

Вычитание векторов (разность векторов) a - b есть операция вычисления вектора c , все элементы которого равны попарной разности соответствующих элементов векторов a и b , то есть каждый элемент вектора c равен:

Формулы сложения и вычитания векторов

Формулы сложения и вычитания векторов для плоских задач

В случае плоской задачи сумму и разность векторов a = < a_x ; a_y > и b = < b_x ; b_y > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания векторов для пространчтвенных задач

В случае пространственной задачи сумму и разность векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания n -мерных векторов

В случае n -мерного пространства сумму и разность векторов a = < a ₁ ; a ₂ ; . ; a_n > и b = можно найти, воспользовавшись следующими формулами:

Примеры задач на сложение и вычитание векторов

Примеры плоских задач на сложение и вычитание векторов

Примеры пространственных задач на сложение и вычитание векторов

Примеры задач на сложение и вычитание векторов с размерностью большей 3

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

$\bar Рассмотрим два вектора и$
(рис. 1).

Разностью двух векторов и " width="8" height="16" />
называется такой третий вектор " width="9" height="11" />
, сумма которого с вектором " width="8" height="16" />
равна вектору :

$\bar-\bar =\bar\Leftrightarrow \bar+\bar=\bar$

Если задан вектор , то можно построить противоположный ему вектор , равный по длине, но противоположно направленный. Сумма противоположных векторов равна нулевому вектору:

$\bar+\left(-\bar\right)=\bar<0> $

$\bar-\bar Таким образом, разность$
можно записать в следующем виде:

$\bar-\bar =\bar+\left(-\bar\right)$

То есть разность двух векторов равна сумме уменьшаемого и вектора, противоположного вычитаемому.

Правило треугольника для разности векторов

Чтобы графически продемонстрировать разность векторов, необходимо отложить от произвольной точки вектор , из его начала вектор " width="8" height="16" />
. Тогда вектор, начало которого совпадает с концом вектора " width="8" height="16" />
, а конец – с концом вектора , и будет искомым вектором разности " width="41" height="16" />
(рис. 2).

Правило параллелограмма разности векторов

Если два неколлинеарных вектора и " width="8" height="16" />
имеют общее начало (рис. 3), то разностью этих вектор есть вектор, совпадающий с диагональю параллелограмма, построенного на этих векторах и " width="8" height="16" />
, причем начало этой диагонали совпадает с концом вектора " width="8" height="16" />
, а конец – с концом вектора .

Если векторы и " width="8" height="16" />
заданы своими координатами в некотором базисе: ;\; a_ \right),\ \bar=\left(b_ ;\; b_ \right)" width="209" height="20" />
, то, чтобы найти координаты их разности " width="41" height="16" />
, необходимо от координат вектора отнять соответствующие координаты вектора " width="8" height="16" />
:

$\bar-\bar =\left(a_ ;\; a_ \right)-\left(b_ ;\; b_ \right)=\left(a_ -b_ ;\; a_ -b_ \right)$

Примеры вычитания векторов

Задание	Найти вектор $\bar<c>=2\bar-3\bar$ , если и $\bar=\left(0;\; 2\right)$
Решение	Вначале найдем координаты векторов и $3\bar$ . Для этого умножим каждую координату векторов и $\bar$ на два и три соответственно:

$2\bar=2\cdot \left(2;\; -1\right)=\left(2\cdot 2;\; 2\cdot \left(-1\right)\right)=\left(4;\; -2\right);$

$3\bar =3\cdot \left(0;\; 2\right)=\left(3\cdot 0;\; 3\cdot 2\right)=\left(0;\; 6\right)$

Тогда искомый вектор

$\bar<c> =2\bar-3\bar=\left(4;\; -2\right)-\left(0;\; 6\right)=\left(4-0;\; -2-6\right)=\left(4;\; -8\right)$

Задание	Найти координаты вектора $\overline<AB>-\overline$ , если , , ,
Решение	Вначале найдем координаты векторов $\overline<AB>$ и $\overline$ . Для этого от координат конца вектора (точки и ) необходимо отнять соответствующие координаты его начала (точки и соответственно):

$\overline<AB> =\left(2-1;\; 3-\left(-1\right);\; -1-0\right)=\left(1;\; 4;\; -1\right),$

$\overline<CD> =\left(1-0;\; 0-\left(-1\right);\; 2-0\right)=\left(1;\; 1;\; 2\right)$

Тогда для нахождения координат вектора разности -\overline" width="83" height="16" />
, от координат вектора " width="30" height="16" />
вычтем соответствующие координаты вектора " width="31" height="16" />
:

$\overline<AB> -\overline=\left(1;\; 4;\; -1\right)-\left(1;\; 1;\; 2\right)=\left(1-1;\; 4-1;\; -1-2\right)=\left(0;\; 3;\; -3\right)$

Вычитание векторов — это арифметическое действие в геометрии, при котором из одного вектора отнимают другой.

Чтобы вычесть $\overrightarrow b$ из $\overrightarrow а$ , нужно найти такой $\overrightarrow с$ , сложение которого с вектором $\overrightarrow b$ составляло бы $\overrightarrow а$ .

Таким образом, формула разности будет выглядеть так:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

$\overrightarrow а-\overrightarrow b=\overrightarrow а+\left(-\overrightarrow b\right)$

Если задан $\overrightarrow а$ , то можно построить противоположный ему $-\overrightarrow а$ , равный по длине, но противоположно направленный. Тогда происходит сведение двух противоположно направленных векторов к нулевому:

$\overrightarrow а+\left(-\overrightarrow а\right)=0$

Как производится вычитание векторов по координатам

Если необходимо произвести вычитание векторов по координатам, то следует просто вычесть соответствующие точки. То есть если из $\overrightarrow а$ отнимается $\overrightarrow b$ , то из X₁ отнимаем X_2, из Y₁ Y₂ и из Z₁ Z₂.

Проиллюстрируем координатное пространство:

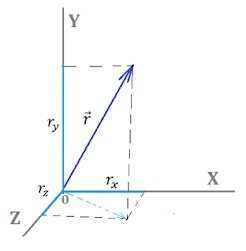
Основные правила вычисления

Для того, чтобы найти значение разности векторов, можно использовать несколько способов.

Правило треугольника

Чтобы графически продемонстрировать разность, необходимо отложить от произвольной точки вектор $\overrightarrow а$ , из его начала $\overrightarrow b$ . Тогда вектор, начало которого совпадает с концом $ \overrightarrow b$ , а конец — с концом $\overrightarrow a$ , и будет искомым вектором разности $\overrightarrow a\;-\;\overrightarrow b$ . Проиллюстрируем это:

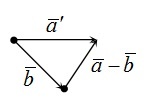
Правило параллелограмма

Если два неколлинеарных, то есть непараллельных вектора $\overrightarrow а$ и $\overrightarrow b$ имеют общее начало, то их разностью является вектор, совпадающий с диагональю параллелограмма, построенного на $\overrightarrow а$ и $\overrightarrow b$ , причем начало этой диагонали совпадает с концом $\overrightarrow b$ , а конец — с концом $\overrightarrow а$ .

Если векторы $\overrightarrow а$ и $\overrightarrow b$ заданы в некотором промежутке:

$\overrightarrow a=\left(а_1;а_2\right),\;\overrightarrow b=\left(b_1;b_2\right)$

то, чтобы найти координаты их разности $\overrightarrow a\;-\;\overrightarrow b$ , необходимо от точек $\overrightarrow a$ отнять соответствующие точки $\overrightarrow b$ :

$\overrightarrow a\;-\;\overrightarrow b=\left(a_1;a_2\right)-\left(b_1;b_2\right)=\left(a_1-b_1;a_2-b_2\right)$

Проиллюстрируем правило многоугольника:

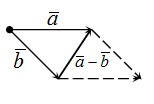
Примеры задач на понятие разности векторов

Задача 1

Дано

$\overrightarrow a\;=\left(2;-1\right),\;\overrightarrow b=\left(0;2\right)$

Найти: $\overrightarrow с=2\overrightarrow a-3\overrightarrow b\;$

Решение

Найдем координаты $2\overrightarrow a$ и $3\overrightarrow b$ . Для этого умножим каждую на два и три:

$2\overrightarrow а=2\times\left(2;-1\right)=\left(2\times2;2\times\left(-1\right)\right)=\left(4;-2\right), 3\overrightarrow b=3\times\left(0;2\right)=\left(3\times0;3\times2\right)=\left(0;6\right)$

Тогда искомый вектор:

$\overrightarrow с=2\overrightarrow a-3\overrightarrow b=\left(4;-2\right)-\left(0;6\right)=\left(4-0;\;-2-6\right)=\left(4;-8\right)$

Ответ: $\overrightarrow с=\left(4;-8\right).$

Задача 2

Дано

Найти: координаты $\overrightarrow-\overrightarrow.$

Решение

Для начала найдем проекции $\overrightarrow$ и $\overrightarrow$ .

Для этого от координат конца вектора, то есть точек B и D, нужно отнять соответствующие проекции его начала, то есть точек А и С.

Тогда для нахождения координат разности $\overrightarrow-\overrightarrow$ , от координат первого вычтем координаты второго:

В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.

Сумма векторов

Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:

Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .

Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.

Формула сложения векторов

Элементы вектора c равняются попарной сумме соответствующих элементов a и b .

" data-lang="default" data-override="" data-merged="[]" data-responsive-mode="2" data-from-history="0">

Для плоских задач	a + b = x + b_x; a_y + b_y> " data-order math"> a + b = x + b_x; a_y + b_y> " style="min-width:55.0847%; width:55.0847%;"> a + b = x + b_x; a_y + b_y>
Для трехмерных задач	a + b = x + b_x; a_y + b_y; a_z + b_z> " data-order math"> a + b = x + b_x; a_y + b_y; a_z + b_z> "> a + b = x + b_x; a_y + b_y; a_z + b_z>
Для n-мерных векторов	a + b = 1 + b₁; a₂ + b₂; . a_n + b_n> " data-order math"> a + b = 1 + b₁; a₂ + b₂; . a_n + b_n> "> a + b = 1 + b₁; a₂ + b₂; . a_n + b_n>

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: ( a + b ) + c = a + ( b + c )

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (- a ) = 0

Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:

Формула вычитания векторов

Элементы вектора c равны попарной разности соответствующих элементов a и b .

Читайте также: