Внутренние силовые факторы при изгибе кратко
Обновлено: 04.07.2024
Рассмотрим, например, балку (рис. 7.1, а), нагруженную вертикальной сосредоточенной силой (P). Для определения внутренних усилий при прямом изгибе, возникающих в поперечном сечении, расположенном на расстоянии z от места приложения нагрузки, воспользуемся методом сечений.

Разрежем мысленно балку в интересующем месте на две части.
Отбросим левую часть балки, нагруженную силой P.
Заменим действие отброшенной левой части балки на оставленную правую часть внутренними силами.
Внутренние усилия возникают во всех точках поперечного сечения балки и распределены по неизвестному закону. Не имея возможности определить эти внутренние усилия для каждой точки сечения, заменяем их статически эквивалентными внутренними силовыми факторами , приложенными в центре тяжести поперечного сечения.
Внутренние силовые факторы определяются из условия равновесия рассматриваемой части балки. Однако можем внутренние силовые факторы найти и непосредственно, как действие отброшенной левой части на правую часть. Видно, что часть балки, нагруженная силой P, стремится изогнуть рассматриваемую нами правую часть выпуклостью вниз, а также пытается произвести срез. Следовательно, в сечении должны возникнуть поперечная сила и изгибающий момент .

Осуществим параллельный перенос силы P в центр тяжести поперечного сечения балки. По правилам теоретической механики мы должны добавить момент, равный (рис. 7.1, б).
При прямом изгибе в поперечном сечении балки возникают два внутренних силовых фактора :

изгибающий момент , численно равный алгебраической сумме моментов всех сил, приложенных к отбрасываемой части балки, относительно главной центральной оси, проходящей через центр тяжести рассматриваемого сечения (в рассмотренном нами случае изгибающий момент равен: );

поперечная сила , численно равная алгебраической сумме всех внешних сил (активных и реактивных), действующих на отбрасываемую часть балки (в нашем случае поперечная сила равна: ).
Поперечный изгиб - изгиб, при котором в поперечном сечении балки возникают и изгибающий момент, и поперечная сила. Если поперечная сила не возникает, изгиб называется чистым изгибом .
Рассмотрим балку, на которую действует пара сил с моментом и внешняя сила (рис. 29.3а). Для определения внутренних силовых факторов пользуемся методом сечений.
Рассмотрим равновесие участка 1 (рис. 29.36).
Под действием внешней пары сил участок стремится развернуться по часовой стрелке. Силы упругости, возникающие в сечении 1, удерживают участок в равновесии.
Продольные силы упругости выше оси бруса направлены налево, а силы ниже оси направлены направо. Таким образом, при равновесии участка 1 получим: . Продольная сила в сечении равна нулю. Момент сил упругости относительно оси может быть получен, если суммировать элементарные моменты сил упругости в сечении 1-1 относительно оси :


Этот момент называют изгибающим моментом .


Из схемы вала на рис. 29.36 видно, что часть волокон (выше оси) испытывают сжатие, а волокна ниже оси растянуты. Следовательно, в сечении должен существовать слой не растянутый и не сжатый, где напряжения равны нулю.
Такой слой называют нейтральным слоем (НС). Линия пересечения нейтрального слоя с плоскостью поперечного сечения бруса называют нейтральной осью.

Нейтральный слой проходит через центр тяжести сечения. Здесь нейтральный слой совпадает с осью .
Практически величина изгибающего момента в сечении определяется из уравнения равновесия:

Таким образом, в сечении 1-1 продольная сила равна нулю, изгибающий момент в сечении постоянен.
Изгиб, при котором в поперечном сечении бруса возникает только изгибающий момент, называется чистым изгибом.
Рассмотрим равновесие участка бруса от свободного конца до сечения 2 (рис. 29.3в).
Запишем уравнения равновесия для участка бруса:

В сечении бруса 2-2 действует поперечная сила, вызывающая сдвиг.

Изгибающий момент в сечении:


— расстояние от сечения 2 до начала координат.
Изгибающий момент зависит от расстояния сечения до начала координат.
Изгиб, при котором в поперечном сечении бруса возникает изгибающий момент и поперечная сила, называется поперечным изгибом.
Возможно эти страницы вам будут полезны:





















































Образовательный сайт для студентов и школьников
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Брус, работающий на изгиб, называют балкой.
Изображен брус, закрепленный справа (защемление), нагруженный внешними силами и моментом (рис. 29.1).
Плоскость, в которой расположены внешние силы и моменты, называют силовой плоскостью.
Если все силы лежат в одной плоскости, изгиб называют плоским.
Плоскость, проходящая через продольную ось бруса и одну из главных осей его центральных поперечного сечения, называется главной плоскостью бруса.
Если силовая плоскость совпадает с главной плоскостью бруса, изгиб называют прямым (рис. 29.1).
Если силовая плоскость не проходит через главную плоскость бруса, изгиб называют косым изгибом (рис. 29.2).

Внутренние силовые факторы при изгибе
Пример 1.Рассмотрим балку, на которую действует пара сил с моментом ти внешняя сила F (рис. 29.3а). Для определения внутренних силовых факторов пользуемся методом сечений.
Рассмотрим равновесие участка 1 (рис. 29.36).
Под действием внешней пары сил участок стремится развернуться по часовой стрелке. Силы упругости, возникающие в сечении 1, удерживают участок в равновесии.
Продольные силы упругости выше оси бруса направлены направо ,
Тема 2.6. Изгиб. Классификация видов изгиба 241
а силы ниже оси направлены налево. Таким образом, при равновесии участка 1 получим: ΣFZ = 0. Продольная сила N в сечении равна нулю. Момент сил упругости относительно оси Ох может быть получен, если суммировать элементарные моменты сил упругости в сечении 1-1 относительно оси Ох:

Этот момент называют изгибающим моментом Мх = Ми.

Из схемы вала на рис. 29.3b видно, что часть волокон (выше оси) испытывают сжатие, а волокна ниже оси растянуты. Следовательно, в сечении должен существовать слой не растянутый и не сжатый, где напряжения σ равны нулю.
Такой слой называют нейтральным слоем (НС). Линия пересечения нейтрального слоя с плоскостью поперечного сечения бруса называют нейтральной осью.
Нейтральный слой проходит через центр тяжести сечения. Здесь нейтральный слой совпадает с осью Ох.

Практически величина изгибающего момента в сечении определяется из уравнения равновесия:
Таким образом, в сечении 1-1 продольная сила равна нулю, изгибающий момент в сечении постоянен.
Изгиб, при котором в поперечном сечении бруса возникает только изгибающий момент, называется чистым изгибом.
Рассмотрим равновесие участка бруса от свободного конца до сечения 2 (рис. 29.3в).
Запишем уравнения равновесия для участка бруса:


В сечении бруса 2-2 действует поперечная сила, вызывающая сдвиг.
Изгибающий момент в сечении: МХ2 = т - F(z2 — a);
z2 — расстояние от сечения 2 до начала координат.
Изгибающий момент зависит от расстояния сечения до начала координат.
Изгиб, при котором в поперечном сечении бруса возникает изгибающий момент и поперечная сила, называется поперечным изгибом.
Как оформить тьютора для ребенка законодательно: Условием успешного процесса адаптации ребенка может стать.
Основные признаки растений: В современном мире насчитывают более 550 тыс. видов растений. Они составляют около.
Плоский поперечный изгиб прямых стержней (брусьев, балок). Определение внутренних сил (поперечных сил и изгибающих моментов) в произвольном поперечном сечении стержня и построение их эпюр. Дифференциальные зависимости между нагрузкой, поперечными силами, изгибающими моментами, их использование при построении диаграмм и контроля правильности построения.
Плоский изгиб. Под плоским поперечным изгибом понимают такой вид деформации, при которой происходит искривление оси прямого бруса, и в поперечном сечении бруса действует два силовых фактора: изгибающий момент М и поперечная сила Q. Осью бруса называется геометрическое место точек центров тяжестей поперечных сечений бруса. Изгиб – плоский, если ось балки после деформации остается плоской линией. В противном случае имеет место косой изгиб. Если поперечная сила не возникает, изгиб называется чистым изгибом.
Рассмотрим, например, балку, нагруженную вертикальной сосредоточенной силой P. Для определения внутренних усилий при прямом изгибе, возникающих в поперечном сечении, расположенном на расстоянии z от места приложения нагрузки, воспользуемся методом сечений.


Рис. 22. Плоский изгиб:
а – балка под нагрузкой Р; б – внутренние силы при изгибе
Разрежем мысленно балку в интересующем месте на две части.Отбросим левую часть балки, нагруженную силой P. Заменим действие отброшенной левой части балки на оставленную правую часть внутренними силами.
Внутренние усилия возникают во всех точках поперечного сечения балки и распределены по неизвестному закону. Не имея возможности определить эти внутренние усилия для каждой точки сечения, заменяем их статически эквивалентными внутренними силовыми факторами, приложенными в центре тяжести поперечного сечения.
Внутренние силовые факторы определяются из условия равновесия рассматриваемой части балки. Однако можем внутренние силовые факторы найти и непосредственно, как действие отброшенной левой части на правую часть. Видно, что часть балки, нагруженная силой P, стремится изогнуть рассматриваемую нами правую часть выпуклостью вниз, а также пытается произвести срез. Следовательно, в сечении должны возникнуть поперечная сила и изгибающий момент.
Осуществим параллельный перенос силы P в центр тяжести поперечного сечения балки. По правилам теоретической механики добавляется момент, равный Pz.
Таким образом, в поперечном сечении балки возникают два внутренних силовых фактора:
– изгибающий момент, численно равный алгебраической сумме моментов всех сил, приложенных к отбрасываемой части балки, относительно главной центральной оси, проходящей через центр тяжести рассматриваемого сечения (в данном примере М = Рz);
– поперечная сила, численно равная алгебраической сумме всех внешних сил (активных и реактивных), действующих на отбрасываемую часть балки (в нашем примере Q = P).
Построение эпюр поперечных сил и изгибающих моментов. При расчете балок на прочность необходимо знать характер изменения изгибающего момента и поперечной силы вдоль оси балки и знать положение опасного сечения. С этой целью строят эпюры поперечных сил и изгибающих моментов.
Если внешняя сила стремится повернуть отсеченную часть по часовой стрелке относительно рассматриваемого сечения, то поперечная сила положительна.


Рис. 23. Правило знаков для внутренних усилий:
а – для поперечной силы; б – для изгибающего момента
Изгибающий момент будет положительным, если при действии момента внешних сил балка искривляется выпуклостью вниз.
Построение эпюр поперечных сил и изгибающих моментов рассмотрим на конкретном примере.
Пусть на балку действует внешний изгибающий момент m = 6 кН•м и внешняя сила F = 12 кН, l = 1 м. Определим реакции в опорах A и B. Составим уравнения равновесия моментов всех внешних сил относительно опор A и B



Рис. 24. Эпюры Qy, Mx
Проведем сечения на каждом характерном участке и определим значения поперечной силы Qy и изгибающего момента Mx.
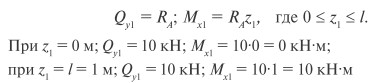
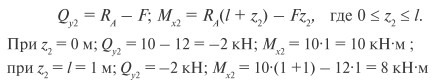
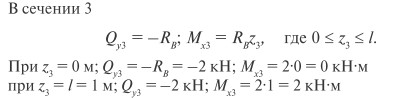
По полученным значениям строим эпюры поперечных сил и изгибающих моментов (рис. 24).
Дифференциальные зависимости при изгибе.
Выделим на участке балки с произвольной нагрузкой в месте, где нет сосредоточенных сил и моментов, малый элемент dz. Так как вся балка находится в равновесии, то и элемент dz будет находиться в равновесии под действием приложенных к нему поперечных сил, изгибающих моментов и внешней нагрузки. Поскольку Qy и Mx в общем случае меняются вдоль оси балки, то в сечениях элемента dz будут возникать поперечные силы Qy и Qy + dQy, а также изгибающие моменты Mx и Mx + dMx.
Из условия равновесия выделенного элемента получим:

следовательно


следовательно

Первое из двух записанных уравнений дает условие

(10)

Из второго уравнения, пренебрегая слагаемым как бесконечно малой величиной второго порядка, найдем

(11)
Рассматривая полученные выражения, совместно можем получить

(12)
Полученные соотношения называют дифференциальными зависимостями Д.И. Журавского при изгибе.


Рис. 25. Внутренние усилия в балке при изгибе
Анализ дифференциальных зависимостей при изгибе позволяет установить некоторые правила построения эпюр изгибающих моментов и поперечных сил:
– на участках, где нет распределенной нагрузки q, эпюры Q ограничены прямыми, параллельными базе, а эпюры М – наклонными прямыми;
– на участках, где к балке приложена распределенная нагрузка q, эпюры Q ограничены наклонными прямыми, а эпюры М – квадратичными параболами;
– в сечениях, где к балке прикладывается сосредоточенная сила, на эпюре Q будут скачки на величину и в направлении данной силы, а на эпюре М – перегибы, острием направленные в направлении действия этой силы;
– в сечениях, где к балке прикладывается сосредоточенный момент, на эпюре Q изменений не будет, а на эпюре М – скачок на величину момента;
– в сечении, где приложена сосредоточенная внешняя сила эпюра изгибающих моментов делает резкое изменение угла наклона смежных участков эпюры (излом эпюры). Излом эпюры направлен навстречу вектору силы;
– сосредоточенная (или распределенная) пара сил влияния на закон изменения поперечных сил на участке не оказывает, и на эпюре Q это ни как не отражается;
– в сечении, где приложена пара сил, эпюра изгибающих моментов делает скачок на величину этой пары и с ее знаком;
– на участке, где приложена равномерно распределенная нагрузка q, эпюра поперечных сил имеет вид прямой наклонной линии с угловым коэффициентом q;

Рис. 26. В сечении, в котором к балке приложена сосредоточенная внешняя сила, перпендикулярная к оси балки, эпюра поперечных сил Q делает скачок
на величину этой силы и с ее знаком
– на участке, где приложена равномерно распределенная нагрузка, эпюра изгибающих моментов ограничена параболической кривой;
– в сечении, где приложена сосредоточенная сила, эпюра изгибающих моментов делает резкое изменение угла наклона смежных участков эпюры (излом эпюры). Излом эпюры направлен навстречу вектору силы;
– на участке, где поперечная сила равна нулю, наблюдается деформация чистого плоского изгиба, при котором изгибающий момент является постоянной величиной.
Читайте также:

