Уравнение максвелла для электромагнитного поля кратко

Обновлено: 05.07.2024

Уравнения Максвелла — основная идея и физическая суть

Закономерности, выведенные Максвеллом, в электродинамике имеют такое значение, как, к примеру, законы Ньютона для классической механики и постулаты Эйнштейна в теории относительности. Это фундаментальные уравнения, которые подтверждены экспериментальным путем.

Уравнения Максвелла являются системой уравнений в дифференциальном или интегральном виде, которые описывают любые электромагнитные поля, взаимосвязи токов и электрических зарядов в разных средах, включая вакуум.

Уравнения Максвелла подвергались критике со стороны современников ученого, так как не вписывались в установленные стандарты и представления того времени. Однако закономерности послужили началом активного развития науки и причиной переворота в восприятии картины мира. Постулаты предшествовали открытию радиоволн и продемонстрировали электромагнитную природу света. Формулы Максвелла справедливы для макромира и области квантовой механики.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Что описывают четыре уравнения

Из первой закономерности рассматривается поток электрического поля Е сквозь какую-либо поверхность замкнутого типа. Можно наблюдать зависимость между потоком и суммарным зарядом. Уравнение является законом или теоремой Гаусса.
Второе уравнение Максвелла выражает закон Фарадея, на основе которого функционируют электрические моторы. В двигателях возникает ток в катушке в процессе вращения магнита.
Третье уравнение Максвелла также представляет собой закон Гаусса, но в рамках электрического поля. В этом случае для потока магнитного поля будет характерно нулевое значение. Положительные и отрицательные заряды существуют отдельно друг от друга и порождают вблизи электрическое поле, а магнитные заряды — отсутствуют в природе.
Четвертый постулат Максвелла имеет наибольшее значение. Исходя из уравнения, был введен термин тока смещения. Данная формула получила название теоремы о циркуляции вектора магнитной индукции. Согласно этому утверждению, вихревое магнитное поле образовано электрическим током и изменением электрического поля.

Смысл уравнений Максвелла:

Первое уравнение — электрическое поле сформировано электрическим зарядом.
Второе уравнение — вихревое электрическое поле формируется в результате изменений магнитного поля.
Третье уравнение — магнитные заряды отсутствуют в природе.
Четвертое уравнение — вихревое магнитное поле является результатом электрического тока и изменений электрической индукции.

Как записать в интегральной форме

Первое уравнение

Первое уравнение Максвелла представляет собой дифференциальную формулировку закона полного тока. Формула выглядит следующим образом:

S опирается на контур L.

Согласно теореме Стокса:

Уравнение справедливо для любых поверхностей, которые опираются на материальный контур L. Исходя из этого, подынтегральные функции равны.

Данная формула является дифференциальной формой закона Ома.

Первое уравнение Максвелла имеет вид:

Физический смысл данной расшифровки заключается в том, что в качестве источников вихревых магнитных полей выступают токи проводимости и токи смещения.

Второе уравнение

Второе уравнение Максвелла представляет собой дифференциальную формулировку закона электромагнитной индукции и ее свойств:

Второе уравнение Максвелла имеет следующий вид:

Физический смысл заключается в том, что переменное электрическое поле создается вихревым электрическим полем.

Третье уравнение

Третье уравнение Максвелла представляет собой дифференциальную формулировку теоремы Гаусса для электрических полей:

С помощью теоремы Островского-Гаусса можно выполнить переход от поверхностного интеграла \( \left(\vec \right)\) к объемному интегралу ( \(div D\) ):

Можно записать правую часть формулы для объемного заряда. После объединения двух уравнений получим:

Третье уравнение Максвелла:

Физический смысл закономерности заключается в том, что электрическое поле образовано источниками в виде зарядов с определенной плотностью.

Четвертое уравнение

Четвертым уравнением Максвелла является дифференциальная формулировка теоремы Гаусса, справедливая в условиях магнитного поля:

Четвертое уравнение Максвелла имеет вид:

Физический смысл четвертого уравнения Максвелла выражается в нулевом значении дивергенции вектора \(\vec\) для какой-либо точки в пространстве. Таким образом, сделан вывод об отсутствии источников или магнитных зарядов в природе.

Закон сохранения заряда в дифференциальной форме

Данная формула имеет следующий вид:

С помощью теоремы Островского-Гаусс можно вывести уравнение, которое будет являться результатов предыдущих закономерностей:

В основе теории Максвелла лежат рассмотренные выше четыре уравнения:

1. Электрическое поле может быть как потенциальным (Е_Q), так и вихревым (Е_B), поэтому напряженность суммарного поля Е=Е_Q +Е_B. Так как циркуляция вектора Е_Q равна нулю (см. (137.3)), а циркуляция вектора Е_B определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):

Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля D (см. (89.3)):

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, то формула (139.1) запишется в виде

4. Теорема Гаусса для поля В (см. (120.3)):

Итак, полная система уравнений Максвелла в интегральной форме:

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

где e₀ и m₀ — соответственно электрическая и магнитная постоянные, e и m — соответственно диэлектрическая и магнитная проницаемости, g — удельная проводимость вещества.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид

т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.

Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.

Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше:

(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).

Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.

Ток смещения или абсорбционный ток — величина, прямо пропорциональная быстроте изменения электрической индукции. Это понятие используется вклассической электродинамике

. Введено Дж. К. Максвеллом при построении теории электромагнитного поля.

Введение тока смещения позволило устранить противоречие [1] в формуле Ампера для циркуляции магнитного поля, которая после добавления туда тока смещения стала непротиворечивой и составила последнее уравнение, позволившее корректно замкнуть систему уравнений (классической) электродинамики.

Строго говоря, ток смещения не является [2] электрическим током, но измеряется в тех же единицах, что и электрический ток.

ного коэффициента) называется [3] поток вектора быстроты изменения электрического поля через некоторую поверхность [4] :

В основе теории Максвелла лежат рассмотренные выше четыре уравнения:

2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):

3. Теорема Гаусса для поля D (см. (89.3)):

4. Теорема Гаусса для поля В (см. (120.3)):

Итак, полная система уравнений Максвелла в интегральной форме:

Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид

Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

. Введено Дж. К. Максвеллом при построении теории электромагнитного поля.

Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.

Полезная и интересная информация по другим темам – у нас в телеграм.

Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.

Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.

Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

По порядку запишем и поясним все 4 уравнения. Сразу уточним, что записывать их будем в системе СИ.

Первое уравнение Максвелла

Современный вид первого уравнения Максвелла таков:

Тут нужно пояснить, что такое дивергенция. Дивергенция – это дифференциальный оператор, определяющий поток какого-то поля через определенную поверхность. Уместным будет сравнение с краном или с трубой. Например, чем больше диаметр носика крана и напор в трубе, тем большим будет поток воды через поверхность, которую представляет собой носик.

Так вот, поток электрического поля E через любую замкнутую поверхность зависит от суммарного заряда внутри этой поверхности. Данное уравнение представляет собой закон (теорему) Гаусса.

Третье уравнение Максвелла

Сейчас мы пропустим второе уравнение, так как третье уравнение Максвелла – это тоже закон Гаусса, только уже не для электрического поля, но для магнитного.

Что это значит? Поток магнитного поля через замкнутую поверхность равен нулю. Если электрические заряды (положительные и отрицательные) вполне могут существовать по отдельности, порождая вокруг себя электрическое поле, то магнитных зарядов в природе просто не существует.

Второе уравнение Максвелла

Второе уравнение Максвелла представляет собой ни что иное, как закон Фарадея. Его вид:

Ротор электрического поля (интеграл через замкнутую поверхность) равен скорости изменения магнитного потока, пронизывающего эту поверхность. Чтобы лучше понять, возьмем воду в ванной, которая сливается через отверстие. Вокруг отверстия образуется воронка. Ротор – это сумма (интеграл) векторов скоростей частиц воды, которые вращаются вокруг отверстия.

Как Вы помните, на основе закона Фарадея работают электродвигатели: вращающийся магнит порождает ток в катушке.

Четвертое уравнение Максвелла

Четвертое - самое важное из всех уравнений Максвелла. Именно в нем ученый ввел понятие тока смещения.

Это уравнение еще называется теоремой о циркуляции вектора магнитной индукции. Оно говорит нам о том, что электрический ток и изменение электрического поля порождают вихревое магнитное поле.

Приведем теперь всю систему уравнений и кратко обозначим суть каждого из них:

Первое уравнение: электрический заряд порождает электрическое поле

Второе уравнение: изменяющееся магнитное поле порождает вихревое электрическое поле

Третье уравнение: магнитных зарядов не существует

Четвертое уравнение: электрический ток и изменение электрической индукции порождают вихревое магнитное поле

Решая уравнения Максвелла для свободной электромагнитной волны, мы получим следующую картину ее распространения в пространстве:

Надеемся, эта статья поможет систематизировать знания об уравнениях Максвелла. А если понадобиться решить задачу по электродинамике с применением этих уравнений, можете смело обратиться за помощью в студенческий сервис. Подробное объяснение любого задания и отличная оценка гарантированы.

Уравнения Максвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь сэлектрическими зарядами и токами в вакууме и сплошных средах.

Основу теории Максвелла составляют четыре структурных уравнения, которые записываются в интегральной и дифференциальной формах. В интегральной форме они выражают соотношения для мысленно проведенных в ЭМП контуров и замкнутых поверхностей, а в дифференциальной – показывают, как связаны между собой характеристики ЭМП и плотности электрических зарядов и токов в каждой точке пространства.

Дифференциальная форма

Уравнения Максвелла представляют собой в векторной записи систему из четырех уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных) линейных дифференциальных уравнений в частных производных 1-го порядка для 12 компонент четырёх векторных функций ( ):

Название	СИ	Примерное словесное выражение
Закон Гаусса		Электрический заряд является источником электрической индукции.
Закон Гаусса для магнитного поля		Не существует магнитных зарядов.
Закон индукции Фарадея		Изменение магнитной индукции порождает вихревое электрическое поле.
Теорема о циркуляции магнитного поля		Электрический ток и изменение электрической индукции порождают вихревое магнитное поле

Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.

Введённые обозначения:

— плотность стороннего электрического заряда (в единицах СИ — Кл/м³);

— плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае - случае тока, порождаемого одним типом носителей заряда, она выражается просто как , где — (средняя) скорость движения этих носителей в окрестности данной точки, ρ₁ - плотность заряда этого типа носителей (она в общем случае не совпадает с ρ); в общем случае это выражение надо усреднить по разным типам носителей;

— скорость света в вакууме (299 792 458 м/с);

— напряжённость электрического поля (в единицах СИ — В/м);

— напряжённость магнитного поля (в единицах СИ — А/м);

— электрическая индукция (в единицах СИ — Кл/м²);

— магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с −2 •А −1 );

— дифференциальный оператор набла, при этом:

означает ротор вектора,

означает дивергенцию вектора.

Интегральная форма

При помощи формул Остроградского-Гаусса и Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:

Название	СИ	Примерное словесное выражение
Закон Гаусса		Поток электрической индукции через замкнутую поверхность sпропорционален величине свободного заряда, находящегося в объёме v, который окружает поверхность s.
Закон Гаусса для магнитного поля		Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют).
Закон индукции Фарадея		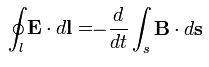Изменение потока магнитной индукции, проходящего через незамкнутую поверхностьs, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре l, который является границей поверхности s.
Теорема о циркуляции магнитного поля		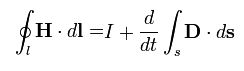Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность s, пропорциональны циркуляции магнитного поля на замкнутом контуре l, который является границей поверхности s.

Введённые обозначения:

— двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объём , и открытая поверхность в случае законов Фарадея и Ампера-Максвелла (её границей является замкнутый контур ).

— электрический заряд, заключённый в объёме , ограниченном поверхностью (в единицах СИ — Кл);

— электрический ток, проходящий через поверхность (в единицах СИ — А).

Полная система уравнений Максвелла для электромагнитных полей

Данные четыре структурных уравнения дополняются тремя материальными уравнениями, характеризующими свойства среды. Для изотропных несегнетоэлектрических и неферромагнитных сред материальные уравнения имеют вид, соответственно

Читайте также: