Свойства треугольника паскаля кратко

Обновлено: 30.06.2024

Таблица П. – Натуральные степени бинома x + y

№	Степень	Разложение в сумму одночленов
0	(x + y) 0 =	1
1	(x + y) 1 =	1x + 1y
2	(x + y) 2 =	1x 2 + 2xy + 1y 2
3	(x + y) 3 =	1x 3 + 3x 2 y + 3xy 2 + 1y 3
4	(x + y) 4 =	1x 4 + 4x 3 y + 6x 2 y 2 + 4xy 3 + 1y 4
5	(x + y) 5 =	1x 5 + 5x 4 y + 10x 3 y 2 + 10x 2 y 3 + 5xy 4 + 1y 5
6	(x + y) 6 =	1x 6 + 6x 5 y + 15x 4 y 2 + 20x 3 y 3 + + 15x 2 y 4 + 6xy 5 + 1y 6
…	…	…

Теперь, воспользовавшись третьим столбцом Таблицы П., составим следующую Таблицу - Треугольник Паскаля:

Разложение в сумму одночленов:

Теперь, записыая только коэффициенты разложений степеней бинома в сумму одночленов, получим следующую Таблицу - Треугольник Паскаля:

Таблица - Треугольник Паскаля

№	Треугольник Паскаля
0	1
1	1 1
2	1 2 1
3	1 3 3 1
4	1 4 6 4 1
5	1 5 10 10 5 1
6	1 6 15 20 15 6 1
…	…

На всякий случай напомним, что Блез Паскаль – это знаменитый физик и математик, живший во Франции более трех веков назад.

В треугольнике Паскаля каждая строка соответствует строке с тем же номером в Таблице П. Однако в каждой строке треугольника Паскаля, в отличие от Таблицы П., записаны только коэффициенты разложения в сумму одночленов соответствующей степени бинома x + y .

Заполнив сначала строки треугольника Паскаля с номерами 0 и 1, рассмотрим строки с номерами 2 и далее.

Основным свойством треугольника Паскаля , позволяющим последовательно, начиная со строки с номером 2, заполнять его строки, является следующее свойство:

Каждая из строк, начиная со строки с номером 2, во-первых, начинается и заканчивается числом 1, а, во-вторых, между числами 1 стоят числа, каждое из которых равно сумме двух чисел, стоящих над ним в предыдущей строке.

Действительно, число 2, стоящее в строке с номером два, равно сумме чисел 1 плюс 1, стоящих в первой строке. Точно так же, числа 3 и 3, стоящие в строке с номером три, равны соответственно сумме чисел 1 плюс 2 и сумме чисел 2 плюс 1, стоящих во второй строке.

Также и для других строк.

Таким образом, свойство треугольника Паскаля позволяет, заполнив одну из строк, легко заполнить и следующую за ней, т.е. получить необходимые коэффициенты разложения в сумму одночленов следующей степени бинома x + y .

Пример . Написать разложение вида:

Решение . Воспользовавшись строкой треугольника Паскаля с номером 6 и применив основное свойство треугольника Паскаля, получим строку с номером 7:

Треугольник Паскаля можно обобщить на большие измерения . Трехмерная версия называется пирамидой Паскаля или тетраэдром Паскаля , а более общие версии называются симплексом Паскаля . [ требуется ссылка ]

История

Первое явное представление треугольника биномиальных коэффициентов датируется 10 веком , в комментариях к Чандас Шастре , древней индийской книге санскритской просодии , написанной Пингалой около 200 г. до н.э. [ 3 ]

Свойства треугольника обсуждались персидскими математиками Аль-Караджи (953–1029) [ 4 ] и Омаром Хайямом (1048–1131); следовательно, в Иране он известен как треугольник Хайяма-Паскаля или просто треугольник Хайяма . Также были известны многие родственные теоремы, в том числе биномиальная теорема .

В Китае этот треугольник был известен с XI века китайским математиком Цзя Сянем (1010–1070). В 13 веке Ян Хуэй (1238—1298) представил арифметический треугольник , эквивалентный треугольнику Паскаля, поэтому в Китае его называют треугольником Ян Хуэй . [ 5 ] [ 6 ] [ 7 ] [ 8 ]

Петрус Апианус (1495–1552) опубликовал треугольник на обложке своей книги по коммерческим расчетам Rechnung [ 9 ] (1527). Это первая запись треугольника в Европе. В Италии он известен как Треугольник Тартальи в честь итальянского алгебраиста Никколо Фонтана Тартальи (1500–1577). Его также изучали Майкл Штифель (1486–1567) [ 10 ] и Франсуа Виет (1540–1603).

Строительство

Общее использование

Этот треугольник был придуман для развития способностей биномов . Степени двучленов задаются формулой :, где a и b — любые переменные , а n — показатель степени , определяющий степень. Это выражение называется биномом Ньютона . ( а + б ) н >

Эта биномиальная формула Ньютона развивает коэффициенты каждой строки в треугольнике Паскаля. Вот почему существует тесная связь между треугольником Паскаля и биномом Ньютона .

Связь между треугольником Паскаля и биномом Ньютона

Все цифры, написанные в каждой строке треугольника, соответствуют коэффициентам развития степеней бинома Ньютона. Вот несколько примеров из серии, описывающих такое поведение:

С помощью этих примеров делается вывод, что ряд общего выражения, которое их развивает, таков:

Этот результат можно также обобщить на любое значение по математической индукции . н е Н >

Если мы обозначим каждый узел этого треугольника в каждой строке z , мы получим ряд, описывающий общее выражение режима:

( а + б ) н знак равно с участием 1 а н + с участием 2 а н − 1 б + с участием 3 а н − 2 б 2 . . . + с участием н б н = z_ a ^ + z_ a ^ b + z_ a ^ b ^ < 2>. +z_b^>

В этом ряду , где z идет от 1 до n . с участием е Н >

Комбинаторика в треугольнике Паскаля

Все это предположение о корреляции между комбинаторикой и треугольником Паскаля дается вышеупомянутым общим правилом:

Например, для бинома у нас будет следующее: ( а + б ) 3 >

В разработанном уравнении бинома будет четыре узла (элементы, состоящие из a , b и соответствующего коэффициента) , число которых относится к строке, в которой оно находится:

Если выразить коэффициенты треугольника в комбинаторной форме, останется следующее:

Свойства (изменить)

Треугольник Паскаля с несколькими цветными квадратами. Видно, как значения распределяются симметрично вокруг вертикальной оси. Значения ячеек с обеих сторон (желтой, зеленой и красной) имеют одинаковое значение благодаря свойству симметрии . Внешние прямоугольники (синие) имеют нулевое значение, а квадраты фиолетового цвета представляют собой пример правила Паскаля. ( n n − p ) = ( n p ) >=>

Как только будут заложены основы внутренней корреляции, существующей между этими двумя областями математики, см. их свойства.

Значения каждой строки треугольника симметричны относительно его мнимой вертикальной оси, потому что ( n n − p ) = ( n p ) . >=
>.>

Значения, соответствующие площади вне треугольника, имеют значение 0 , так как когда . ( n p ) = 0
>=0> p > n n>

И, конечно же, правило Паскаля для построения треугольника дает фундаментальное соотношение биномиальных коэффициентов ( n p ) + ( n p + 1 ) = ( n + 1 p + 1 ) .
>+>=>.>

Интересным следствием треугольника Паскаля является то, что сумма всех значений в любой одной строке треугольника является степенью числа 2 . Это связано с тем, что по биномиальной теореме разложение n -степени равно ( 1 + 1 ) n = 2 n =2^>

что в точности соответствует сумме всех значений n -й строки треугольника Паскаля.

Аппроксимация треугольника Серпинского, полученная окрашиванием ячеек треугольника Паскаля, содержащих четное число, в черный цвет, а тех, которые содержат нечетное число, в серый цвет.

Другие интерпретации или представления

Прямоугольный треугольник

Каждое число в любом столбце равно частичной сумме элементов из предыдущего столбца (слева) до предыдущей строки в порядке убывания.
Третий столбец — это последовательность треугольных чисел; четвертая — тетраэдрические числа ; пятая — пятигранных чисел и так далее .

Полномочия в базе 2

Степени по основанию 2 также можно найти в виде последовательных сумм коэффициентов строк, где n - строка, в которой находится мощность : 2 n , n ∈ N ,\ n\in \mathbb > 2 n >

Последовательность Фибоначчи

В треугольнике Паскаля можно увидеть связь между способом сложения диагоналей и последовательностью Фибоначчи . Первые члены этой последовательности: 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 …

Как видно на изображении справа, последовательные суммы диагоналей от верхнего правого до нижнего левого составляют последовательность Фибоначчи.

простые числа

55, 165, 330 и 462 делятся на 11.

Обобщения

Вместо того, чтобы рассматривать степени a + b , мы можем рассмотреть степени трехчлена a + b + c . Таким образом, ( a + b + c ) n представляет собой сумму мономов вида λ _{p , q , r} a p b q c r , где p , q и r положительные , p + q + r = n , а λp _, _q _, _{r —} натуральное число, называемое трехчленным коэффициентом . [ 12 ] [ 13 ] Расчеты аналогичны расчетам биномиального коэффициента и задаются следующим выражением:

в подмножествах p , q и r элементов.

Эти коэффициенты можно рассматривать как трехмерную аналогию треугольника Паскаля. На самом деле распределение этих коэффициентов в пирамидальном стиле известно как пирамида Паскаля ; он также бесконечен , с треугольными секциями, и значение в каждом поле представляет собой сумму значений трех полей над ним.

В этой пирамиде наблюдается инвариант поворота на 120 градусов вокруг вертикальной оси, проходящей через вершину. Треугольник Паскаля появляется на всех трех гранях пирамиды.

Смотрите также

Примечания и ссылки

внешняя ссылка

в магазине \(7\) разных маек. Галя хочет примерить \(2\) майки, а Аня хочет примерить \(5\). Сколько существует возможностей для каждой из девочек каждый раз выбрать новый комплект для примерки?

У Гали C 7 2 = 7 ! 2 ! 7 − 2 ! = 7 ⋅ 6 ⋅ 5 ! 2 ⋅ 1 ⋅ 5 ! = 21 возможность выбрать майки, а у Ани — C 7 5 возможностей.

Так как C 7 5 = C 7 7 − 5 = C 7 2 , то без вычислений понятно, что у обеих девочек одинаковое количество возможностей: \(21\).

Треугольную таблицу принято называть треугольником Паскаля (в честь французского математика \(17\) в.). Данный треугольник был известен уже во втором веке до нашей эры в древней Индии. В \(XII\) веке он появился в работах математиков Китая. В Европе в \(XVI\) веке его описал немецкий математик М. Штифель и затем Паскаль в \(XVII\) веке.

Треугольник Паскаля состоит из числовых строчек (см. рисунок). В первой строчке одно число, во второй — два, в третьей — три, и т. д. Первое и последнее число каждой строчки равно \(1\). Каждое из остальных чисел равно сумме двух расположенных над ним чисел предыдущей строки.

Каждый элемент в треугольнике Паскаля соответствует сочетанию, в котором нижний коэффициент равен номеру строки, а верхний коэффициент равен номеру числа в строке.

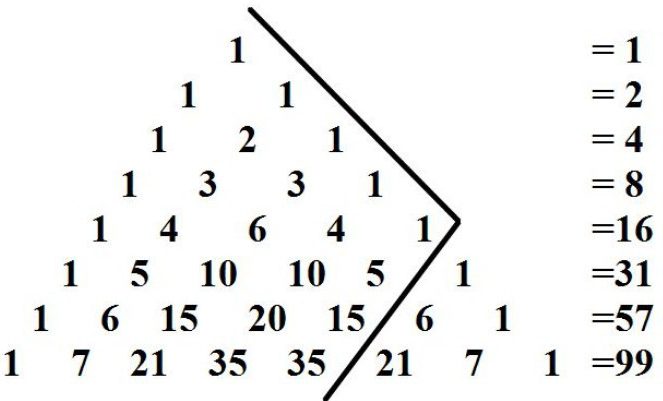
Используя треугольник Паскаля, можно сделать вывод, что, сложив числа в любой строчке треугольника Паскаля, можно получить степень числа \(2\).

Несколько слов о гении

Деятельность этого ученого с экстраординарным мышлением охватывает самые разные области науки. В частности, Блез Паскаль является одним из основателей гидростатики математического анализа, некоторых направлений геометрии и теории вероятностей. Кроме того, он:

создал механический калькулятор, известный под названием Паскалева колеса;
представил экспериментальное доказательство того, что воздух обладает упругостью и имеет вес;
установил, что барометр можно использовать для предсказания погоды;
изобрел тачку;
придумал омнибус — конные экипажи с фиксированными маршрутами, ставшие впоследствии первым видом регулярного общественного транспорта и пр.

Арифметический треугольник Паскаля

Немного истории

Справедливости ради нужно сказать, что на самом деле треугольник Паскаля был известен в Европе еще в начале 16 века. В частности, его изображение можно увидеть на обложке учебника арифметики известного астронома Петра Апиана из Ингольтштадского университета. Похожий треугольник представлен и в качестве иллюстрации в книге китайского математика Ян Хуэй, изданной в 1303 году. О его свойствах было известно также и замечательному персидскому поэту и философу Омару Хайяму еще в начале 12 века. Причем считается, что он познакомился с ним из трактатов арабских и индийских ученых, написанных ранее.

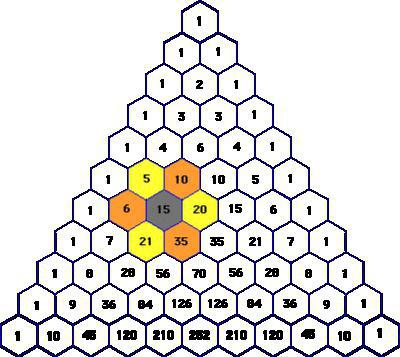
Описание

Прежде чем исследовать интереснейшие свойства треугольника Паскаля, прекрасного в своем совершенстве и простоте, стоит узнать, что он из себя представляет.

Говоря научным языком, эта числовая схема - бесконечная таблица треугольной формы, образованная из биномиальных коэффициентов, расположенных в определенном порядке. В его вершине и по бокам находятся цифры 1. Остальные позиции занимают числа, равные сумме двух чисел, расположенных над ними рядом выше. При этом все строки треугольника Паскаля симметричны относительно его вертикальной оси.

Основные свойства

Треугольник Паскаля поражает своим совершенством. Для любой строки под номером n (n = 0, 1, 2…) верно:

первое и последнее числа — 1;
второе и предпоследнее — n;
третье число равно треугольному числу (количеству кружков, которые можно расставить в виде равностороннего треугольника, т. е. 1, 3, 6, 10): T_n_-1 = n (n - 1) / 2.
четвертое число является тетраэдрическим, т. е. представляет собой пирамиду с треугольником в основании.

Кроме того, сравнительно недавно, в 1972 году, было установлено еще одно свойство треугольника Паскаля. Для того чтобы его обнаружить, нужно записать элементы этой схемы в виде таблицы со сдвигом строк на 2 позиции. Затем отмечают числа, делящиеся на номер строки. Оказывается, что номер столбца, в котором выделены все числа, является простым числом.

Тот же трюк можно осуществить и по-другому. Для этого в треугольнике Паскаля заменяют числа на остатки от их деления на номер строки в таблице. Затем располагают строки в полученном треугольнике так, чтобы следующая из них начиналась правее на 2 колонки от первого элемента предыдущей. Тогда столбцы, имеющие номера, являющиеся простыми числами, будут состоять только из нулей, а в тех, у которых они составные, будет присутствовать хотя бы один ноль.

Связь с биномом Ньютона

Как известно, так называется формула для разложения на слагаемые целой неотрицательной степени суммы двух переменных, которая имеет вид:

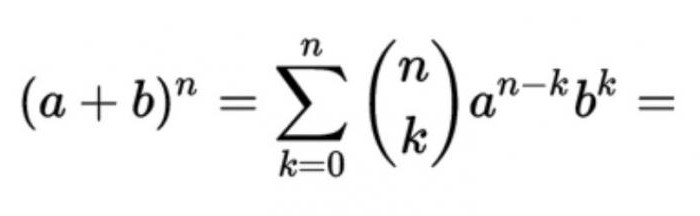
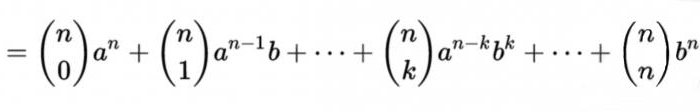
Присутствующие в них коэффициенты равны C_n m = n! / (m! (n - m)!), где m, представляет собой порядковый номер числа в строке n треугольника Паскаля. Иными словами, имея под рукой эту таблицу, можно легко возводить в степень любые числа, предварительно разложив их на два слагаемых.

Таким образом, треугольник Паскаля и бином Ньютона взаимосвязаны самым тесным образом.

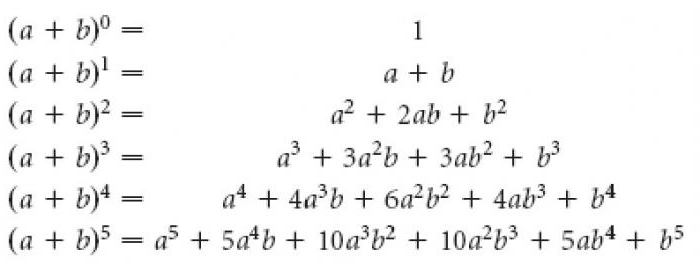
Математические чудеса

При внимательном изучении треугольника Паскаля можно обнаружить, что:

Треугольник Серпинского

Такая интересная математическая схема, достаточно перспективная с точки зрения решения сложных задач, получается, если раскрасить четные числа Паскалевого изображения в один цвет, а нечетные — в другой.

Треугольник Серпинского можно выстроить и другим образом:

в закрашенной схеме Паскаля перекрашивают в другой цвет серединный треугольник, который образован путем соединения середин сторон исходного;
точно также поступают с тремя незакрашенными, расположеными в углах;
если процедуру продолжать бесконечно, то в итоге должна получиться двухцветная фигура.

Самое интересное свойство треугольника Серпинского — его самоподобие, так как он состоит из 3-х своих копий, которые уменьшены в 2 раза. Оно позволяет отнести эту схему к фрактальным кривым, а они, как показывают новейшие исследования лучше всего подходят для математического моделирования облаков, растений, дельт рек, да и самой Вселенной.

Несколько интересных задач

Где используется треугольник Паскаля? Примеры задач, которые можно решать с его помощью, достаточно разнообразны и относятся к различным областям науки. Рассмотрим некоторые, наиболее интересные из них.

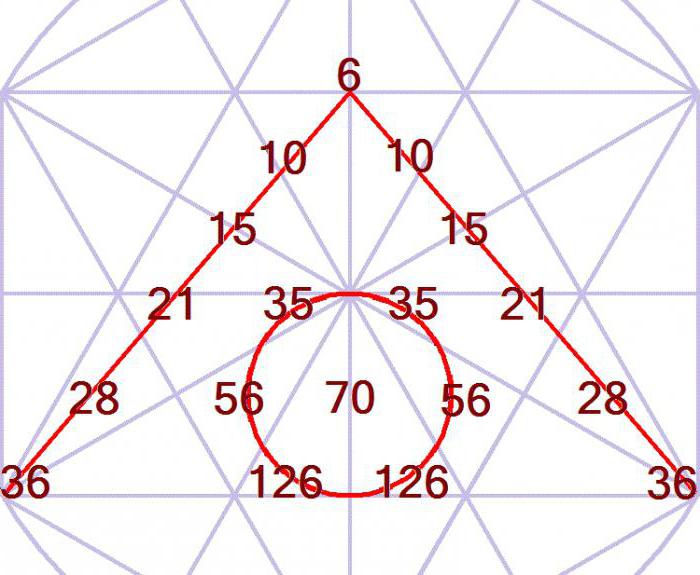
Задача 1. У некоторого большого города, обнесенного крепостной стеной, только одни входные ворота. На первом перекрестке основная дорога расходится на две. То же происходит и на любом другом. В город заходят 210 человек. На каждом из встречающихся перекрестков они делятся пополам. Сколько человек будет находить на каждом перекрестке, когда делиться будет уже невозможно. Ее ответом является 10 строка треугольника Паскаля (формула коэффициентов представлена выше), где по обе стороны от вертикальной оси расположены числа 210.

Задача 2. Имеется 7 наименований цветов. Нужно составить букет из 3 цветков. Требуется выяснить, сколькими различными способами это можно сделать. Эта задача из области комбинаторики. Для ее решения опять же используем треугольник Паскаля и получаем на 7 строке на третьей позиции (нумерация в обоих случаях с 0) число 35.

Теперь вы знаете, что изобрел великий французский философ и ученый Блез Паскаль. Его знаменитый треугольник при правильном использовании может стать настоящей палочкой-выручалочкой для решения множества задач, особенно из области комбинаторики. Кроме того, его возможно использовать для разгадывания многочисленных загадок, связанных с фракталами.

Читайте также: