Средняя гармоническая в статистике кратко
Обновлено: 04.07.2024
Если имеется n коэффициентов роста, то формула среднего коэффициента:
Средняя геометрическая равна корню степени n из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего. Средняя квадратическая простая определяется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число:
Средняя квадратическая взвешенная:
2. Выделяют следующие основные виды средних величин:
☞ по наличию признака-веса: невзвешенная и взвешенная;
☞ охвату совокупности: групповая, общая;
☞ форме расчета: средняя арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т. д. величины.
Данные средние выводятся из формулы степенной средней:
где xi – величины, для которых исчисляется средняя;
– средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;
n – частота (повторяемость индивидуальных значений признака).
При при k = – средняя гармоническая; при k = 0 – средняя геометрическая; при k = 2 – средняя квадратическая.
При k = 1 формула расчета степенной средней превращается в формулу расчета средней арифметической:
3. Выделяют следующие основные виды средней арифметической величины: средняя арифметическая невзвешенная, средняя арифметическая взвешенная.
Средняя арифметическая невзвешенная величина наиболее распространена; рассчитывается путем деления значений признака каждого элемента совокупности на число элементов совокупности:
Средняя арифметическая взвешенная величина рассчитывается, если имеются сведения о количестве или доле единиц совокупности каждым значением осредняемого признака:
Выделяют следующие основные свойства средней арифметической величины:
☞ сумма всех отклонений каждого значения признака от среднего арифметического значения равна нулю:
Если отклонения каждого из вариантов от средней величины суммировать, то получится ноль, что свойственно арифметическим невзвешенным и взвешенным средним значениям;
☞ произведение каждого значения признака на соответствующую ему частоту равно произведению средней величины на сумму частот:
Средняя величина есть результат распределения объема совокупности поровну между всеми ее элементами;
☞ сумма квадратов отклонения индивидуальных значений признака от средней арифметической меньше суммы квадратов отклонения от любой другой величины:
если увеличить или уменьшить все варианты осредняемого признака на какое-либо одно и то же число, то объем средней соответственно увеличится или уменьшится на это же число;
☞ если увеличить или уменьшить все варианты осредняемого признака в какое-либо число раз, то объем средней соответственно увеличится или уменьшится в это же количество раз;
☞ от увеличения или уменьшения веса каждого варианта признака в какое-либо число раз величина средней не изменится. Применение данного свойства удобно, если необходимо проанализировать совокупность со значительным количеством элементов, а частота элементов выражена многозначными числами. Если частоты элементов равны между собой, то среднюю можно рассчитать как невзвешенную;
☞ вследствие предыдущего свойства величина средней зависит не от абсолютных значений весов отдельных элементов, а от их доли в общей сумме весов, т. е. если не известны абсолютные выражения весов элементов, а известны пропорции между ними, то они могут использоваться для расчета средней;
☞ средняя арифметическая совокупности, состоящей из постоянных величин, равна этой постоянной:
4. Приведем также формулы расчета средней гармонической, средней геометрической, средней квадратической и средней степенной величин.
Формула расчета степенной средней:
где xi – величины, для которых исчисляется средняя;
– средняя, где имеет место осреднение индивидуальных значений;
n – частота (повторяемость индивидуальных значений признака).
При к = формула превращается в формулу расчета средней гармонической.
Средняя гармоническая простая (невзвешенная) величина взаимосвязана со средней арифметической невзвешенной как величина, обратная средней арифметической, рассчитанная из обратных значений признака:
Средняя гармоническая взвешенная величина:
где ω – значения сводного, объемного, выступающего как признак-вес показателя.
Рассчитывается, когда имеются данные об объеме определяющего показателя, т. е. произведения осредняемого признака и признака-веса.
Также рассчитывается при наличии сведений об индивидуальных значениях осредняемого признака при отсутствии отдельных значений признака-веса.
Средняя степенная при показателе степени к = 0 становится средней геометрической величиной.
5. К основным видам средних геометрических величин относятся средняя геометрическая невзвешенная и средняя геометрическая взвешенная величины. Расчет средней геометрической невзвешенной величины: если показатель степени k = 0, то формула средней степенной
где П(хi) – произведение индивидуальных значений осредняемого признака.
Применяется при наличии n коэффициентов роста. Индивидуальные значения признаков при этом становятся относительными величинами динамики (построены в виде цепных величин как отношение к предыдущему уровню каждого уровня в ряду динамики).
Средняя геометрическая невзвешенная величина характеризует средний коэффициент роста.
Средняя геометрическая взвешенная применяется в случае, если темпы роста остаются неизменными в течение нескольких периодов:
где – средняя геометрическая взвешенная (средний темп прироста);
х – количество периодов, при которых темпы роста оставались неизменными.
6. Средняя квадратическая – средняя степенная при показателе степени k = 2.
Различают следующие основные виды средних квадратических величин: средняя квадратическая невзвешенная, средняя квадратическая взвешенная.
Средняя квадратическая невзвешенная
используется при расчете степени колеблемости индивидуальных значений признака вокруг средней арифметической. Средняя квадратическая взвешенная:
Все формы средней (средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая и т. д.) образованы от единой степенной средней и отличаются друг от друга показателями степени k.
Правильность расчета средней величины можно проверить с помощью правила мажорантности: чем выше степень рассчитываемой формы средней величины, тем больше значение средней:
Рассмотрим среднее гармоническое, - меру центральной тенденции, использующуюся для усреднения обратных значений, - в рамках изучения количественных методов по программе CFA.
Среднее арифметическое, взвешенное среднее и среднее геометрическое являются наиболее часто используемыми концепциями среднего в инвестициях. Четвертая концепция - среднее гармоническое \( \overline X_H \), подходит для ограниченного числа применений.
Формула среднего гармонического.
Среднее гармоническое (англ. 'harmonic mean') множества наблюдений \( X_1, X_2, \ldots, X_n \) есть
\(\large \dst
\overline X_H = n \Big/ \sum_^(1/X_i) \) (Формула 7)
где \(X_i > 0\) для \(i = 1,2, . n\)
Среднее гармоническое значение - это значение, полученное путем суммирования обратных значений наблюдений - членов вида \( 1 / X_i \); - затем выполняется усреднение этой суммы путем деления ее на число наблюдений \( n \) и, наконец, нахождение обратной величины среднего.
Среднее гармоническое можно рассматривать как особый тип взвешенного среднего, в котором вес наблюдения обратно пропорционален его величине.
Концепцию лучше всего объяснить с помощью иллюстрации.
Пример расчета и пременения среднего гармонического.
Хорошо известный пример применения среднего гармонического возникает в инвестиционной стратегии, известной как усреднение издержек (англ. 'cost averaging'), которая включает периодическое инвестирование фиксированной суммы денег.
В этом случае усредненные коэффициенты - это цены на акцию на дату покупки, и мы применяем эти цены к постоянной фиксированной сумме, чтобы получить переменное количество акций.
Предположим, что инвестор покупает €1,000 ценных бумаг каждый месяц в течение \(n = 2\) месяцев. Цены на акции составляют €10 и €15 на две даты покупки.
Какова средняя цена акций?
В этом примере в 1-м месяце мы приобретаем €1,000 / €10 = 100 акций, а во 2-м месяце мы приобретаем €1,000 / €15 = 66.67 или 166.67 акций. Разделив общую сумму вложенных евро, €2,000, на общее количество приобретенных акций 166.67, мы получаем среднюю цену, уплаченную за акции, в размере €2,000 / 166.67 = €12.
Средняя цена фактически является средним гармоническим значением цен актива на даты покупки. По Формуле 7 средняя гармоническая цена составляет:
Значение €12 меньше среднеарифметической цены покупки акций:
Тем не менее, мы могли бы найти правильное значение €12, используя формулу средневзвешенного значения, где весовые коэффициенты, применяемые к ценам, равны долям акций, приобретенным по данной цене, от общего количества приобретенных акций.
В нашем примере расчет будет таким:
\( (100/166.67)\€10.00 + (66.67/166.67)\€15.00 = \€12 \)
Если бы мы инвестировали разные суммы денег на каждую дату, мы не могли бы использовать формулу гармонического среднего. Мы могли бы, однако, все еще использовать формулу взвешенного среднего значения способом, подобным только что описанному.
Математический факт, касающийся гармонического, геометрического и арифметического среднего, заключается в том, что, если все наблюдения в наборе данных неодинаковы, среднее гармоническое значение меньше среднего геометрического, которое, в свою очередь, меньше среднего арифметического.
В приведенной иллюстрации средняя гармоническая цена действительно была меньше средней арифметической цены.
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности, ведь значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть и случайные.
Приведем примеры экономических показателей, основанных на вычислении средней величины и раскрывающих ее сущность:
- расчет средней заработной платы работников предприятия осуществляется делением общего фонда заработной платы на число работников;
- средний размер вклада в банке находят делением суммы вкладов в денежном выражении на количество вкладов;
- для определения средней дневной выработки одного работника необходимо объем работ (количество деталей), выполненных работником за определенный период разделить на число дней в этом периоде.
Виды средних величин, используемых в статистике
Рассмотрим основные виды средних величин, используемых при решении социально-эконмических и аналитических задач.
Средняя арифметическая простая вычисляется по формуле:
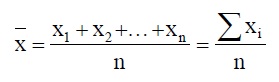 |
Средняя арифметическая простая используется в тех случаях, когда расчет осуществляется по не сгруппированным данным. Пример применения формулы средней арифметической простой представлен в задаче 1.
Средняя арифметическая взвешенная определяется по формуле:
При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам. Пример применения формулы средней арифметической взвешенной представлен в задаче 2.
Средняя гармоническая простая определяется по формуле:
Средние гармонические используются тогда, когда по экономическому содержанию имеется информация для числителя, а для знаменателя ее необходимо предварительно определить.
Средняя гармоническая взвешенная определяется по формуле:
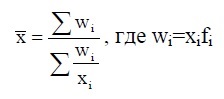 |
Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов. Пример применения формулы средней гармонической взвешенной представлен в задаче 3.
Средняя геометрическая простая (невзвешенная) опеределяется по формуле:
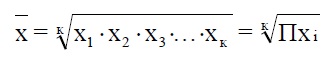 |
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.
Средняя квадратическая простая (невзвешенная) опеределяется по формуле:
Средняя квадратическая лежит в основе вычислений ряда сводных расчетных показателей.
Наиболее часто используемыми в экономической практике структурными средними являются мода и медиана. Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Медианой (Ме) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Пример определения медианы и моды для дискретного ряда чисел представлен в задаче 1.
Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.
Для интервального ряда расчет моды осуществляется по формуле:
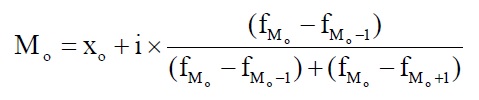 |
где Хо - нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); i - величина модального интервала; f Мо - частота модального интервала; f Мо-1 - частота интервала, предшествующего модальному; f Мо+1 - частота интервала, следующего за модальным.
Для интервального ряда расчет медианы осуществляется по формуле:
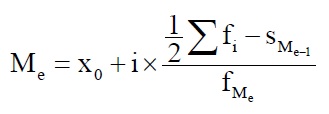 |
Хо - нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); i - величина медианного интервала; Sme-1 - накопленная частота интервала, предшествующего медианному; f Me - частота медианного интервала.
Задача 1. Дан ряд чисел: 15; 15; 12; 14; 13. Найдите размах, среднее арифметическое, медиану и моду этого ряда.
Решение
1) Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел. В данном случае размах равен R = 15-12 = 3
2) Среднее арифметическое данного ряда находим по формуле средней арифметической простой. Хср = (15+15+12+14+13)/5=13,8
3) Для определения медианы необходимо предложенный ряд упорядочить – расположить числа, например, в порядке возрастания: 12; 13; 14; 15; 15.
Медиана нечетного количества чисел в дискретном ряде – это число, записанное посередине. Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.
Поскольку в нашем случае количество чисел ряда нечетноне, то Ме = 14.
4) Мода дискретного ряда чисел – это число, которое встречается в данном ряде чаще других. Так как число 15 встречается в нашем ряде чаще других, то Мо = 15.
Задача 2. Имеется информация о численности студентов ВУЗов города и удельном весе (%) обучающихся студентов на коммерческой основе:
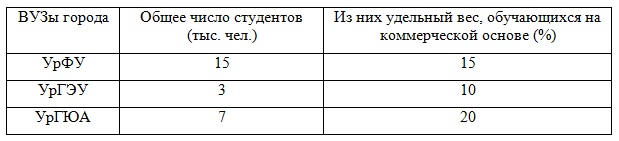 |
Определить: 1) средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе; 2) число этих студентов.
Решение
Для решения расширим предложенную таблицу:
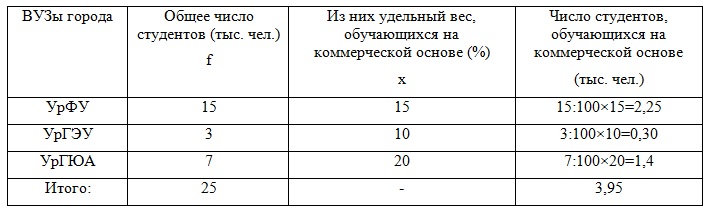 |
Ответ. Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе равен 15,8%, число этих студентов – 3 950 человек.
Задача 3. Сумма невыплаченной своевременно задолженности по кредитам на 1 июля составила 92,4 млн. денежных единиц. По отдельным отраслям экономики она распределялась следующим образом:
 |
Определить средний процент невыплаченной своевременно задолженности. Обоснуйте выбор формы средней.
Решение
Поскольку на различных предприятиях сумма задолженности по кредитам разная при разных удельных весах, то применим формулу средней гармонической взвешенной.
Хср = ΣW / Σ(W/х) = (32+14+46,4)/(32/20+14/28+46,4/16) = 92,4/5 = 18,48 %.
Ответ. Средний процент невыплаченной своевременно задолженности равен 18,48%.
Другие статьи по данной теме:
Список использованных источников
2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности, ведь значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть и случайные.
Приведем примеры экономических показателей, основанных на вычислении средней величины и раскрывающих ее сущность:
- расчет средней заработной платы работников предприятия осуществляется делением общего фонда заработной платы на число работников;
- средний размер вклада в банке находят делением суммы вкладов в денежном выражении на количество вкладов;
- для определения средней дневной выработки одного работника необходимо объем работ (количество деталей), выполненных работником за определенный период разделить на число дней в этом периоде.
Виды средних величин, используемых в статистике
Рассмотрим основные виды средних величин, используемых при решении социально-эконмических и аналитических задач.
Средняя арифметическая простая вычисляется по формуле:
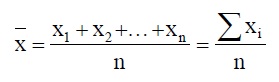 |
Средняя арифметическая простая используется в тех случаях, когда расчет осуществляется по не сгруппированным данным. Пример применения формулы средней арифметической простой представлен в задаче 1.
Средняя арифметическая взвешенная определяется по формуле:
При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам. Пример применения формулы средней арифметической взвешенной представлен в задаче 2.
Средняя гармоническая простая определяется по формуле:
Средние гармонические используются тогда, когда по экономическому содержанию имеется информация для числителя, а для знаменателя ее необходимо предварительно определить.
Средняя гармоническая взвешенная определяется по формуле:
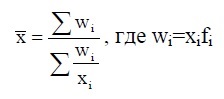 |
Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов. Пример применения формулы средней гармонической взвешенной представлен в задаче 3.
Средняя геометрическая простая (невзвешенная) опеределяется по формуле:
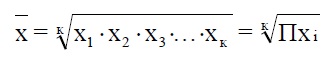 |
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.
Средняя квадратическая простая (невзвешенная) опеределяется по формуле:
Средняя квадратическая лежит в основе вычислений ряда сводных расчетных показателей.
Наиболее часто используемыми в экономической практике структурными средними являются мода и медиана. Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Медианой (Ме) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Пример определения медианы и моды для дискретного ряда чисел представлен в задаче 1.
Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.
Для интервального ряда расчет моды осуществляется по формуле:
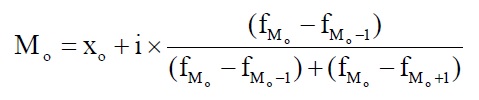 |
где Хо - нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); i - величина модального интервала; f Мо - частота модального интервала; f Мо-1 - частота интервала, предшествующего модальному; f Мо+1 - частота интервала, следующего за модальным.
Для интервального ряда расчет медианы осуществляется по формуле:
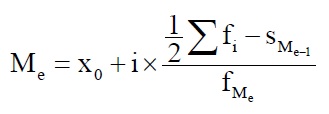 |
Хо - нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); i - величина медианного интервала; Sme-1 - накопленная частота интервала, предшествующего медианному; f Me - частота медианного интервала.
Задача 1. Дан ряд чисел: 15; 15; 12; 14; 13. Найдите размах, среднее арифметическое, медиану и моду этого ряда.
Решение
1) Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел. В данном случае размах равен R = 15-12 = 3
2) Среднее арифметическое данного ряда находим по формуле средней арифметической простой. Хср = (15+15+12+14+13)/5=13,8
3) Для определения медианы необходимо предложенный ряд упорядочить – расположить числа, например, в порядке возрастания: 12; 13; 14; 15; 15.
Медиана нечетного количества чисел в дискретном ряде – это число, записанное посередине. Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.
Поскольку в нашем случае количество чисел ряда нечетноне, то Ме = 14.
4) Мода дискретного ряда чисел – это число, которое встречается в данном ряде чаще других. Так как число 15 встречается в нашем ряде чаще других, то Мо = 15.
Задача 2. Имеется информация о численности студентов ВУЗов города и удельном весе (%) обучающихся студентов на коммерческой основе:
 |
Определить: 1) средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе; 2) число этих студентов.
Решение
Для решения расширим предложенную таблицу:
 |
Ответ. Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе равен 15,8%, число этих студентов – 3 950 человек.
Задача 3. Сумма невыплаченной своевременно задолженности по кредитам на 1 июля составила 92,4 млн. денежных единиц. По отдельным отраслям экономики она распределялась следующим образом:
 |
Определить средний процент невыплаченной своевременно задолженности. Обоснуйте выбор формы средней.
Решение
Поскольку на различных предприятиях сумма задолженности по кредитам разная при разных удельных весах, то применим формулу средней гармонической взвешенной.
Хср = ΣW / Σ(W/х) = (32+14+46,4)/(32/20+14/28+46,4/16) = 92,4/5 = 18,48 %.
Ответ. Средний процент невыплаченной своевременно задолженности равен 18,48%.
Другие статьи по данной теме:
Список использованных источников
2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна
Читайте также:

