Соотношение между сторонами и углами прямоугольного треугольника кратко

Обновлено: 30.06.2024

Сумма углов треугольника равна 180 ° , а прямой угол равен 90 ° , поэтому сумма двух острых углов прямоугольного треугольника ∡ $1$ $+$ ∡ $2 =$ 90 ° .

Катет прямоугольного треугольника, лежащий против угла в 30 ° , равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в  30 ° ).

Рассмотрим прямоугольный треугольник $ABC$, в котором ∡ $A$ — прямой, ∡ $B =$ 30 ° , и значит, что ∡ $C =$ 60 ° .

Докажем, что $BC = 2 AC$.
Приложим к треугольнику $ABC$ равный ему треугольник $ABD$, как показано на рисунке.

Получим треугольник $BCD$, в котором ∡ $B =$ ∡ $D =$ 60 ° , поэтому $DC = BC$. Но $DC = 2 AC$. Следовательно, $BC = 2 AC$.

Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30 ° .

Основываясь на общих признаках равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства, потому что в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны.

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.

2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.

3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

Будем рассматривать прямоугольный треугольник $ABC$ c прямым углом $C$ (рис. 1).

Рисунок 1. Прямоугольный треугольник

Будем рассматривать угол $A$. Тогда катет $BC$ будет называться противолежащим катетом, а катет $AC$ прилежащим к углу $A$.

Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника

Введем определения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе данного треугольника.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе данного треугольника.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету данного треугольника.

Синусом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету данного треугольника.

Из формул (1) и (2) очевидно, что

Проверим теперь следующее тождество:

Подставим формулы (1) и (2), получим

Тождество (5) называется основным тригонометрическим тождеством.

Готовые работы на аналогичную тему

Основные значения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника

Вычислим значения синуса, косинуса, тангенса и котангенса для $^^\circ >,\ ^^\circ >$ и $^^\circ >$. Для этого вспомним следующую теорему.

Катет прямоугольного треугольника, лежащий напротив угла в $^^\circ >$, равняется половине гипотенузы этого треугольника.

Пусть для начала у нас $\angle A=^^\circ >$. Так как треугольник прямоугольный, то $\angle B=^^\circ >$.

По теореме 1, имеем $AB=2BC$.

Используя основное тригонометрическое тождество (5), получим:

Теперь нетрудно найти тангенсы и котангенсы этих углов.

Пусть теперь $\angle A=^^\circ >$. Тогда $\angle B=^^\circ >$, то есть прямоугольный треугольник -- равнобедренный. По теореме Пифагора $^2+^2=^2$, следовательно, $^2=^2=2^2$, то есть

Сведем все полученные данные в таблицу (таблица 1).

Рисунок 2. Основные значения синусов, косинусов, тангенсов и котангенсов

Пример задачи на нахождение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника.

Найти значение синуса, косинуса, тангенса и котангенса угла $A$, если $AB=5,\ BC=4,\ AC=3.$

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Свойство. Сумма двух острых углов прямоугольного треугольника равна 90 0

Свойство. Катет прямоугольного треугольника, лежащий против угла в 30 0 , равен половине гипотенузы.

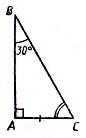
Признаки равенства:

Теорема. Два прямоугольных треугольника равны, если катеты одного равны катетам другого.

Теорема. Два прямоугольных треугольника равны, если гипотенуза и катет одного равны гипотенузе и катету другого.

Теорема. Два прямоугольных треугольника равны, если острый угол и сторона одного равны острому углу и стороне другого.

Теорема Пифагора

Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

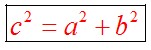
Теорема, обратная теореме Пифагора. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

Соотношение углов и сторон прямоугольного треугольника

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

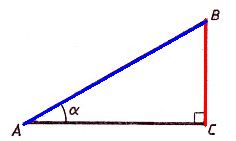
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

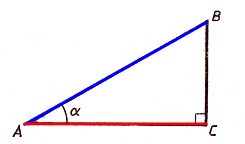
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Важные значения! ИХ ОБЯЗАТЕЛЬНО ЗАПОМНИТЬ!

Высота прямоугольного треугольника, проведенного из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.

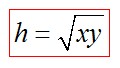
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины прямого угла.

Читайте также: