Случайные величины кратко и понятно
Обновлено: 05.07.2024
Случайная величина как фундаментальное понятие теории вероятности имеет большое значение в ее приложениях. Это понятие является абстрактным выражением случайного события. Более того, оперировать со случайными величинами иногда более удобно, чем со случайными событиями.
Случайной называется величина, которая в результате опыта может принять то или иное (но только одно) значение (до опыта неизвестно, какое именно).
События принято обозначать большими буквами латинского алфавита, вероятность буквой Р, например, Р(А). Реализации события (случайные величины) обозначаются малыми буквами: a1, a2, …, an.
Поскольку в теории вероятностей и математической статистике рассматриваются массовые явления, то случайная величина, как правило, характеризуется возможными значениями и их вероятностями.
Среди встречающихся в практике случайных величин можно выделить дискретные и непрерывные.
Дискретными случайными величинами называются такие, которые принимают только отделенные друг от друга значения и могут быть заранее перечислены. Например, количество автомобилей на заданном километровом участке дороги в конкретный момент времени; число бракованных узлов деталей автомобиля в партии из n штук.
Для дискретных случайных величин характерно, что они принимают отдельные, изолированные значения, которые можно заранее перечислить. Например, количество автомобилей на заданном участке дороги может принимать только целочисленные значения 0, 1,2, . п и зависит от времени суток и интенсивности движения.
Существуют случайные величины другого типа, которые чаще встречаются и имеют большое практическое значение.
Непрерывной случайной величиной называется такая, возможные значения которой непрерывно заполняют некоторый промежуток (интервал числовой оси). Интервал числовой оси может быть конечным или бесконечным. Примерами непрерывных случайных величин являются время безотказной работы автомобиля в заданных дорожных условиях, скорость движения автомобиля на заданной дороге, ошибка измерения.
В отличие от дискретных возможные значения непрерывных случайных величин нельзя заранее перечислить, так как они непрерывно заполняют некоторый промежуток.
Случайные величины обозначаются обычно большими буквами латинского алфавита - X, Y, Z, Т, а их возможные значения соответствующими малыми xi, yi, zi, ti, где i = 1, 2, . п.
Рассмотрим дискретную случайную величину X с возможными значениями x1, x2, …, xn. В результате проведения многократных опытов величина Т может принять каждое из значений xi, т. е.:
Обозначим вероятности этих событий буквой р с соответствующими индексами:
Последнюю формулу следует читать так: вероятность того, что случайная величина Т примет конкретное значение x1, равна p1 и т.д.
Исходя из того, что события xi образуют полную группу несовместимых событий, т. е. никаких других событий произойти не может, сумма вероятностей всех возможных значений случайной величины Т равна единице.
Эта суммарная вероятность каким-то образом распределена между отдельными значениями случайной величины
Дискретную случайную величину можно полностью описать с вероятностной точки зрения, если точно указать вероятность каждого события, т. е. задать это распределение. Этим будет установлен закон распределения случайной величины.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Зная его, можно до опыта судить о том, какие значения случайной величины будут появляться чаще и какие реже. Способы или формы представления закона распределения случайной величины различны.
Простейшей формой задания закона распределения дискретной случайной величины Т является ряд распределения или таблица, в которой перечислены возможные значения этой величины и соответствующие им вероятности:
| xi | x1 | x2 | … | xn |
| pi | p1 | p | … | pn |
Чтобы придать ряду распределения дискретных случайных величин более наглядный вид, его часто изображают графически.
При графическом представлении все возможные значения случайной величины откладывают по оси абсцисс, а соответствующие вероятности - по оси ординат.

Вершины полученных ординат обычно соединяют прямыми или пунктирными линиями. Это особенно целесообразно, если на одном графике представлено несколько кривых распределений. Соединяют вершины только для наглядности, так как в промежутках между соседними значениями случайная величина X значений принять не может, так как она дискретная, а ее вероятность в этих промежутках равна нулю. Такая фигура, изображенная на рис. 2.1, называется многоугольником распределения.
| Рис. 2.1. Многоугольник распределения дискретной случайной величины |
Многоугольники распределения могут принимать различные формы. Однако все они обладают общим свойством: сумма ординат многоугольника распределения, представляющая сумму вероятностей всех возможных значений случайной величины, всегда равна единице. Следует особо разграничить деление случайных величин на дискретные и непрерывные. Так, ряд распределения является удобной формой представления закона распределения для дискретной случайной величины, характеризуемой конечным числом возможных значений. Однако для непрерывной случайной величины ряд распределения вообще нельзя построить, поскольку она характеризуется бесчисленным множеством возможных значений, которые сплошь заполняют некоторый промежуток, и перечислить их в таблице трудно.
Различные диапазоны возможных значений случайной величины все же являются неодинаково вероятными, и для непрерывной величины существует распределение величин интервалов, а не конкретных значений.
Для количественной оценки этого распределения вероятностей используется не вероятность события X = x, а вероятность события X
Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:
Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.
Случайные величины, как правило, обозначают через *, а их значения – соответствующими маленькими буквами с подстрочными индексами, например, .
* Иногда используют , а также греческие буквы
Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:
– количество очков, которое выпадет после броска игрального кубика.
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина может принять одно из следующий значений:
– количество мальчиков среди 10 новорождённых.
Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:
, либо мальчиков – один и только один из перечисленных вариантов.
И, дабы соблюсти форму, немного физкультуры:
– дальность прыжка в длину (в некоторых единицах).
Её не в состоянии предугадать даже мастер спорта :)
Тем не менее, ваши гипотезы?
Коль скоро речь идёт о множестве действительных чисел, то случайная величина может принять несчётно много значений из некоторого числового промежутка. И в этом состоит её принципиальное отличие от предыдущих примеров.
Таким образом, случайные величины целесообразно разделить на 2 большие группы:
1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.
…нарисовались непонятные термины? Срочно повторяем основы алгебры!
2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.
Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ
Сначала разберём дискретную случайную величину, затем – непрерывную.
Закон распределения дискретной случайной величины
А теперь очень важный момент: поскольку случайная величина обязательно примет одно из значений , то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице:
или, если записать свёрнуто:
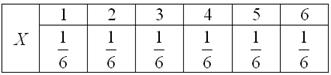
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:
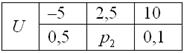
Некоторая игра имеет следующий закон распределения выигрыша:
…наверное, вы давно мечтали о таких задачах :) Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.
Решение: так как случайная величина может принять только одно из трёх значений, то соответствующие события образуют полную группу, а значит, сумма их вероятностей равна единице:
– таким образом, вероятность выигрыша условных единиц составляет 0,4.
Контроль: , в чём и требовалось убедиться.
Ответ:
Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины – размера выигрыша, если из коробки наугад извлекается один билет.
Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно рублей.
Всего таковых билетов 50 – 12 = 38, и по классическому определению:
– вероятность того, что наудачу извлечённый билет окажется безвыигрышным.
С остальными случаями всё просто. Вероятность выигрыша рублей составляет:
Проверка: – и это особенно приятный момент таких заданий!
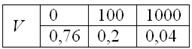
Ответ: искомый закон распределения выигрыша:
Следующее задание для самостоятельного решения:
Вероятность того, что стрелок поразит мишень, равна . Составить закон распределения случайной величины – количества попаданий после 2 выстрелов.
…я знал, что вы по нему соскучились :) Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.
Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.
Математическое ожидание дискретной случайной величины
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина принимает значения с вероятностями соответственно. Тогда математическое ожидание данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:
или в свёрнутом виде:
Вычислим, например, математическое ожидание случайной величины – количества выпавших на игральном кубике очков:
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.
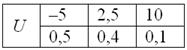
Теперь вспомним нашу гипотетическую игру:
, таким образом, математическое ожидание данной игры проигрышно.
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры :) Ну, может, только ради развлечения.
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.
Но прежде будет полезно размять пальцы на клавишах калькулятора:
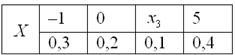
Случайная величина задана своим законом распределения вероятностей:
Найти , если известно, что . Выполнить проверку.
Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.
Решения и ответы:
Пример 3. Решение: по условию – вероятность попадания в мишень. Тогда:
– вероятность промаха.
Составим – закон распределения попаданий при двух выстрелах:
– два попадания. По теореме умножения вероятностей независимых событий:
Проверка: 0,09 + 0,42 + 0,49 = 1
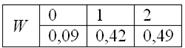
Ответ:
Примечание: можно было использовать обозначения – это не принципиально.
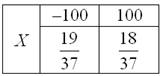
Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид:
Вычислим математическое ожидание:
Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.
Пример 5. Решение: по определению математического ожидания:
поменяем части местами и проведём упрощения:
таким образом:
Выполним проверку:
, что и требовалось проверить.
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
1. Формирование представление о случайной величине, дискретных и непрерывных случайных величинах.
2. Знакомство с законом распределения дискретной случайной величины, функцией распределения и плотностью распределения непрерывной случайной величины, числовых характеристиках случайных величин.
1. Виды случайных величин.
2. Закон распределения дискретной случайной величины.
3. Функция распределения вероятностей случайной величины.
4. Плотность распределения вероятностей непрерывной случайной величины.
5. Математическое ожидание.
6. Дисперсия и среднеквадратическое отклонение.
1. Виды случайных величин.
Случайной величиной называется такая величина, которая случайно принимает какое-то значение из множества возможных значений.
Случайные величины обозначаются: X , Y , Z . Значения, которые они принимают: x , y , z .
По множеству возможных значений различают дискретные и непрерывные случайные величины.
Дискретными называются случайные величины, значениями которых являются только отдельные точки числовой оси. (Число их может быть как конечно, так и бесконечно).
Пример: Число родившихся девочек среди ста новорожденных за последний месяц- это дискретная случайная величина, которая может принимать значения 1,2,3,…
Непрерывными называются случайные величины, которые могут принимать все значения из некоторого числового промежутка.
Пример: Расстояние, которое пролетит снаряд при выстреле- это непрерывная случайная величина, значения которой принадлежат некоторому промежутку [а; в].
2. Закон распределения дискретной случайной величины.
Дискретную случайную величину Х можно характеризовать законом распределения .
Закон распределения дискретной случайной величины- это соответствие между возможными значениями случайной величины и их вероятностями.
Закон распределения можно задать таблично, аналитически, графически.
При задании закона распределения таблично, в первую строку таблицы вносятся возможные значения случайно величины, а во вторую- их вероятности.
Возможные значения данной случайной величины: 0, 1, 2, 3.
Тогда закон распределения данной дискретной случайной величины можно представить таблицей:
Для наглядности закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки с координатами (xi ; pi), а затем соединяют их отрезками прямых. Полученная фигура называется многоугольником распределения.
Однако, такой способ задания (перечисление всех возможных значений случайной величины и их вероятностей) не подходит для непрерывных случайных величин. Составить перечень их возможных значений невозможно.
3. Функция распределения вероятностей случайной величины.
Дадим новый способ задания любых типов случайных величин. С этой целью введем функцию распределения вероятностей случайной величины.
Функцией распределения случайной величины называют функцию F ( x ), определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньшее х, т.е. F ( x ) P ( X x ).
Геометрически это равенство можно истолковать так: F ( x ) –есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Свойства функции распределения:
Свойство 1: Значения функции распределения принадлежат интервалу [0; 1]: .
Свойство 2: F ( x )- неубывающая функция, т.е. при .
Следствие 1: Вероятность того, что случайная величина примет значение, заключенное в интервале (а; b ), равна приращению функции распределения на этом интервале:
Пример: Случайная величина Х задана функцией распределения:
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0; 2).
Следствие 2:
Свойство 3: Если возможные значения случайной величины принадлежат интервалу ( a ; b ), то F ( x )=0 при (т.к. ; F ( x )=1 при (т.к. - достоверное событие.
Следствие: Если возможные значения непрерывной случайной величины распределены на всей числовой оси, то справедливы следующие предельные соотношения:
Рассмотренные выше свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.
График расположен в полосе, ограниченной прямыми у=0, у=1 (1 свойство).
4. При возрастании значения х в интервале ( a ; b ), в котором заключены все возможные значения случайной величины, график растет вверх (2 свойство).
5. При ординаты графика равны 0, при ординаты графика равны 1 (3 свойство).
Замечание: График функции распределения дискретной случайной величины имеет ступенчатый вид.
Пример: Дискретная случайная величина Х задана таблицей распределения:
Найдите функцию распределения и постройте ее график.
Решение: Если , то F ( x )=0 по 3 свойству. Если , то F ( x )= P ( X Если , то F ( x )= P ( X Если х>8, то F ( x )=1. Действительно, событие Х
Итак, функция распределения имеет следующий вид:
4. Плотность распределения вероятностей непрерывной случайной величины.
Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (дифференциальной функцией).
Плотность распределения вероятностей непрерывной случайной величины Х называют функцию f ( x )- первую производную от функции распределения F ( x ).
Теорема: Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу ( a ; b ), равна определенному интегралу от плотности распределения, взятому в пределах от а до b .
Пример: Задана плотность вероятностей случайной величины Х.
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).
Свойства плотности распределения вероятностей:
Свойство 1: Плотность распределения- неотрицательная функция: f ( x ) > 0.
Свойство 2: Несобственный интеграл от плотности распределения в пределах от равен 1: .
Геометрический смысл этого свойства заключается в следующем: площадь криволинейной трапеции, ограниченной осью ОХ и кривой распределения, равна 1. В частности, если все возможные значения случайной величины принадлежат интервалу ( a ; b ), то .
Часто, для того чтобы характеризовать случайную величину используют числа, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины. К числу важнейших числовых характеристик относятся математическое ожидание и дисперсия.
5. Математическое ожидание.
Математическое ожидание приближенно равно среднему значению случайной величины. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и следовательно стреляет лучше.
Математическое ожидание дискретной случайной величины Х- это величина , где xi- значения случайной величины, pi- их вероятности, n - число возможных значений случайной величины.
Пример: Найдите математическое ожидание, зная закон распределения дискретной случайной величины.
Статистика занимается сбором, представлением (в виде таблиц, диаграмм, графиков и др.) и анализом информации о различных случайных величинах.
Случайными величинами (данными) называют такие величины, которые в ходе наблюдений или испытаний могут принимать различные значения. Можно говорить о том, что их значения зависят от случая.
Значения переменных, которые регистрируются с помощью чисел, имеющих содержательный смысл, называют количественными данными .
В зависимости от того, какие значения может потенциально принимать переменная, выделяют два типа количественных данных:
Если два варианта признака в данной совокупности могут отличаться один от другого не менее чем на определённое число или вообще совпадают, то такие данные называют дискретными .
Если случайная величина может принимать любое значение из некоторого промежутка, то такая величина называется непрерывной .
Процент учеников, которые имеют достаточный уровень подготовки по предмету в разных классах; время, за которое ученики пробежали \(60\) м на соревнованиях; продолжительность работы электронных ламп; температура воздуха, рост взрослого человека (например от \(140\) до \(230\) см) , фактическая масса буханки хлеба (например от \(750\) до \(830\) г) , дальность полёта снаряда, урожайность культуры, выращенной в хозяйстве и т. п.
Есть данные, которые регистрируют определённое качество, которым обладает объект. Такие данные называют качественными .
Качественные данные бывают двух типов: порядковые, для которых существует имеющий содержательный смысл порядок, и номинальные, для которых нет содержательно интерпретируемого порядка.

Для удобства обработки данных измерения используют представление информации в виде таблицы, гистограммы или полигона.
Гистограмма частот — это фигура, состоящая из прямоугольников, опирающихся на интервалы группировки.
Полигон частот представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.

Рассмотрены основные понятия темы: определение случайной величины, непрерывной СВ, дискретной СВ, дано понятие закона распределения ДСВ. Перечислены основные числовые харакеристки ДСВ. Приведены примеры. Даны контрольные задания.
Теоретический материал по теме
«Случайная величина. Понятия непрерывной и дискретной случайных величин. Закон распределения случайной величины,
Случайная величина. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Например, число бракованных лампочек среди 10 купленных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2,….,10. Случайные величины обозначаются прописными буквами латинского алфавита: X, Y, Zи так далее, а их значения – соответствующими строчными буквами x, y, zи так далее.
Случайная величина называется дискретной, если множество её значений конечно или счетно, то есть множество её значений представляет собой конечную последовательность x1, x2,….xn или бесконечную последовательность x1, x2. xn,…
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного множества. Число возможных значений непрерывной случайной величины бесконечно.
Законом распределения случайной величины называют соответствие между возможными значениями и их вероятностями. Его можно задавать таблично, аналитически и графически. Табличное задание закона:
,где x1,x2,…xn– возможности значения случайной величины Х;
p1,p2,…pn – вероятности случайной величины Х.
События X =x1, X =х2, . X=хn - полная система попарно несовместимых событий, поэтому сумма их вероятностей равна 1.
р 1+ р2 +. +рп = 1.
В издательстве выпущено 100 книг по овцеводству. Лотереей разыграны одна книга в 500 руб. и 10 по 10 руб. Найти закон распределения случайной величины х - возможного выигрыша одной книги.
Решение. Возможны значениях: Х1= 500, х2 = 10 ,х3 = 0. Вероятности: р1=0,01; р2 =0,1; р3=1 - (р1+ р2) = 0,89.
Функцией распределения случайной величины называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, то есть F(x) = P(Xx).
Кроме закона распределения, который дает полное представление о случайной величине, часто используют числа, которые описывают случайную величину суммарно. Такие числа называют числовыми характеристиками случайной величины. К ним относятся математическое ожидание, дисперсия и среднее квадратичное отклонение дискретной случайной величины.
Математическим ожиданием (М) дискретной величины называют сумму произведений всех ее возможных значений, умноженных на их вероятности.

,
где xi, - значение случайной величины, pi- вероятность случайной величины.
Часто требуется оценить рассеяние возможных значений случайной величины вокруг его среднего значения. Дисперсией (рассеянием) D(x) случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D(X) = М[Х-М(Х)] 2 .
Формула для вычисления дисперсии D(X) = М(Х 2 )-[М(Х)] 2 .
Свойства математического ожидания и дисперсии:
М(С) = С, c-const 1. D(C) = О, c-cоnst
М(СХ) = СМ(Х) 2. D(CX) = C 2 D(X), c-const
M(XV) = M(X) • M(V) 3. D(X+V) =D(X) + D(V)
4. M(X+M) = M(X) + M(V) 4. D(X-V) = D(X) + D(V)
Средним квадратичным отклонением ( (х)) случайной величины хназывают квадратный корень из дисперсии: ( х )
Исследование вариационных статистических рядов рассмотрим на примере.
Пример.: Дан дискретный вариационный ряд
где X x1x2, x3> характеристики случайной величины X,N n1, п2 ,п3> - частоты появления элементов в выборке.
Провести исследование дискретного вариационного ряда: 1) найти объём выборки, 2) составить закон распределения случайной величины X, 3) найти математическое ожидание, дисперсию и среднее квадратичное отклонение.
Решение. 1) Найдём объем выборки: п= n1+n2+п3=10+15+25=50.
2)Найдём относительные частоты: W1=10/50=1/5, w2=15/50=3/10, w3=25/50у =1/2.
Закон распределения случайной величины X представлен таблицей:
3) Найдём математическое ожидание, дисперсию и среднее квадратичное отклонение:
M=w1x1 + w2x2 + w3x3=l/5 • 1+3/10 ·4+1/2·6=4/4;
D= w1 (x1-M) 2 + w2 (x2 -M) 2 + w3 (x3 -M) 2 = 1/5 · (1-4,4) +3/10 · (4- 4,4) +1/2 · (6- 4,4)=3,64; (x) = = =1,9
Задания для самостоятельного выполнения
Задание 2. Решение упражнений по темам раздела:
а) На пути движения автомашины 4 светофора, каждый из которых запрещает дальнейшее движение автомашины с вероятностью 0,5. Найти ряд распределения числа светофоров, пройденных машиной до первой остановки. Чему равны математическое ожидание и дисперсия этой случайной величины?
б) Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Составить закон распределения числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7. Найти дисперсию этой случайной величины.
в) Стрелок, имея 3 патрона, стреляет в цель до первого попадания. Вероятности попадания при первом, втором и третьем выстрелах соответственно 0,6, 0,5, 0,4. С.В. ξξ - число оставшихся патронов. Составить ряд распределения случайной величины, найти математическое ожидание, дисперсию, среднее квадратичное отклонение с.в., построить функцию распределения с.в., найти P(|ξ−m|≤σP(|ξ−m|≤σ.
г) В ящике содержится 7 стандартных и 3 бракованных детали. Вынимают детали последовательно до появления стандартной, не возвращая их обратно. ξξ - число извлеченных бракованных деталей. Составить закон распределения дискретной случайной величины ξξ, вычислить ее математическое ожидание, дисперсию, среднее квадратическое отклонение, начертить многоугольник распределения и график функции распределения.
д) На переэкзаменовку по теории вероятностей явились 3 студента. Вероятность того, что первый сдаст экзамен, равна 0,8, второй - 0,7, третий - 0,9. Найдите ряд распределения случайной величины ξξ числа студентов, сдавших экзамен, постройте график функции распределения, найдите М(ξ),D(ξ).
е) Вероятность попадания в цель при одном выстреле равна 0,8 и уменьшается с каждым выстрелом на 0,1. Составить закон распределения числа попаданий в цель, если сделано три выстрела. Найти математическое ожидание, дисперсию и С.К.О. этой случайной величины. Построить график функции распределения.
ж) По цели производится 4 выстрела. Вероятность попадания при этом растет так: 0,2, 0,4, 0,6, 0,7. Найти закон распределения случайной величины XX - числа попаданий. Найти вероятность того, что X≥1X≥1.
Читайте также:

