Сложение и вычитание синусоидальных величин кратко

Обновлено: 30.06.2024

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, - периодом Т. Для периодического тока имеем

Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01 ¸ 10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i - мгновенное значение тока ;

u – мгновенное значение напряжения ;

е - мгновенное значение ЭДС ;

р - мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ) .

Действующее значение переменного тока

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е₁ и е₂ соответствуют уравнения:

Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени ( t =0): и - начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.

Для синусоидальных ЭДС е₁ и е₂ угол сдвига фаз:

Векторное изображение синусоидально
изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е₂ (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени ( t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:

Каждый из этих токов синусоидален и может быть представлен уравнением

Результирующий ток также будет синусоидален:

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы.

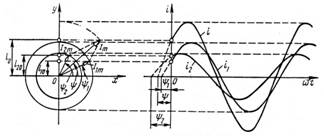
На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .

Представление синусоидальных ЭДС, напряжений
и токов комплексными числами

Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :

показательной

тригонометрической или

алгебраической - формах.

Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число

Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как

В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:

Комплексное число удобно представить в виде произведения двух комплексных чисел:

Параметр , соответствующий положению вектора для t =0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой: , а параметр - комплексом мгновенного значения.

Параметр является оператором поворота вектора на угол w t относительно начального положения вектора.

Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол ± a .

Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды и оператора поворота :

Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:

Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:

- то для записи ее в показательной форме, необходимо найти начальную фазу , т.е. угол, который образует вектор с положительной полуосью +1:

Тогда мгновенное значение напряжения:

При записи выражения для определенности было принято, что , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если , то при (второй квадрант)

а при (третий квадрант)

Если задано мгновенное значение тока в виде , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:

Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.

Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:

Действующее значение синусоидальных ЭДС, напряжений и токов

В соответствии с выражением (3) для действующего значения синусоидального тока запишем:

Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в раз:

Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения

1. Основы теории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?

2. Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?

3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?

4. Для заданных синусоидальных функций ЭДС и тока записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.

Для того, чтобы сложить две величины с помощью векторов, необходимо к концу первого вектора добавить второй, не изменяя его величины и направления. Соединив начало первого вектора с концом второго, получим суммарный вектор.

Рисунок 11. Векторная диаграмма напряжений для вариантаX_L=X_C,уголφ=0, U_L=U_C

Этот режим называется резонанс напряжений (U_L=U_C). Напряжения на элементах U_Lи U_C могут значительно превышать входное напряжение.

На векторной диаграмме рис. 9 или рис. 10 можно выделить треугольник, который принято называть треугольникомнапряжения.В этом треугольнике:

где ‑ активная составляющая напряжения;

— реактивная составляющая напряжения.

Поделив модули вектора треугольника напряжений на ток, получим подобный ему треугольник сопротивлений рис. 12.,

Рисунок 12. Треугольник сопротивлений

– активное сопротивление цепи;

- реактивное сопротивление цепи;

- полное сопротивление цепи.

Для варианта X_L=X_C, угол φ=0, U_L=U_C. Ток совпадает с напряжением. Цепь имеет активный характер. Полное сопротивление Z=R наименьшее из всех возможных значений X_L и X_C. Векторная диаграмма напряжений имеет вид (рис.11).

Резонанс напряжений- явление возрастания напряжений на реактивных элементах, превышающих напряжение на зажимах цепи при максимальном токе в цепи, которое совпадает по фазе с входным напряжением.

Условия возникновения резонанса:

Последовательное соединение L и C с генератором переменного тока;
Частота генератора должна быть равна частоте собственных колебаний контура , при этом характеристические сопротивления равны;
Сопротивление должно быть меньше, чем 2ρ, так как только в этом случае в цепи возникнут свободные колебания, поддерживаемые внешним источником.

Полное сопротивление цепи:

так как равны характеристические сопротивления. Следовательно, при резонансе цепь носит чисто активный характер, значит, входное напряжение, и ток в момент резонанса совпадают по фазе. Ток принимает максимальное значение.

При максимальном значении тока напряжения на участках L и C будут большими и равными между собой.

Напряжение на зажимах цепи:

Рассмотрим следующие соотношения:

Q – добротность контура –при резонансе напряжения показывает, во сколько раз напряжение на реактивных элементах больше входного напряжения генератора, питающего цепь. При резонансе коэффициент передачи последовательного колебательного контура

Если добротность равна 100, напряжение на зажимах 1В, то

Uc=Ul=QU=100В,

то есть напряжение на зажимах меньше напряжений на емкости и индуктивности. Это явление называется резонансом напряжений.

При резонансе, коэффициент передачи равен добротности.

Построим векторную диаграмму напряжения.

Напряжение на емкости равно напряжению на индуктивности, следовательно напряжение на сопротивлении равно напряжению на зажимах и совпадает по фазе с током.

В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.

Рисунок 4. Полное сопротивление цепи содержащей R, L и C.а) - схема цепи; б) - треугольник сопротивлений.

Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.

(4)

Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (X_L или X_C преобладает).

После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.

(5)

(6)

Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.

Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления

2.3. Последовательное соединение элементов с параметрамиR, L, С

Схема неразветвленной цепи синусоидального тока представлена на рис. 7. Энергетическое состояние цепи описывается для мгновенных значений уравнением:

, ,

Рисунок 7. Схема последовательного соединения элементов цепи

Если то напряжение на входных зажимах будет также изменяться по синусоидальному закону в силу линейности рассматриваемой цепи. После несложных преобразований дифференциальное уравнение цепи можно привести к виду:

Это уравнение позволяет построить временную диаграмму, которая полностью отражает амплитудные и фазовые соотношения в последовательной цепи. Для практических расчетов применяют векторные диаграммы,которые делают расчет цепи более наглядным и простым.

Под векторной диаграммой цепи понимают совокупность векторов ЭДС, напряжений и токов электрической цепи, построенных с соблюдением их взаимной ориентации по фазе. Так как чаще при анализе и расчете электрической цепи пользуются действующими значениями токов и напряжений, векторную диаграмму, как графическую интерпретацию расчета цепи, строят также для действующих значений напряжений и токов. При построении векторной диаграммы в качестве исходного вектора удобнее выбрать вектор величин, одинаковой для нескольких элементов цепи. В последовательной цепи (рис. 7) по всем участкам проходит один и тот же ток, поэтому за исходный вектор выбирается вектор тока и относительно его строятся под углом сдвига векторы напряжений на всех участках.

На топографической векторной диаграмме каждая точка соответствует определенной точке электрической цепи. Чтобы осуществить это соответствие точек диаграммы и цепи, построение векторов топографической диаграммы ведут в той же последовательности, в какой обходят электрическую цепь. На рис. 8 показана топографическая диаграмма для цепи рис. 7.

Рисунок 8. Векторная диаграмма токов и напряжений при последовательном соединении элементов цепи

5.3.1 Рекомендации для студента

В неразветвленной цепи протекает ток ;

Для неразветвленной цепи переменного тока с активным, емкостным и индуктивным сопротивлениями справедливы следующие соотношения:

· - напряжение на активном сопротивлении;

· - напряжение на индуктивности;

· - напряжение на емкости;

Преимущество изображения синусоидально изменяющихся величин векторами заключается в том, что при таком изображении сумма или разность нескольких величин может быть определена графически быстро и просто, в то время как при изображении величин синусоидами эти операции сложны и требуют много времени.

Допустим, необходимо сложить две ЭДС одной и той же частоты:

Мгновенное значение суммарной ЭДС равно алгебраической сумме мгновенных значений слагаемых величин: . Сложение двух синусоидальных величин можно выполнить графически путем сложения двух синусоид, изображающих эти величины (т.е. с помощью временных диаграмм). Для получения ординат суммарной кривой нужно для каждого момента времени сложить ординаты кривых, изображающих слагаемые величины. В результате получим синусоидальную кривую той же частоты. Из чертежа можно определить амплитуду и начальную фазу суммарной ЭДС. Чем больше слагаемых величин, тем труднее выполнить вышеописанную операцию.

Докажем, что вектор, изображающий эту синусоиду, равен геометрической сумме векторов, изображающих синусоиды слагаемых величин. Чтобы сложить две заданные ЭДС , представленные векторами и на рисунке 1.5, нужно вектор перенести параллельно самому себе так, чтобы его начало совпало с концом вектора (или вектор перенести параллельно самому себе, чтобы его начало совпало с концом вектора ). Тогда замыкающий вектор отобразит суммарную ЭДС.

Рисунок 1.5 – Сложение двух векторов

Действительно, при t=0 проекция вектора на ось ординат представляет собой мгновенное значение е₁, проекция вектора на ту же ось – мгновенное значение е₂, а сумма этих проекций (е₁+е₂) равна проекции на вертикальную ось суммарного вектора (е). При вращении векторов их взаимное расположение не изменяется, и для проекций по-прежнему выполняется равенство .

Таким образом, результатом сложения синусоидальных величин одинаковой частоты является синусоидальная величина той же частоты, амплитуда которой равна геометрической сумме амплитуд слагаемых синусоид.

При большом числе векторов их сложение производится тем же методом, т.е. векторы переносятся параллельно самим себе так, чтобы каждый последующий вектор начинался в конце предыдущего. Замыкающий вектор (соединяющий начало первого вектора с концом последнего) изображает суммарную величину.

Вычитание двух синусоидальных величин заменяют сложением уменьшаемой величины с вычитаемой, взятой с обратным знаком, т.е.

Следует помнить, что изменение знака у синусоидальной величины соответствует изменению начального фазового угла на 180 0 :

Если синусоидальные величины изображены векторами, то изменение знака означает поворот вектора на 180 0 .

При сложении двух синусоидальных величин различной частоты получается несинусоидальная величина, которая не может изображаться вращающимся вектором. Векторная диаграмма применима только для синусоидальных величин, имеющих одну и ту же частоту.

При сложении или вычитании синусоидальных величин одинаковой частоты получают синусоидальную величину той же частоты. Операции сложения или вычитания могут производится аналитически и графически – по временной и векторной диаграммам.
Наиболее удобный способ – графический по векторной диаграмме.
Алгебраическое сложение и вычитание векторов. Сложение векторов: один вектор остается на месте, другие переносятся параллельно самим себе так, чтобы начало последующего вектора совпадало с концом предыдущего. Вектор, проведенный из начала первого вектора в конец последнего, представляет суму всех векторов. Вычитание одного вектора из другого выполняется сложением прямого вектора с вычитаемым вектором, повернутым на 180°.

Цепь с активным сопротивлением

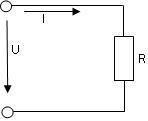
Мгновенное значение напряжения u=Um sin ωt
Так как цепь обладает только активным сопротивлением, то согласно закону Ома для участка цепи:

i=u/R= Um/R sin ωt = Im sin ωt – закон Ома для мгновенных значений.
Im = Um/R – закон Ома для амплитудных значений

Разделив обе части уравнения на √2, получим закон Ома для действующих значений

I = U/R

Ток и напряжение в цепи с активным сопротивлением совпадает по фазе.

Мгновенная мощность

Преобразуем формулу: sin 2 ωt=(1-cos2ωt)/2 и U_mI_m/2= U_mI_m/√2√2=UI,
в результате p=UI-UIcos 2 ωt.
Мгновенная мощность, оставаясь все время положительной, колеблется около уровня UI

Для определения расхода энергии за длительное время целесообразно пользоваться средним значением мощности.

P=UI

Цепь с индуктивностью

Под действием синусоидального напряжения в цепи с индуктивной катушкой без ферромагнитного сердечника проходит синусоидальный ток

i= Im sin ωt

В результате этого вокруг катушки возникает переменное магнитное поле и в катушке наводится ЭДС самоиндукции. При R=0 напряжение источника целиком идет на уравновешивание этой ЭДС.

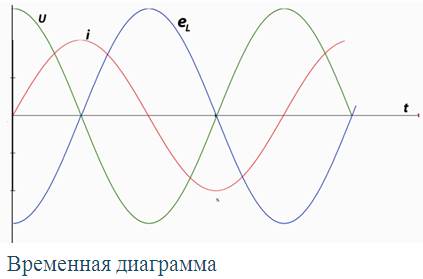Ток в цепи с индуктивностью отстает по фазе от напряжения на угол π/2. Это объясняется тем, что индуктивная катушка реализует инерцию электромагнитных процессов.

X_L – индуктивное сопротивление цепи
I_m=Um/X_L – закон Ома для амплитудных значений. Разделим на √2
I=U/X_L – закон Ома для действующих значений.

При одинаковых знаках напряжения и тока мощность положительна, а при разных знаках – отрицательна.
В среднем катушка не потребляет энергии, и, следовательно, активная мощность Р=0.

Реактивная мощность

Реактивная мощность
Для количественной характеристики интенсивности обмена энергией между источником и катушкой служит реактивная мощность.

Q=UI

Единицей реактивной мощности является вольт-ампер реактивный (ВАр)

Цепь с активным сопротивлением

i=u/R= Um/R sin ωt = Im sin ωt – закон Ома для мгновенных значений.
Im = Um/R – закон Ома для амплитудных значений

Разделив обе части уравнения на √2, получим закон Ома для действующих значений

I = U/R

Ток и напряжение в цепи с активным сопротивлением совпадает по фазе.

Мгновенная мощность

Для определения расхода энергии за длительное время целесообразно пользоваться средним значением мощности.

P=UI

Цепь с индуктивностью

i= Im sin ωt

Реактивная мощность

Q=UI

Единицей реактивной мощности является вольт-ампер реактивный (ВАр)

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Автор: Евгений Живоглядов.
Дата публикации: 20 марта 2015 .
Категория: Статьи.

Практика остановила свой выбор на синусоидальных колебаниях переменных электрических величин. В дальнейших статьях, говоря о токе, электродвижущей силе (ЭДС), напряжении и магнитном потоке, мы будем считать их изменяющимися по закону синуса.

Пусть мы имеем вектор 0А (рисунок 1), выражающий в масштабе какую либо переменную синусоидальную величину, например ток. Будем вращать с постоянной скоростью вектор вокруг точки 0 против часовой стрелки. Конец вектора буде описывать окружность, а угол, на который поворачивается вектор, будет меняться с течением времени.

Угловая скорость или угловая частота ω (омега) вращения равна углу поворота вектора в единицу времени. Формула угловой частоты:

Часто вместо градуса пользуются другой единицей измерения угла – радианом. Радианом называется угол, дуга которого равна радиусу. Если длина окружности C = 2 × π × R, то она содержит радиан.

За один оборот радиус-вектор 0A будет иметь один период вращения продолжительностью T секунд.
Угловая частота или угловая скорость вращения в этом случае выразится:

Так как , то ω = 2 × π × f (рад / сек.). Таким образом, мы знаем, как найти угловую скорость в зависимости от частоты f.

Угол поворота радиус-вектора α от начального положения будет равен:

Угол α называется фазным углом или фазой.

Проекция вектора 0А на вертикальный диаметр равна произведению величины вектора на синус фазного угла, то есть

Таким образом, проекция вращающегося вектора 0А на вертикальный диаметр изменяется по закону синуса. Если длина вектора будет A_m, то мгновенное значение величины проекции a равно:

В последнем случае мгновенное значение величины проекции равно ее амплитудному или максимальному значению.

Задаваясь величиной фазного угла и проектируя вектор A_m на вертикальный диаметр, будем получать мгновенное значение синусоидальной величины.

Проведем горизонтальную ось, на которой отложим фазные углы, проходимые вектором при его вращении (рисунок 2). Откладываем затем вертикальные отрезки, равные мгновенным значениям величины в местах окончания горизонтальных отрезков, соответствующих фазным углам. Соединяя концы вертикальных отрезков плавной кривой, получим знакомую нам кривую – синусоиду.

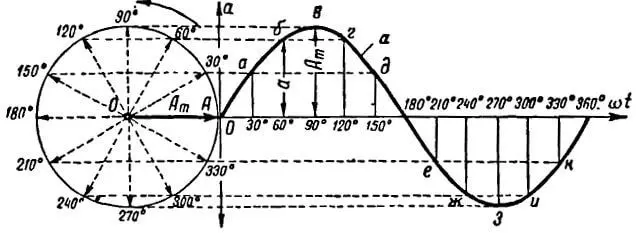
Рисунок 2. Получение синусоиды путем вращения векторов

Синусоидальная кривая получена в результате вращения вектора, который в масштабе выражал амплитудное (максимальное) значение переменной синусоидальной величины.

Способ изображения синусоидально меняющихся во времени величин с помощью векторов определенной длины и определенным образом расположенных между собой называется векторной диаграммой.

Та же зависимость может быть выражена графически в виде синусоидальных кривых.
Таким образом, переменную синусоидальную величину можно представить тремя способами: уравнением, векторной диаграммой и графиком.

Если радиус-вектор в начальный момент времени (t = 0) составляет некоторый угол ψ с горизонтальной осью, то в этом случае мгновенное значение переменной величины будет:

Угол ψ (пси) называется начальным фазным углом или начальной фазой.

Векторная диаграмма и график для этого случая даны на рисунке 3.

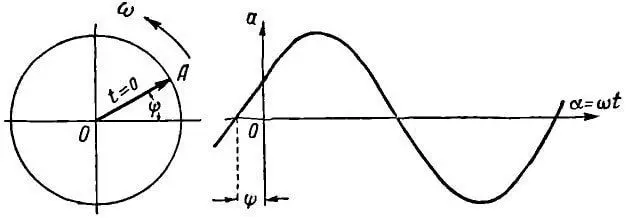
Рисунок 3. Построение синусоиды при наличии начальной фазы

Мы не внесем ничего нового, если будем вращать два вектора, совпадающие по направлению. В определенный момент времени оба вектора будут повернуты на один и тот же фазный угол. Поэтому как сами векторы, так и переменные величины, которые они выражают, называют совпадающими по фазе. Векторная диаграмма и график двух величин, совпадающих по фазе, даны на рисунке 4.

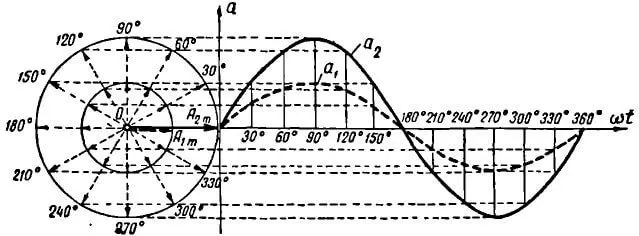
Рисунок 4. Построение двух синусоид путем вращения двух совпадающих векторов

Уравнения для таких величин запишутся так:

Если векторы сдвинуть один относительно другого на определенный угол φ и вращать вокруг точки 0, то мы получим две синусоидальные кривые, сдвинутые, как говорят, по фазе между собой на тот же угол φ. На рисунке 5 показано построение двух синусоид, сдвинутых по фазе на угол φ, равный 90°. В этом случае о кривой a₁ говорят, что она опережает кривую a₂ по фазе на 90°, или, наоборот, кривая a₂ отстает по фазе от кривой a₁ на 90°.

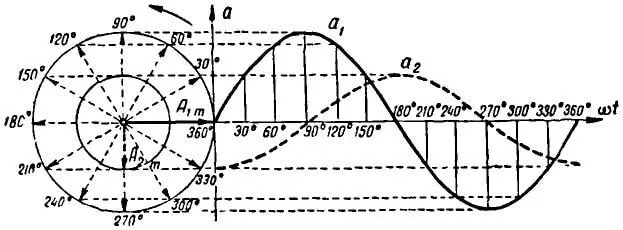
Рисунок 5. Построение двух синусоид, сдвинутых на угол 90°, путем вращения двух векторов, расположенных под углом 90°

При изучении явлений в цепях переменного тока приходится часто заниматься сложением и вычитанием синусоидальных величин (токов, напряжений и других).

Рассмотрим сложение двух синусоидальных величин, заданных уравнениями:

Их сумма будет иметь величину:

Произведя необходимые математические преобразования, получим окончательно:

Отсюда видно, что суммой двух синусоид одинакового периода является также синусоидой с амплитудой A_m и начальной фазой ψ.

Сложение синусоидальных величин проще представить на векторной диаграмме, показанной на рисунке 6 слева. Из диаграммы следует:

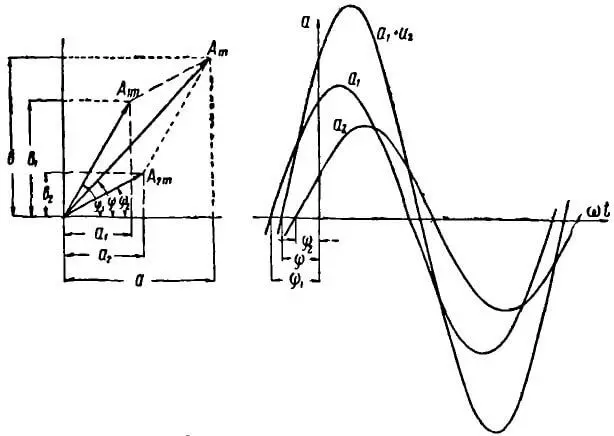
Рисунок 6. Сложение двух синусоидальных величин

Величина результирующего вектора A_m, равна геометрической сумме векторов A_1m и A_2m, составляет:

На рисунке 6 справа дано графическое сложение двух синусоидальных величин. Любое мгновенное значение результирующей синусоиды равно сумме мгновенных значений слагаемых синусоид для каждого момента времени.

Полученные выводы можно применить для сложения трех и больше синусоидальных величин.

Для того чтобы отличить действия с векторами от действий со скалярными величинами, мы в дальнейшем будем ставить черту над буквенным обозначением вектора. Например, сложение двух векторов A₁ и A₂ будем записывать так:

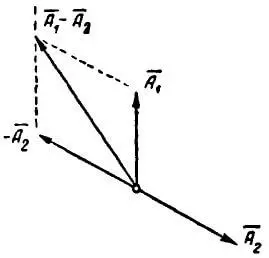
Рассмотрим теперь, как производится вычитание векторных величин. Пусть векторы A₁ и A₂ изображают какие-то синусоидальные величины и нам нужно из вектора A₁ вычесть вектор A₂ (рисунок 7). Вычитание векторов всегда можно заменить сложением уменьшаемого вектора с вектором, равным и противоположным вычитаемому вектору, то есть

Источник: Кузнецов М. И., "Основы электротехники" - 9-е издание, исправленное - Москва: Высшая школа, 1964 - 560 с.

Читайте также: