Сформулируйте и докажите теорему об окружности описанной около правильного многоугольника кратко
Обновлено: 04.07.2024
Пусть A и B – две соседние вершины правильного многоугольника. Проведем биссектрисы углов многоугольника из вершин A и B . Пусть O – точка их пересечения. Треугольник AOB – равнобедренный с основанием AB и углами при основании, равными α / 2 , где α – градусная мера угла многоугольника. Соединим точку O с вершиной C , соседней с B . Треугольники AOB и BOC равны по первому признаку равенства треугольников ( теорема 4.1 ), так как AB = BC , OB – общая сторона, OBC = α / 2 = OBA . Отсюда имеем OC = OB = OA . OCB = α / 2 . Так как C = α , то CO – биссектриса угла C. Аналогично, рассматривая последовательно вершины, соседние с ранее рассмотренными, получаем, что каждый треу гольник, у которого одна сторона – сторона многоугольника, а противолежащая вершина – точка O , является равнобедренным. Все эти треугольники имеют равные боковые стороны и равные высоты, опущенные на основания. Отсюда следует, что все вершины треугольника равноудалены от точки O на расстояние длины боковой стороны и лежат на одной окружности, а все стороны многоугольника касаются окружности с центром в точке O и радиусом, равным высотам треугольников, опущенным из вершины O .
Правильный многоугольник — выпуклый многоугольник, у которого все стороны и все углы равны между собой (Рис. 1).

Рисунок 1. Правильные многоугольники
Как мы знаем, сумма углов многоугольника находится по формуле$(n-2)\cdot ^0$
Значит, градусная мера одного угла правильного многоугольника равняется
Теорема об описанной около правильного многоугольника окружности
Около любого правильного многоугольника можно описать единственную окружность.
Доказательство.
Существование. Пусть нам дан правильный многоугольник $A_1A_2A_3\dots A_n$. Пусть биссектрисы углов $A_1\ и\ A_2$ пересекаются в точке $O$. Соединим с этой точкой все остальные вершины правильного многоугольника (Рис. 2).

Рисунок 2. Описанная вокруг правильного многоугольника окружность
Так как углы $A_1\ и\ A_2$ равны и $A_1O\ и\ A_2O$ — биссектрисы, то угол $OA_1A_2$ равен углу $O_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.
Аналогично доказывают другие равенства. В результате, будем иметь
То есть точка $O$ равноудалена от всех вершин многоугольника, а, значит, точка $O$ — центр описанной вокруг правильного многоугольника окружности.
Единственность. Рассмотрим три вершины многоугольника. Очевидно, что через них проходит только одна окружность, следовательно, вокруг правильного многоугольника можно описать только одну окружность.
Готовые работы на аналогичную тему
Теорема доказана.
Теорема вписанной в правильный многоугольник окружности
В любой правильный многоугольник можно вписать единственную окружность.
Доказательство.
Пусть нам дан правильный многоугольник $A_1A_2A_3\dots A_n$. Пусть точка $O$ — центр описанной вокруг данного многоугольника окружности (Рис. 3).

Рисунок 3. Вписанная в правильный многоугольник окружность
Так как углы $A_1\ и\ A_2$ равны и $A_1O\ и\ A_2O$ — биссектрисы, то угол $OA_1A_2$ равен углу $O_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.
Аналогично доказывается равенство других треугольников. То есть, мы получим
Значит и высоты этих треугольников равны между собой
Тогда окружность с центром в точке $O$ и радиусом, равным $ _1$ проходит через точки $H_1,\ H_2,\dots ,H_n$, то есть касается всех сторон данного многоугольника. Следовательно. Является вписанной для правильного многоугольника.
Единственность. Предположим противное. Пусть существует еще одна вписанная в этот многоугольник окружность. Обозначим её центр $O’$. Тогда $O’$ равноудалена от всех сторон многоугольника, а значит лежит в точке пересечения биссектрис его углов. Но тогда точка $O’$ совпадает с точкой $O$ и, следовательно, эти окружности также совпадают.
Теорема доказана.
Из этих двух теорем можно сформулировать следующие следствия:
Следствие 1: Вписанная в правильный многоугольник окружность касается его в серединах его сторон.
Следствие 2: Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в этот же правильный многоугольник. Этот центр называется центром правильного многоугольника.
Формулы для правильного многоугольника
Дадим теперь несколько формул, относящихся к понятию правильного многоугольника (без их вывода).
Введем следующие обозначения. Пусть $S$ — площадь правильного многоугольника, $P$ — периметр правильного многоугольника, $a$ — сторона правильного многоугольника, $r$ — радиус вписанной в правильный многоугольник окружности, $R$ — радиус описанной около правильного многоугольника окружности. Тогда
Пример задачи на понятие правильного многоугольника
Чему равна сумма внешних углов правильного $n$-угольника. Если при каждой вершине взят только один внешний угол.
Решение.
Очевидно, что все внешние углы будут равны между собой и их количество равно $n$. Найдем один из них. Внешний угол $\beta $ многоугольника будет смежным с внутренним углом многоугольника. Используя формулу нахождения угла правильного $n$-угольника $\alpha =\frac ^0(n-2)> $, получим
Значит, сумма всех внешних углов равна
Ответ: $ ^0.$
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 15 04 2021
Окружность: описанная около многоугольника
Определение
Окружность \(S\) описана около многоугольника \(P\) , если все вершины многоугольника \(P\) лежат на окружности \(S\) .
В этом случае многоугольник \(P\) называется вписанным в окружность.
Определение
Серединный перпендикуляр к отрезку – это прямая, проходящая через середину данного отрезка перпендикулярно ему.
Теорема
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Доказательство
Рассмотрим отрезок \(AB\) и серединный перпендикуляр \(a\) к нему. Докажем, что для любой точки \(X\in a\) выполнено: \(AX=BX\) .

Рассмотрим \(\triangle AXB\) : отрезок \(XO\) является медианой и высотой, следовательно, \(\triangle AXB\) – равнобедренный, следовательно, \(AX=BX\) .
Теорема
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Доказательство
Рассмотрим \(\triangle ABC\) . Проведем серединные перпендикуляры к сторонам \(AB\) и \(AC\) . Они пересекутся в точке \(O\) .

По предыдущей теореме для серединного перпендикуляра \(C_1O\) выполнено: \(AO=BO\) , а для \(B_1O\) — \(AO=CO\) . Следовательно, \(BO=CO\) . Значит, \(\triangle BOC\) – равнобедренный, следовательно, высота \(OA_1\) , проведенная к основанию \(BC\) , будет также и медианой. Значит, \(OA_1\) – серединный перпендикуляр к отрезку \(BC\) .
Таким образом, все три серединных перпендикуляра пересеклись в одной точке \(O\) .
Следствие
Если точка равноудалена от концов отрезка, то она лежит на его серединном перпендикуляре.
Теорема
Около любого треугольника можно описать единственную окружность, причём центр описанной окружности есть точка пересечения серединных перпендикуляров к сторонам треугольника.
Доказательство
Из доказанной выше теоремы следует, что \(AO=BO=CO\) . Значит, все вершины треугольника равноудалены от точки \(O\) , следовательно, они лежат на одной окружности.

Такая окружность единственна. Допустим, что около \(\triangle ABC\) можно описать еще одну окружность. Тогда ее центр должен совпасть с точкой \(O\) (т.к. это единственная точка, равноудаленная от вершин треугольника), а радиус должен быть равен расстоянию от центра до какой-то из вершин, т.е. \(OA\) . Т.к. у этих окружностей совпадают и центр, и радиус, то и эти окружности совпадают.
Теорема о площади вписанного треугольника
Если \(a, b, c\) – стороны треугольника, а \(R\) – радиус описанной около него окружности, то площадь треугольника \[S_ =\dfrac \]
Доказательство*
С доказательством данной теоремы рекомендуется ознакомиться после изучения темы “Теорема синусов”.
Обозначим угол между сторонами \(a\) и \(c\) за \(\alpha\) . Тогда \(S_ =\frac12 ac\cdot \sin \alpha\) .
По теореме синусов \(\dfrac b =2R\) , откуда \(\sin \alpha=\dfrac b \) . Следовательно, \(S_ =\dfrac \) .
Теорема
Около четырёхугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны \(180^\circ\) .
Доказательство


Опишем окружность около треугольника \(ABC\) . Пусть центр этой окружности – точка \(O\) . На прямой, проходящей через точки \(O\) и \(D\) отметим точку \(D’\) пересечения этой прямой и окружности. Предположим, что точки \(D\) и \(D’\) не совпали, тогда рассмотрим четырёхугольник \(CD’AD\) .
Углы \(CD’A\) и \(CDA\) дополняют угол \(ABC\) до \(180^\circ\) ( \(\angle CDA\) дополняет по условию, а \(\angle CD’A\) по доказанному выше), следовательно, они равны, но тогда сумма углов четырёхугольника \(AD’CD\) больше \(360^\circ\) , чего быть не может (сумма углов это четырёхугольника есть сумма углов двух треугольников), следовательно, точки \(D\) и \(D’\) совпадают.
Замечание. На рисунке точка \(D\) лежит вне круга, ограниченного окружностью, описанной около \(\triangle ABC\) , однако, в случае, когда \(D\) лежит внутри, доказательство также остаётся верным.
Теорема
Около выпуклого четырехугольника \(ABCD\) можно описать окружность тогда и только тогда, когда \(\angle ABD=\angle ACD\) .

Доказательство
Необходимость. Если около \(ABCD\) описана окружность, то углы \(\angle ABD\) и \(\angle ACD\) – вписанные и опираются на одну дугу \(\buildrel\smile\over\) , следовательно, они равны.
Достаточность. Пусть \(\angle ABD=\angle ACD=\alpha\) . Докажем, что около \(ABCD\) можно описать окружность.

Опишем окружность около \(\triangle ABD\) . Пусть прямая \(CD\) пересекла эту окружность в точке \(C’\) . Тогда \(\angle ABD=\angle AC’D \Rightarrow \angle AC’D=\angle ACD\) .
Следовательно, \(\angle CAD=\angle C’AD=180^\circ-\angle ADC-\angle AC’D\) , то есть \(\triangle AC’D=\triangle ACD\) по общей стороне \(AD\) и двум прилежащим углам ( \(\angle C’AD=\angle CAD\) , \(\angle ADC’=\angle ADC\) – общий). Значит, \(DC’=DC\) , то есть точки \(C’\) и \(C\) совпадают.
Теоремы
1. Если около параллелограмма описана окружность, то он – прямоугольник (рис. 1).
2. Если около ромба описана окружность, то он – квадрат (рис. 2).
3. Если около трапеции описана окружность, то она равнобедренная (рис. 3).

Верны и обратные утверждения: около прямоугольника, ромба и равнобедренной трапеции можно описать окружность, и притом только одну.
Доказательство
1) Пусть около параллелограмма \(ABCD\) описана окружность. Тогда суммы его противоположных углов равны \(180^\circ: \quad \angle A+\angle C=180^\circ\) . Но в параллелограмме противоположные углы равны, т.к. \(\angle A=\angle C\) . Следовательно, \(\angle A=\angle C=90^\circ\) . Значит, по определению \(ABCD\) – прямоугольник.
Обратное утверждение очевидно.
2) Пусть около ромба \(MNKP\) описана окружность. Аналогично предыдущему пункту (т.к. ромб является параллелограммом) доказывается, что \(MNKP\) – прямоугольник. Но все стороны этого прямоугольника равны (т.к. он ромб), значит \(MNKP\) – квадрат.
Обратное утверждение очевидно.
3) Пусть около трапеции \(QWER\) описана окружность. Тогда \(\angle Q+\angle E=180^\circ\) . Но из определения трапеции следует, что \(\angle Q+\angle W=180^\circ\) . Следовательно, \(\angle W=\angle E\) . Т.к. углы при основании \(WE\) трапеции равны, то она равнобедренная.
Окружность, описанная около правильного многоугольника
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти


Этот урок поможет вспомнить, какую окружность называют описанной около многоугольника. Будет доказана теорема об окружности, описанной около правильного многоугольника. А также рассмотрены задачи на применение полученных знаний.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Окружность, описанная около правильного многоугольника"
На этом уроке мы вспомним, какую окружность называют описанной около многоугольника. Докажем теорему об окружности, описанной около правильного многоугольника.

Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны. Так как у правильного многоугольника все углы равны, то угол правильного n-угольника можно вычислить по формуле: альфа энное равно 180 градусов умножить на эн минус два деленное на н, где n – количество сторон (углов) правильного n-угольника.
И вспомним еще определение описанной окружности.
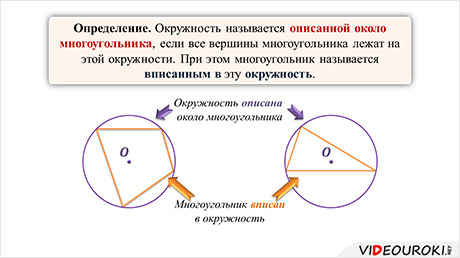
Определение. Окружность называется описанной около многоугольника, если все вершины многоугольника лежат на этой окружности. При этом многоугольник называется вписанным в эту окружность.
Докажем теорему об окружности, описанной около правильного многоугольника.
Теорема. Около любого правильного многоугольника можно описать окружность, и притом только одну.
Доказательство.
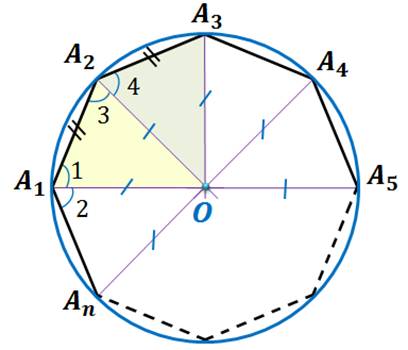

Пусть – правильный многоугольник.

Рассмотрим .
Так как ,то .

Следовательно, – равнобедренный.

Значит, .
Рассмотрим и .

– общая сторона и .

Следовательно, по двум сторонам и углу между ними.

Отсюда, .

Тогда точка равноудалена от всех вершин многоугольника.
Значит, окружность с центром в точке и радиусом является описанной

.

Тогда точка равноудалена от всех вершин многоугольника.
Значит, окружность с центром в точке и радиусом является описанной около многоугольника.
Рассмотрим вершины , и .

Так как через эти точки проходит только одна окружность, можно описать только одну окружность.
Теорема доказана.
Задача. Правильный многоугольник вписан в окружность с центром в точке . Длина одной стороны многоугольника равна см. Найдите периметр правильного многоугольника , если .
Решение. Так как у правильного многоугольника все стороны равны, то для нахождения периметра нужно знать число его сторон.

Пусть многоугольник имеет сторон.


Рассмотрим .

Точка равноудалена от всех вершин многоугольника.

Значит, .

Следовательно, – равнобедренный.





(см)

Ответ: (см).
Подведем итоги урока. На этом уроке доказали теорему об окружности, описанной около правильного многоугольника. А именно, что около любого правильного многоугольника можно описать окружность, и притом только одну.
Правильный многоугольник -- выпуклый многоугольник, у которого все стороны и все углы равны между собой (Рис. 1).

Рисунок 1. Правильные многоугольники
Как мы знаем, сумма углов многоугольника находится по формуле$(n-2)\cdot ^0$
Значит, градусная мера одного угла правильного многоугольника равняется
Теорема об описанной около правильного многоугольника окружности
Около любого правильного многоугольника можно описать единственную окружность.
Доказательство.
Существование. Пусть нам дан правильный многоугольник $A_1A_2A_3\dots A_n$. Пусть биссектрисы углов $A_1\ и\ A_2$ пересекаются в точке $O$. Соединим с этой точкой все остальные вершины правильного многоугольника (Рис. 2).

Рисунок 2. Описанная вокруг правильного многоугольника окружность
Так как углы $A_1\ и\ A_2$ равны и $A_1O\ и\ A_2O$ -- биссектрисы, то угол $OA_1A_2$ равен углу $O_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.
Так как $A_1A_2=A_2A_3$, $\angle O_1=\angle O_3$ и сторона $A_2O$ - общая, то треугольники $O_1$ и $O_3$ равны. Следовательно, $OA_2=OA_3$.
Аналогично доказывают другие равенства. В результате, будем иметь
То есть точка $O$ равноудалена от всех вершин многоугольника, а, значит, точка $O$ - центр описанной вокруг правильного многоугольника окружности.
Единственность. Рассмотрим три вершины многоугольника. Очевидно, что через них проходит только одна окружность, следовательно, вокруг правильного многоугольника можно описать только одну окружность.
Готовые работы на аналогичную тему
Теорема доказана.
Теорема вписанной в правильный многоугольник окружности
В любой правильный многоугольник можно вписать единственную окружность.
Доказательство.
Пусть нам дан правильный многоугольник $A_1A_2A_3\dots A_n$. Пусть точка $O$ - центр описанной вокруг данного многоугольника окружности (Рис. 3).

Рисунок 3. Вписанная в правильный многоугольник окружность
Так как углы $A_1\ и\ A_2$ равны и $A_1O\ и\ A_2O$ -- биссектрисы, то угол $OA_1A_2$ равен углу $O_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.
Так как $A_1A_2=A_2A_3$, $\angle O_1=\angle O_3$ и сторона $A_2O$ - общая, то треугольники $O_1$ и $O_3$ равны.
Аналогично доказывается равенство других треугольников. То есть, мы получим
Значит и высоты этих треугольников равны между собой
Тогда окружность с центром в точке $O$ и радиусом, равным $_1$ проходит через точки $H_1,\ H_2,\dots ,H_n$, то есть касается всех сторон данного многоугольника. Следовательно. Является вписанной для правильного многоугольника.
Единственность. Предположим противное. Пусть существует еще одна вписанная в этот многоугольник окружность. Обозначим её центр $O'$. Тогда $O'$ равноудалена от всех сторон многоугольника, а значит лежит в точке пересечения биссектрис его углов. Но тогда точка $O'$ совпадает с точкой $O$ и, следовательно, эти окружности также совпадают.
Теорема доказана.
Из этих двух теорем можно сформулировать следующие следствия:
Следствие 1: Вписанная в правильный многоугольник окружность касается его в серединах его сторон.
Следствие 2: Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в этот же правильный многоугольник. Этот центр называется центром правильного многоугольника.
Формулы для правильного многоугольника
Дадим теперь несколько формул, относящихся к понятию правильного многоугольника (без их вывода).
Введем следующие обозначения. Пусть $S$ -- площадь правильного многоугольника, $P$ -- периметр правильного многоугольника, $a$ - сторона правильного многоугольника, $r$ - радиус вписанной в правильный многоугольник окружности, $R$ - радиус описанной около правильного многоугольника окружности. Тогда
Пример задачи на понятие правильного многоугольника
Чему равна сумма внешних углов правильного $n$-угольника. Если при каждой вершине взят только один внешний угол.
Решение.
Очевидно, что все внешние углы будут равны между собой и их количество равно $n$. Найдем один из них. Внешний угол $\beta $ многоугольника будет смежным с внутренним углом многоугольника. Используя формулу нахождения угла правильного $n$-угольника $\alpha =\frac^0(n-2)>$, получим
Читайте также:

