Сформулируйте и докажите теорему о перпендикуляре проведенном из данной точки к данной прямой кратко

Обновлено: 01.07.2024

Теорема – утверждение, справедливость которого устанавливается путём рассуждений.

Отрезок – часть прямой, ограниченная двумя точками.

Перпендикуляр к прямой – это отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения.

Основная литература:

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Погорелов А. В. Геометрия: 7–9 класс. // Погорелов А. В. – М.: Просвещение, 2017. – 224 с.

Дополнительная литература:

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Ножки стола крепятся перпендикулярно столешнице. Маятник часов расположен перпендикулярно верхней стенке часов.

Если считать улицу, набережную реки Фонтанки, ребро столешницы, ребро стенки часов моделями прямых, то можно говорить, что на каждой картинке построены перпендикуляры к прямой.

Примеры с картой и пешеходным переходом иллюстрируют тот факт, что перпендикуляр к прямой – это кратчайший путь от точки до прямой. Такой путь называется расстоянием.

Пример с часами поможет нам запомнить происхождение слова перпендикуляр. В переводе с французского перпендикуляр означает висеть. То есть, перпендикуляр – это отвес.

Дадим определение перпендикуляра к прямой.

Мы знаем, что перпендикулярными прямыми называются две пересекающиеся прямые, которые образуют при пересечении четыре прямых угла.

Часть одной из этих прямых является перпендикуляром к прямой.

Выделенная часть прямой ограничена двумя точками, значит, по определению, – это отрезок. Один из концов этого отрезка является точкой пересечения перпендикуляра и прямой, к которой он проведен.

Определение:

перпендикуляр к прямой – это отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения.

Н – основание перпендикуляра.

Предположим, что вы купаетесь в море недалеко от берега. Вдруг появилась акула, необходимо срочно плыть к берегу. Конечно, вы выберите самый короткий путь. А мы уже знаем, что в геометрии этот путь называют перпендикуляром к прямой.

Всегда ли можно найти кратчайший путь? Сколько существует способов построения кратчайшего пути?

Если на пути нет препятствий, например, здания, ямы, в данном примере – других пловцов, то самый короткий путь проделать можно. И такой путь единственный.

В геометрии любое утверждение требует доказательства. Сформулируем теорему о перпендикуляре к прямой.

Теорема: из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

По условию теоремы нам даны прямая и точка.

Заключение теоремы состоит из двух частей – существование перпендикуляра и его единственность.

1.Через точку А можно провести перпендикуляр к прямой BC.

2.Данный перпендикуляр единственный.

Допустим, существует другой перпендикуляр AH₁ →AH⊥BC и AH₁⊥BC, это невозможно.

Разбор заданий тренировочного модуля.

Задание 1. Построить перпендикуляр к прямой.

Для этого можно использовать чертёжный угольник, одну сторону которого от угла в 90 градусов прикладываем к прямой, к которой проведём перпендикуляр из точки, не лежащей на этой прямой, а вторую сторону угольника совместим с точкой, от которой проведём перпендикуляр к прямой.

Задание 2. На рисунке изображены два перпендикуляра АB и СD к прямой а, при этом АB = СD.

Докажем, что треугольники ABD и CDВ равны.

По условию в треугольниках ABD и CDВ, сторона АBравна стороне СD.

AB ⊥ а =>∠ABD = 90° (по определению перпендикулярных прямых).

СD ⊥ а => ∠CDВ = 90° (по определению перпендикулярных прямых).

Следовательно, ∠ABD = ∠CDВ.

Сторона BD – общая,

Следовательно, ∆ABD = ∆CDВ

(по первому признаку равенства треугольников: по двум сторонам и углу между ними).

На данном уроке рассказываем о перпендикуляре к прямой. Приводим формулировку и доказательство теоремы о существовании единственного перпендикуляра, проведённого из точки к прямой. Также показываем, как провести перпендикуляр с помощью чертёжного угольника. И напоследок решаем задачу.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Перпендикуляр к прямой"

Рассмотрим понятие перпендикуляра к прямой. Возьмём прямую а и некоторую точку О, которая не лежит на этой прямой. Соединим точку О с точкой В, которая лежит на прямой а.

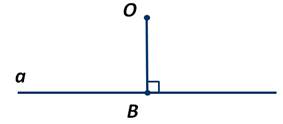
Отрезок ОВ называется перпендикуляром, проведённым из точки В к прямой а, если отрезок ОВ и прямая а перпендикулярны. Точку В называют основанием перпендикуляра.

Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

1. Существование перпендикуляра.

Пусть точка А не лежит на прямой p. Возьмём на этой прямой точку О и проведём луч ОA. Затем от луча ОB отложим угол BОK, равный углу АОВ. На луче ОK отложим отрезок ОС, равный отрезку ОA.

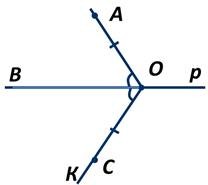
Пусть точка D - точка пересечения отрезка AС и прямой p. ∆ AOD=∆ COD по первому признаку, так как сторона ОD у них общая, ∠AОD=∠COD и ОA=ОС. Следовательно, ∠СDO=∠ADO. А так как углы СDO и ADO являются смежными, то ∠СDO=∠ADO и равняется 90 градусов. Значит, отрезок AD перпендикулярен прямой p, то есть перпендикуляр существует.

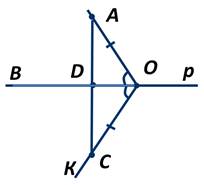
2. Единственность перпендикуляра.

Предположим, что из точки А можно провести ещё один перпендикуляр АD₁ к прямой р. Пусть CD - луч, противоположный лучу АD, и АD=CD.

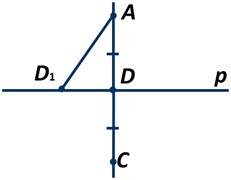
Треугольник ADD₁ равен треугольнику СDD₁ по первому признаку, так как сторона DD₁ у них общая, сторона АD=СD, ∠ADD₁=∠СDD₁. Следовательно, ∠AD₁D=∠СD₁D.

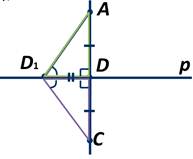
Так как по предположению ∠AD₁D=90 градусов, то и ∠СD₁D=90 градусов, то есть ∠АD₁С развёрнутый и лучи D₁А и D₁С составляют прямую. Таким образом, получили, что через две точки А и С проходят две прямые, а ранее мы говорили, что это невозможно. Следовательно наше предположение неверно, то есть из точки А к прямой р можно провести только один перпендикуляр. Теорема доказана.

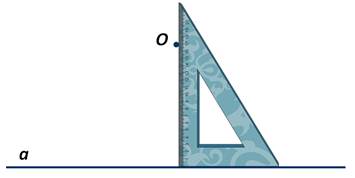
Чтобы провести перпендикуляр из точки О к прямой а используют чертёжный угольник.

Точки M и N лежат по одну сторону от прямой q. Перпендикуляры МО и NP, проведённые к прямой q равны. Найти градусную меру ∠NPM, если ∠NOP=35 градусов.

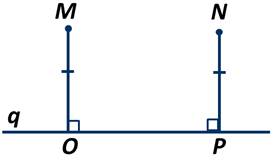
Рассмотрим треугольники MOP и NPO. У них сторона OР - общая, сторона МО=NP по условию задачи, а ∠MOP=∠NPO и их градусная мера равна 90 градусов, так как MO и NP - перпендикуляры.

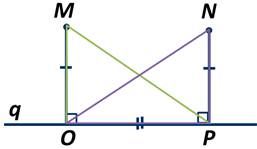
Следовательно, ∆ MOP=∆ NPO по первому признаку равенства треугольников. Значит, у них соответственные стороны и углы равны. Тогда ∠NOP=∠MPO=35 0 .

∠NPO=∠NPM+∠MPO. Из этого равенства получаем, что ∠NPM=∠NPO-∠MPO.

Нам известно, что ∠NPO=90 градусов, так как NP - перпендикуляр, а ∠MPO=35 градусов.

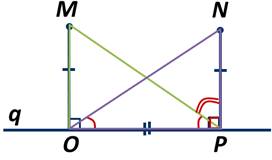
Получаем, что ∠NPМ=90 0 -35 0 . То есть градусная мера искомого угла равна 55 градусов.

Сформулируйте и докажите теорему о перпендикуляре, проведённом из данной точки к данной прямой.

Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и притом только один.

Доказательство : предположим, что на плоскости, которой принадлежат и прямая, и точка, таких перпендикуляров существует два.

Поскольку точка вне прямой принадлежит обоим перпендикулярам, получаем треугольник с вершиной в этой точке и основанием, расположенном на прямой.

Так как оба перпендикуляра составляют с прямой углы по 90° (углы при основании треугольника) плюс угол при вершине, то сумма внутренних углов такого треугольника получается больше 180°, - а это на плоскости осуществить невозможно.

Следовательно, наше предположение о том, что через одну точку к данной прямой на плоскости можно провести больше одного перпендикуляра, - не верно и такой перпендикуляр существует только один.

PS построения не сложные.

- прямая, 2 точки на ней, одна точка вне прямой и два отрезка, соединяющие эту точку с точками на прямой.

))) Но, если очень надо, - то файлик внизу с рисунком.

Упоминание о том, что все это происходит на плоскости, - желательно.

Дело в том, что всем нам с детства знакомы меридианы на географической сетке Земного шара.

Так вот каждый меридиан перпендикулярен экватору, и все меридианы сходятся аж в двух точках : в Северном и Южном полюсах.

Пусть задана прямая a и точка A, не лежащая на этой прямой (Рис.1).

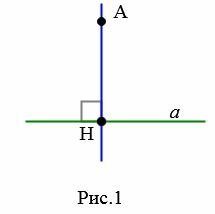Отметим на прямой a точку H и соединяющие точки A и H. Отрезок AH называется перпендикуляром проведенным от точки A к прямой a, если прямые a и AH перпендикулярны. Точка H называется основанием перпендикуляра.

Теорема 1. Из точки, не лежащей на данной прямой можно провести перпендикуляр к этой прямой, и причем единственный.

Доказательство. Пусть задана прямая BC и точка A, не лежащая на этой прямой (Рис.2).

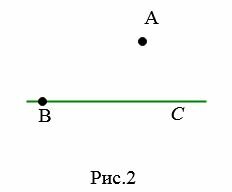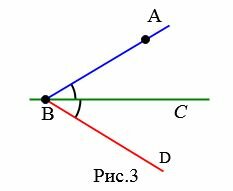Докажем, сначала, что из точки A можно провести перпендикуляр к прямой BC. Проведем луч BA и отложим от луча BC угол DBC, равной углу ABC (Рис.3). Поскольку \( \small ∠ ABC=∠ DBC,\) то первый из них можно наложить на вторую. При этом точка A наложится на некоторую точку A₁ луча BD (Рис.4).

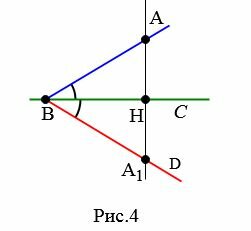Обозначим через H точку пересечения прямых AA₁ и BC. Таким образом при наложении угла ABC на угол DBC, точка A наложилась на точку A₁. Тогда AH наложится на A₁H, угол AHB наложится на угол A₁HB. Следовательно \( \small ∠ AHB=∠ A_1HB.\) Но углы AHB и A₁HB смежные, значит \( \small ∠ AHB+∠ A_1HB=180°.\) Таким образом \( \small ∠ AHB=∠ A_1HB=90°.\) Тогда AH пернпендикуляр к прямой BC от точки A, т.е. \( \small AH⊥ BC.\)

Докажем, далее, что из точки A можно провести только один перпендикуляр к прямой BC.

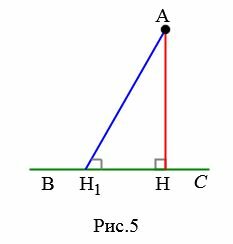Предположим, что из точки A можно провести еще один перпендикуляр AH₁ (Рис.5). Тогда получим, что две прямые AH и AH₁ перпендикулярные к прямой BC пересекаются. Но это противоречит тому, что если две прямые перпендикулярны к третьей, то они не пересекаются (теорема 1 статьи Перпендикулярные прямые). Следовательно из точки A можно провести только один перпендикуляр к прямой BC.

Читайте также: