Сечение это в геометрии кратко
Обновлено: 02.07.2024
Правила построения сечений многогранников:
1) проводим прямые через точки, лежащие в одной плоскости;
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого
а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
б) параллельные грани плоскость сечения пересекает по параллельным прямым.
Примеры построения сечений:
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L.
Соединим точки M и L, лежащие в плоскости AA1D1D.
Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C:
пересечем прямую ML (принадлежащую сечению) с ребром DD1, они лежат в одной плоскости AA1D1D, получим точку X2;
пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной плоскости A1B1C1D1, получим точку X3;
Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3 , которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.
MKNTPL - искомое сечение.
Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.
Соединим точки M и L, лежащие в плоскости AA1D1D.
Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.
Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.
Дополнительная литература:
Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.
Открытые электронные ресурс:
Теоретический материал для самостоятельного изучения
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются. Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.
Теорема о параллельности трех прямых: если a∥b, b∥c, то и a∥c. Определение: прямая и плоскость параллельны, если они не имеют общих точек. Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.
Определение: две плоскости параллельны, если они не имеют общих точек.
Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.
Если две плоскости пересекаются, то их линия пересечения — прямая.
Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)
Если плоскости α и β пересекаются по прямой a, а плоскости β и γ пересекаются по прямой b, причем a∥b, то плоскости α и γ пересекутся по прямой c∥a∥b.
Следом называется прямая, по которой плоскость сечения пересекает плоскость любой из граней многогранника.
Примеры и разбор решения заданий тренировочного модуля
№1 SABCD – четырехугольная пирамида, в основании которой лежит квадрат ABCD, а две боковые грани SAB и SAD представляют собой прямоугольные треугольники с прямым углом ∠A. Найдите площадь сечения пирамиды плоскостью α, если SA=AB=a.

сначала построим сечение по условию задачи.
1)Пусть AC∩BD=O. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Заметим, что т.к. ∠SAB=∠SAD=90∘⇒SA⊥(ABC). Проведем в плоскости SAC прямую OK∥SC. Т.к. O – середина AC, то по теореме Фалеса K – середина SA. Через точку K в плоскости SAB проведем KM∥SB (следовательно, M – середина AB). Таким образом, плоскость, проходящая через прямые OK и KM, и будет искомой плоскостью. Необходимо найти сечение пирамиды этой плоскостью. Соединив точки O и M, получим прямую MN. Т.к. α∥(SBC),то α пересечет плоскость SCD по прямой NP∥SC (если NP∩SC≠∅, то α∩(SBC)≠∅, что невозможно ввиду их параллельности). Таким образом, KMNP – искомое сечение, причем KP∥AD∥MN⇒ это трапеция.
2)Т.к. все точки K,M,N,P – середины отрезков SA,AB,CD,SD соответственно, то: а) MN=AD=a б) KP=1/2AD=a/2 в) KM=1/2SB=a 2/2 Заметим, что по теореме о трех перпендикулярах SB⊥BC⇒KM⊥MN. Таким образом, KMNP – прямоугольная трапеция. SKMNP=(KP+MN)* KM/ 2 =3 a 2 /8

Ответ:3 a 2 /8

боковая грань прямой призмы является прямоугольником.
Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.


То есть большая боковая грань содержит большую сторону основания.

Получим, что длина стороны АС=7см.
Зная большую сторону основания и площадь наибольшей боковой грани призмы, длину высоты призмы вычислить нетрудно.

Получим, что длина высоты призмы равна .

Найдем площадь основания, а оно равно площади сечения, по формуле .

Мы воспользуемся второй формулой. Получим, что площадь основания равна .

Ответ: 15 /4 см 2
№3 На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ:QB=1:2. Точка P — середина ребра AS.
Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.

пусть сторона основания пирамиды равна 3а, а высота пирамиды равна h. Тогда площадь сечения DSB равна
S=BD*SO/2= 3 =6
Площадь сечения DPQ равна


Дана правильная треугольная пирамида SABC с вершиной S. Через середину ребра AC и точки пересечения медиан граней ASB и CSB проведена плоскость. Найдите площадь сечения пирамиды этой плоскостью, если AB=21,AS=12 .

пусть LK∩SO=H. Тогда по теореме о трех перпендикулярах HK⊥AC как наклонная (HO⊥(ABC),OK⊥AC как проекция). Следовательно, и LK⊥AC.
Тогда SALC=AC⋅LK/2 Рассмотрим △SKB: BK=AB⋅ /2=21 /2⇒cosB=7 /12 .
Тогда по теореме косинусов для △KLB: KL 2 =729/4⇒KL=27/2
Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK : KA1 = 1 : 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD1 в точке M, АВ=4, АА1=6. Найдите площадь сечения.

По теореме о трех перпендикулярах прямые BM и AC перпендикулярны, а значит, прямые BM и KL перпендикулярны. Площадь четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения диагоналей. Найдем их: KL=AC=4 как диагональ квадрата, лежащего в основании призмы, тогда
по теореме Пифагора.


Ответ: 8
Сечение – планиметрическая фигура, образованная рассечением объемного тела. Сечение должно образовывать единую фигуру (быть замкнутым). Построение сечения делается по строгим правилам и принципам, которые, в свою очередь, основываются на аксиомы и теоремы стереометрии.
СЕЧЕНИЯ МНОГОГРАННИКОВ
Сечение многогранника плоскостью - плоский многоугольник, у которого:
- вершины принадлежат ребрам,
- а стороны – граням многогранника.
Две соседние вершины сечения принадлежат одной грани многогранника.
ПРИНЦИПЫ ПОСТРОЕНИЯ СЕЧЕНИЙ МНОГОГРАННИКОВ:
1. Если две точки сечения принадлежат одной грани, то эти точки можно соединить.

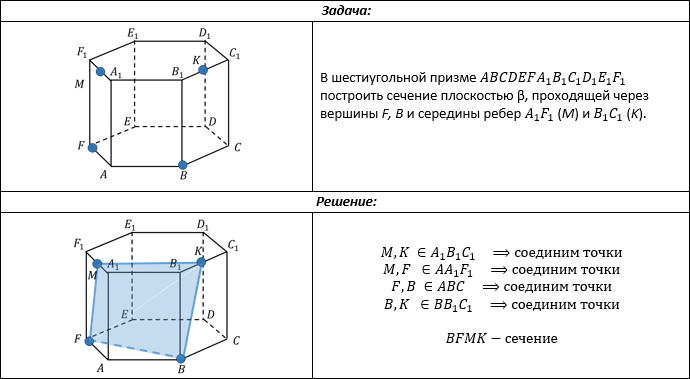

2. Если известна линия, по которой плоскость пересекает одну из параллельных граней, то вторую грань плоскость пересечет по линии, параллельной данной.

Большое значение для этого принципа имеет именно третье свойство – свойство параллельных плоскостей.
МЕТОД СЛЕДОВ

След –прямая l
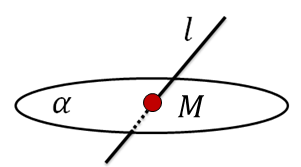
След плоскости на плоскости – прямая, по которой плоскость пересекает плоскость .
След прямой l на плоскости – точка пересечения прямой l с плоскостью .

СЕЧЕНИЯ ТЕЛ ВРАЩЕНИЯ:
ЦИЛИНДР
Характерные сечения цилиндра:

Другие варианты сечений (сечение - эллипс или часть эллипса):

КОНУС
Характерные сечения конуса:

Другие варианты сечений (сечение – эллипс или часть эллипса):

ШАР
Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Сечение – планиметрическая фигура, образованная рассечением объемного тела. Сечение должно образовывать единую фигуру (быть замкнутым). Построение сечения делается по строгим правилам и принципам, которые, в свою очередь, основываются на аксиомы и теоремы стереометрии.

СЕЧЕНИЯ МНОГОГРАННИКОВ
Сечение многогранника плоскостью - плоский многоугольник, у которого:
- вершины принадлежат ребрам,
- а стороны – граням многогранника.
Две соседние вершины сечения принадлежат одной грани многогранника.
ПРИНЦИПЫ ПОСТРОЕНИЯ СЕЧЕНИЙ МНОГОГРАННИКОВ:
1. Если две точки сечения принадлежат одной грани, то эти точки можно соединить.



2. Если известна линия, по которой плоскость пересекает одну из параллельных граней, то вторую грань плоскость пересечет по линии, параллельной данной.

Большое значение для этого принципа имеет именно третье свойство – свойство параллельных плоскостей.
МЕТОД СЛЕДОВ

След –прямая l

След плоскости на плоскости – прямая, по которой плоскость пересекает плоскость .
След прямой l на плоскости – точка пересечения прямой l с плоскостью .

СЕЧЕНИЯ ТЕЛ ВРАЩЕНИЯ:
ЦИЛИНДР
Характерные сечения цилиндра:

Другие варианты сечений (сечение - эллипс или часть эллипса):

КОНУС
Характерные сечения конуса:

Другие варианты сечений (сечение – эллипс или часть эллипса):

ШАР
Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Читайте также:

