Рациональная дробь это кратко
Обновлено: 07.07.2024
Урок 1: Рациональные дроби и их свойства. Основное свойство дроби. Сокращение дробей
Рациональные дроби и их свойства. Основное свойство дроби. Сокращение дробей.
Целые выражения – это выражения, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения 7а 2 b, m 3 +n 3 , a + 5 8 и т.д.
В отличие от них выражения 4 a - b 2 a + 1 , x + y x 2 - 3 xy + y 2 , помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.
Целые и дробные выражения называют рациональными выражениями.
Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.
Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение 10 + 1 a не имеет смысла при а = 0. При всех остальных значениях а это выражение имеет смысл. Выражение x x - y имеет смысл при тех значениях х и у, когда x ≠ y.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Выражение вида a b называется, как известно, дробью.
Дробь, числитель и знаменатель которой – многочлены, называют рациональной дробью.
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Пример 1. Найдем допустимые значения переменной в дроби 5 a ( a - 9 ) .
Чтобы найти, при каких значениях а знаменатель дроби обращается в нуль, нужно решить уравнение а(а - 9) = 0.
Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9.
Пример 2. При каком значении х значение дроби x - 2 2 - 25 2 x + 6 равно нулю?
Дробь a b равна нулю тогда и только тогда, когда a = 0 и b ≠ 0.
Числитель дроби равен нулю при x = 7 и x= -3. Знаменатель данной дроби не равен нулю, если x ≠ -3. Значит, данная дробь равна нулю при x = 7.
Мы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно paвенство a b = a ∙ c b ∙ c .
Докажем, что это равенство верно не только при натуральных, но и при любых других значениях а, b и с, при которых знаменатель отличен от нуля, т.е. при b ≠ 0 и с ≠ 0.
Пусть a b = m . Тогда по определению частного a = bm . Умножим обе части этого равенства на с:
На основании сочетательного и переместительного свойств умножения имеем:
Так как bс ≠ 0, то по определению частного
Мы показали, что для любых числовых значений переменных b и с, где b ≠ 0 и с ≠ 0, верно равенство a b = ac bc .
Равенство сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причем b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю.
Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.
Например, x + 2 x - 3 = ( x + 2 ) ( x + y ) ( x - 3 ) ( x + y ) .
Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.
Определение. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.
Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведем примеры.
Пример 3. Приведем дробь 2 x 7 y к знаменателю 35у 3 .
Так как 35у 3 = 7у·5у 2 , то, умножив числитель и знаменатель дроби 2 x 7 y на 5у 2 , получим:
2 x 7 y = 2 x · 5 y 2 7 y ∙ 5 y 2 = 10 x y 2 35 y 3
Множитель 5у 2 называют дополнительным множителем к числителю и знаменателю дроби 2 x 7 y .
Пример 4. Приведем дробь 5 2 y - x к знаменателю x - 2 y .
Для этого числитель и знаменатель данной дроби умножим на -1:
5 2 y - x = 5 · ( - 1 ) ( 2 y - x ) · ( - 1 ) = - 5 x - 2 y
Дробь - 5 x - 2 y можно заменить тождественно равным выражением - 5 x - 2 y , поставив знак "минус" перед дробью и заменив знак в числителе.
Если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.
Математика:
Контакты
Целые выражения - это выражения, составленные из чисел и переменных с использованием действий сложения, вычитания, умножения и деления на число, отличное от нуля.
Дробные выражения допускают также деление на выражение с переменными.
Целые и дробные выражения называют рациональными выражениями.
Допустимые значения переменных - это те значения переменных, при которых выражение имеет смысл.
Рациональная дробь - это дробь, числителем и знаменателем которой являются многочлены.
Основное свойство дроби: если числитель и знаменатель некоторой рациональной дроби умножить на один и тот же многочлен, не равный тождественно нулю, то получится дробь, равная исходной.
Тождество - это равенство, которое верно при всех допустимых значениях переменных, входящих в это равенство.
Свойства действий с рациональными дробями:
Если а, b, с — многочлены, причем многочлен c не равен нулю тождественно, то верно:
Если a, b,c,d- многочлены, причем многочлены b и d тождественно не равны нулю, то верно:
Если a, b, с, d - многочлены, причем многочлены b, с и d тождественно не равны нулю, то верно:
Пример 1. Сократите дробь $\frac$
Пример 2. Упростите выражение $\frac - \frac$
Пример 3. Упростите выражение $(\frac - \frac) \cdot \frac$
Пример 4. Выполните деление: $\frac : \frac$
subjects/mathematics/рациональные_дроби_и_их_свойства.txt · Последние изменения: 2013/02/01 20:36 — ¶
Инструменты страницы







Записаться на занятия

Записаться на занятия к репетитору

О чем эта статья:
6 класс, 8 класс
Определение рациональных чисел
Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Если число можно получить делением двух целых чисел, то это число рациональное.
Рациональные числа — это те, которые можно представить в виде
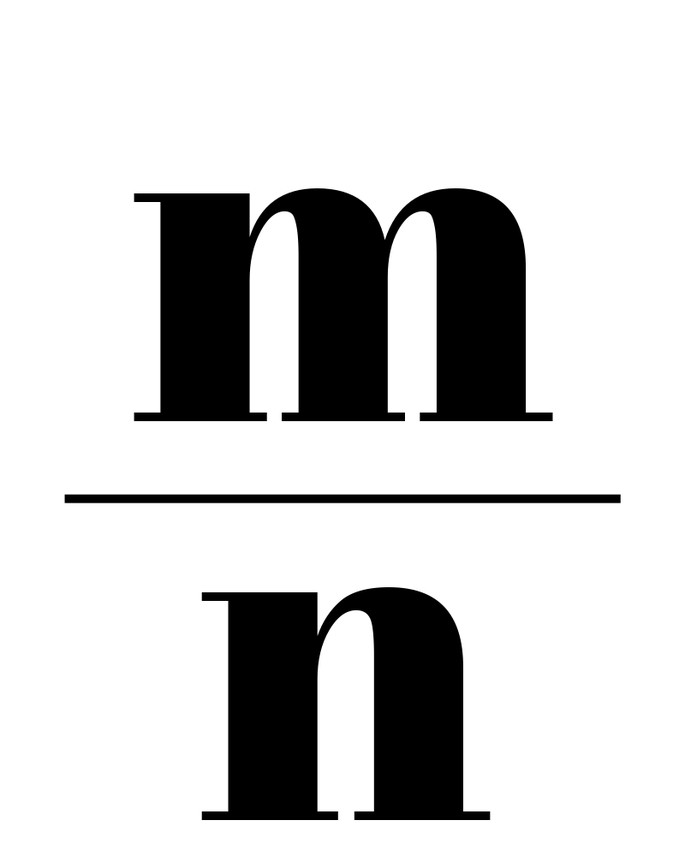
где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:

- десятичная дробь 1,15 — это 115/100;
- десятичная дробь 0,5 — это 1/2;
- целое число 0 — это 0/1;
- целое число 6 — это 6/1;
- целое число 1 — это 1/1;
- бесконечная периодическая дробь 0,33333. — это 1/3;
- смешанное число — это 25/10;
- отрицательная десятичная дробь -3,16 — это -316/100.
Свойства рациональных чисел
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
- Переместительное свойство сложения: a + b = b + a.
- Сочетательное свойство сложения: (a + b) +c = a + (b + c).
- Сложение рационального числа и нейтрального элемента (нуля) не изменяет это число: a + 0 = a.
- У каждого рационального числа есть противоположное число, а их сумма всегда равна нулю: a + (-a) = 0.
- Переместительное свойство умножения: ab = ba.
- Сочетательное свойство умножения: (a * b) * c = a * (b * c).
- Произведение рационального числа и едины не изменяет это число: a * 1 = a.
- У каждого отличного от нуля рационального числа есть обратное число. Их произведение равно единице: a * a−1 = 1.
- Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.
Кроме основных перечисленных есть еще ряд свойств:
Мы знаем, что 0 = d + (-d) для любого рационального d, значит a * 0 = a * (d + (-d)).
Распределительный закон позволяет переписать выражение:
a * d + a * (−d), а так как a * (−d) = -ad, то a * d + a * (-d) = a * d + (-ad).
Мы перечислили только свойства сложения и умножения. На множестве рациональных чисел вычитание и деление можно записать, как обратные к сложению и умножению. То есть, разность (a - b) можно записать, как сумму a + (-b), а частное a/b равно произведению a * b−1, при b ≠ 0.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Определение иррационального числа
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби
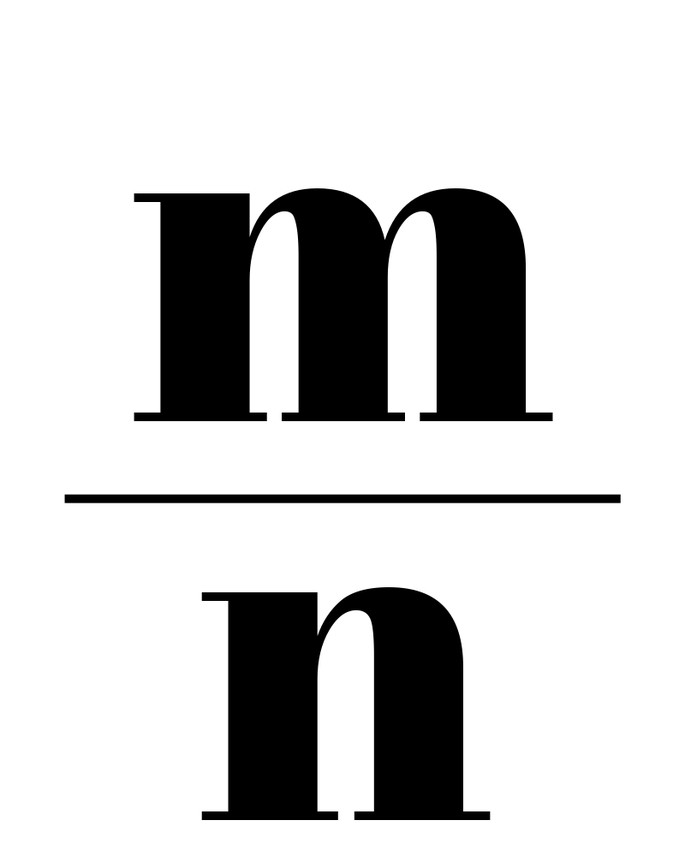
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
- π = 3,1415926.
- √2 = 1,41421356.
- e = 2,71828182…
- √8 = 2.828427.
- -√11= -3.31662…
Обозначение множества иррациональных чисел: латинская буква I.
Действительные или вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Свойства иррациональных чисел:
- результат суммы иррационального числа и рационального равен иррациональному числу;
- результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
- результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
- результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).
Различие между целыми, натуральными и рациональными числами
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое: один банан, две тетрадки, десять стульев.
А вот, что точно не является натуральным числом:
- Нуль — целое число, которое при сложении или вычитании с любыми числами в результате даст то же число. Умножение на ноль дает ноль.
- Отрицательные числа: -1, -2, -3, -4.
- Дроби: 1/2, 3/4, 5/6.
Целые числа — это натуральные числа, противоположные им и нуль.
Какие числа называются рациональными мы уже знаем из первой части статьи. Повторим еще раз.
Рациональные числа — это конечные дроби и бесконечные периодические дроби.
Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. Поэтому во множество рациональных чисел входит множество целых и натуральных чисел.

Но не все числа можно назвать рациональными. Например, бесконечные непериодические дроби не принадлежат множеству рациональных чисел. Так √3 или 𝜋 (число пи) нельзя назвать рациональными числами.
где P(x) и Q(x) некоторые многочлены.
Различают правильные и неправильные рациональные дроби, по аналогии с обычными числовыми дробями. Рациональная дробь называется правильной, если порядок знаменателя больше порядка числителя, и неправильной, если наоборот.
Любую неправильную рациональную дробь можно преобразовать в сумму некоторого многочлена и правильной рациональной дроби
(a — вещественный корень Q(x)) либо " width="" height="" />
(a, b — комплексные корни Q(x)) в степени, меньшей, либо равной кратности соответствующих корней в многочлене Q(x). На основании этого утверждения основана теорема об интегрируемости рациональной дроби. Согласно ей, любая рациональная дробь может быть интегрирована в элементарных функциях, что делает класс рациональных дробей весьма важным в математическом анализе.
eo:Frakcio (matematiko) nn brot pl:Ułamek simple:Fraction (mathematics)
Читайте также:


