Применение производной в математике кратко

Обновлено: 02.07.2024

Ведущая цель - показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.

Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.

Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.

Ключевой и тематический вопросы данного реферата:

1. История возникновения производной.

2. Зачем изучать производные функций?

3. Где используются производные?

4. Применение производных в физике, химии, биологии и других науках.

В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.

Применение производной в различных областях науки

Из курса алгебры старших классов мы уже знаем, что производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.

Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.

Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Физический смысл производной: производная функции y = f ( x ) в точке x ₀ – это скорость изменения функции f ( x ) в точке x ₀ .

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.

Геометрический смысл производной состоит в том, что производная функция в точке x ₀ равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x ₀ .

Термин производная и современные обозначения y ' , f ' ввёл Ж.Лагранж в 1797г.

С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:

Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;

Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;

Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.

Производная в алгебре:

1. Касательная к графику функции

Касательная к графику функции f, дифференцируемой в точке x _о , - это прямая, проходящая через точку (x _о ; f (x _о )) и имеющая угловой коэффициент f ′(x _о ).

2. Поиск промежутков возрастания и убывания функции

Функция y=f(x) возрастает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Функция y=f(x) убывает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

3. Поиск точек экстремума функции

Точку называют точкой максимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают .

Точку называют точкой минимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Под окрестностью точки понимают интервал , где - достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .

4. Поиск промежутков выпуклости и вогнутости функции

График функции , дифференцируемой на интервале , является на этом интервале выпуклым , если график этой функции в пределах интервала лежит не выше любой своей касательной (рис. 1).

График функции , дифференцируемой на интервале , является на этом интервале вогнутым , если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).

Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.

5. Поиск точек изгиба функции

Производная в физике:

1. Скорость как производная пути

2. Ускорение как производная скорости a =

3. Скорость распада радиоактивных элементов = - λN

А так же в физике производную применяют для вычисления:

Скорости материальной точки

Мгновенной скорости как физический смысл производной

Мгновенное значение силы переменного тока

Мгновенное значение ЭДС электромагнитной индукции

Максимальную мощность

Производная в химии:

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности . V (t) = p ‘(t)

в-ва в момент времени t 0

p = p(t 0 )

Интервал времени

∆ t = t– t 0

Приращение аргумента

Изменение количества в-ва

∆ p= p(t 0 + ∆ t ) – p(t 0 )

Приращение функции

Средняя скорость химической реакции

Отношение приращёния функции к приращёнию аргумента

Производная в биологии:

Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

Производная в географии:

Производная помогает рассчитать:

1. Некоторые значения в сейсмографии

2. Особенности электромагнитного поля земли

3. Радиоактивность ядерно- геоифзичексих показателей

4.Многие значения в экономической географии

5.Вывести формулу для вычисления численности населения на территории в момент времени t.

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует

Производная в электротехнике:

В наших домах, на транспорте, на заводах : всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

В электротехнике в основном используется работа переменного тока.

Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.

Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.

Производная в экономике:

Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.

Производная в экономике решает важные вопросы:

1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?

2. Увеличится или уменьшится выручка фирмы при увеличение цены на её продукцию?

Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления.

Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.

ВЫВОД: производная успешно применяется при решении различных прикладных задач в науке, технике и жизни

Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.

В заключении я хочу вам прочитать стихотворение:

“ Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.

Так сказал американский математик Морис Клайн.

Список используемой литературы:

1. Богомолов Н.В., Самойленко И.И. Математика. - М.: Юрайт, 2015.

2. Григорьев В.П., Дубинский Ю.А, Элементы высшей математики. - М.: Академия, 2014.

3. Баврин И.И. Основы высшей математики. - М.: Высшая школа, 2013.

4. Богомолов Н.В. Практические занятия по математике. - М.: Высшая школа, 2013.

5. Богомолов Н.В. Сборник задач по математике. - М.: Дрофа, 2013.

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная - одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того - это нужно делать. При решении примеров по математике возьмите за правило - если можете упростить выражение, обязательно упрощайте.

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Математика берет свои истоки со времен Античности. Благодаря ней архитектура, строительство и военное дело дали новый виток развития, достижения, которые были получены с помощью математики, привели к движению прогресса. И по сей день математика остается главной наукой, которая встречается во всех остальных отраслях.

Чтобы быть образованными, дети с первого класса начинают постепенно вливаться в эту среду. Очень важно разбираться в математике, так как она, в той или иной степени, встречается каждому человеку на протяжении всей его жизни. В этой статье будет разобран один из ключевых элементов - нахождение и применение производных. Не всякий человек может представить, насколько широко используется это понятие. Рассмотрим более 10 применений производных в определенных областях или науках.

Применение производной к исследованию функции

Производная - это такой предел отношения приращения функции к увеличению ее аргумента, когда показатель аргумента стремится к нулю. Производная - незаменимая вещь при исследовании функции. Например, с помощью нее можно определить возрастание и убывание последней, экстремумы, выпуклости и вогнутости. Дифференциальные исчисления входят в обязательную программу обучения студентов 1 и 2 курса математических вузов.

Область определения и нули функции

Первый этап любого исследования графика начинается с выяснения области определения, в более редких случаях - значения. Область определения задается по оси абсциссы, если говорить другими словами, то это числовые значения на оси OX. Часто область определения уже задана, но если она не задана, то следует оценить значение аргумента х. Допустим, если при каком-то значениях аргумента функция не имеет смысла, то этот аргумент исключается из области определения.

Нули функции находятся простым способом: функцию f(x) следует приравнивнять к нулю и решить полученное уравнение относительно одной переменной x. Полученные корни уравнения являются нулями функции, то есть в этих x функция равна 0.

Возрастание и убывание

Применение производной для исследования функций на монотонность может рассматриваться с двух позиций. Монотонная функция - это категория, которая имеет только положительные значения производной, либо только отрицательные. Простыми словами - функция только возрастает или только убывает на всем исследуемом промежутке:

Параметр возрастания. Функция f(x) будет возрастать, если производная f`(x) больше нуля.
Параметр убывания. Функция f(x) будет убывать, если производная f`(x) меньше нуля.

Касательная и угловой коэффициент

Применение производной к исследованию функции определяется еще и касательной (прямой, направленной под углом) к графику функции в данной точке. Касательная в точке (x₀) - прямая, которая проходит через точку и принадлежит функции, координаты которой (x₀, f(x₀)), и имеющая угловой коэффициент f`(x₀).

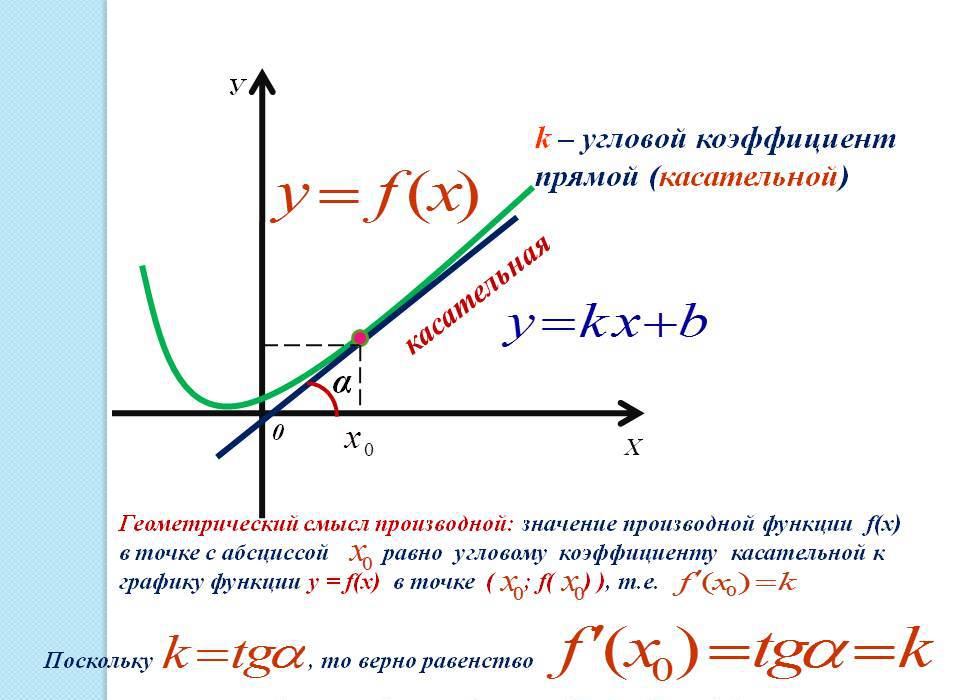
y = f(x₀) + f`(x₀)(x - x₀) - уравнение касательной к данной точке графика функции.

Геометрический смысл производной: производная функции f(x) равняется угловому коэффициенту образованной касательной к графику этой функции в данной точке x. Угловой коэффициент, в свою очередь, равняется тангенсу угла наклона касательной к оси ОХ (абсцисс) в положительном направлении. Это следствие является основополагающим к применению производной к графику функции.

Точки экстремума

Применение производной к исследованию включает в себя нахождение точек максимума и минимума.

Для того чтобы найти и определить точки минимума и максимума, необходимо:

Отыскать производную функции f(x).
Приравнять полученное уравнение к нулю.
Найти корни уравнения.
Определить точки максимума и минимума.

Чтобы найти экстремумы функции:

Отыскать точки минимума и максимума по способу выше.
Подставить эти точки в первоначальное уравнение и высчитать y_наиб. и y_наим.

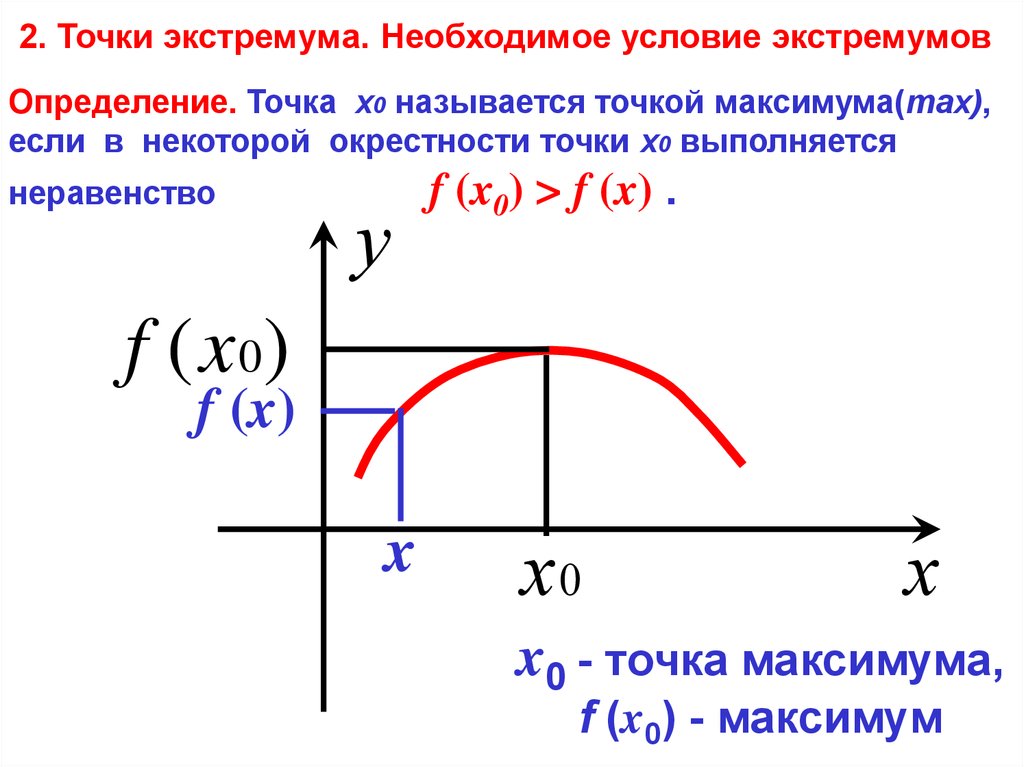
Точка максимума функции - это наибольшее значение функции f(x) на промежутке, другими словами x_наиб.

Точка минимума функции - это наименьшее значение функции f(x) на промежутке, другими словами x_наим.

Точки экстремума - то же самое, что и точки максимума и минимума, а экстремум функции (y_{наиб. и} у_наим) - значения функций, которые соответствуют точкам экстремума.

Выпуклости и вогнутости

Определить выпуклость и вогнутость можно, прибегая к применению производной для построения графиков:

Функция f(x), исследуемая на промежутке (a, b), является вогнутой, если функция расположена ниже всех своих касательных, находящихся внутри этого интервала.
Функция f(x), исследуемая на промежутке (a, b), является выпуклой, если функция расположена выше всех своих касательных, находящихся внутри этого интервала.

Точка, которая разделяет выпуклость и вогнутость, называется точкой перегиба функции.

Чтобы найти точки перегиба:

Найти критические точки второго рода (вторую производную).
Точками перегиба являются те критические точки, которые разделяют два противоположенных знака.
Вычисление значений функций в точках перегиба функции.

Частные производные

Применение производных такого типа есть в задачах, где используется больше одной неизвестной переменной. Чаще всего такие производные встречаются при построении графика функции, если быть точнее, то поверхности в пространстве, где вместо двух осей - три, следовательно, три величины (две переменные и одна постоянная).

Основное правило при вычислении частных производных - выбираем одну переменную, а остальные рассматриваем как постоянные. Следовательно, при вычислении частной производной постоянная величина становится как-будто числовым значением (во многих таблицах производных они обозначаются как C = const). Смысл такой производной - это скорость изменения функции z = f(x, y) по оси OX и OY, то есть характеризует крутизну впадин и выпуклостей построенной поверхности.

Производная в физике

Применение производной в физике имеет широкое распространение и значение. Физический смысл: производная пути по времени - скорость, а ускорение - производная скорости по времени. Из физического смысла можно провести множество ответвлений в различные разделы физики, при этом полностью сохраняя смысл производной.

С помощью применения производной находятся такие величины:

Скорость в кинематике, где вычисляется производная от пройденного пути. Если находится вторая производная от пути или первая производная от скорости, то находится ускорение тела. Помимо этого, возможно нахождение мгновенной скорости материальной точки, однако для этого необходимо знать приращение ∆t и ∆r.
В электродинамике: вычисление мгновенной силы переменного тока, а также ЭДС электромагнитной индукции. Вычисляя производную, можно найти максимальную мощность. Производная от количества электрического заряда - сила тока в проводнике.

Производная в химии и биологии

Химия: производная используется для определения скорости протекания химической реакции. Химический смысл производной: функция p = p(t), в данном случае p - количество вещества, которое вступает в химическую реакцию во времени t. ∆t - приращение времени, ∆p - приращение количества вещества. Предел отношения ∆p к ∆t, при котором ∆t стремится к нулю, называется скоростью протекания химической реакции. Среднее значение химической реакции - отношение ∆p/∆t. При определении скорости необходимо точно знать все необходимые параметры, условия, знать агрегатное состояние вещества и среду протекания. Это довольно большой аспект в химии, который широко применяется в различных отраслях и деятельности человека.

Биология: понятие производной используют при вычислении средней скорости размножения. Биологический смысл: имеем функцию y = x(t). ∆t - приращение по времени. Тогда с помощью некоторых преобразований получаем функцию y`= P(t) = x`(t) - активность жизнедеятельности популяции времени t (средняя скорость размножения). Такое применение производной позволяет вести статистику, отслеживать темпы размножения и так далее.

Производная в географии и экономике

Производная позволяет географам решать такие задачи, как нахождение численности населения, вычислять значения в сейсмографии, рассчитать радиоактивность ядерно-геофизических показателей, вычислить интерполяцию.

В экономике важную часть расчетов занимает дифференциальное исчисление и вычисление производной. В первую очередь это позволяет определить пределы необходимых экономических величин. Например, наибольшую и наименьшую производительность труда, издержки, прибыль. В основном эти величины рассчитываются по графикам функций, где находят экстремумы, определяют монотонность функции на нужном участке.

Заключение

Роль данного дифференциального исчисления задействована, как было отмечено в статье, в различных научных структурах. Применение производных функций - важный элемент в практической части науки и производства. Не зря нас в старшей школе и университете учили строить сложные графики, исследовать и работать над функциями. Как видим, без производных и дифференциальных исчислений невозможно было бы рассчитать жизненно важные показатели и величины. Человечество научилось моделировать различные процессы и исследовать их, решать сложные математические задачи. Действительно, математика - царица всех наук, потому что эта наука лежит в основе всех других естественных и технических дисциплин.

В процессе изучения производной в школьном курсе математики рассматриваются некоторые её приложения в физике, а также ряд текстовых задач на нахождение наибольшего или наименьшего значений. Однако сфера производной применения этим не ограничивается. Например, существует масса реальных экономических задач, для решения которых необходимо использовать методы дифференциального исчисления.

Метод нахождения экстремальных значений функции имеет важнейшее, ключевое значение для решения большого класса задач из разных разделов курса физики, математики, экономики и других наук. Специфика этих задач включает получение на основе некоторых физических и математических закономерностей функциональной зависимости и нахождение экстремального значения. В наше время, в связи с научно-техническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становится все более актуальным в решении как простых, так и сверхсложных задач.

Цель: исследовать применение производной в различных областях науки и техники.

Задачи: 1)рассмотреть применение производной в практической деятельности;2) подбор физических и экономических задачи на экстремум; 3) показать применение производной к выяснению истинности неравенств.

Методы исследования: анализ и решение, сравнение результатов с реальной действительностью.

Каждый человек время от времени оказывается в ситуации, когда надо отыскать наилучший способ решения какой-либо задачи, и математика становится средством решения проблем организации производства, поисков оптимальных решений. Важным условием повышения эффективности производства и улучшения качества продукции является широкое внедрение математических методов в технику. Среди задач математики большую роль отводят задачам на экстремумы, т.е. задачам на отыскание наибольшего и наименьшего значения, наилучшего, наиболее выгодного, наиболее экономного. С такими задачами приходиться иметь дело представителям самых разных специальностей: инженеры-технологи стараются так организовать производство, чтобы получилось как можно больше продукции, конструкторы хотят так спланировать прибор на космическом корабле, чтобы масса прибора была наименьшей, экономисты стараются спланировать прикрепление заводов к источникам сырья так, чтобы транспортные расходы оказывались минимальными.

ГЛАВА I. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ

§1. Геодезия

Если расстояние между точками B и C достаточно велико, то к найденному (с помощью угломерных инструментов) значению повышения точки B над точкой C прибавляют так называемую поправку на кривизну Земли: , где R – радиус Земли, l – длина горизонтальной проекции отрезка BC.

Докажем указанную выше формулу для поправки . Рассмотрим рис. 1, на котором штрихами изображена поверхность океана, точка O – центр Земли. Пусть точка C лежит на поверхности океана, а точка B принадлежит горизонтальной плоскости, проходящей через точку C. Так как в таком случае угол между лучом CB и горизонтальным направлением (оно определяется с помощью отвеса) равен нулю, то из точки C нам покажется, что точки B и C имеют одинаковую высоту. Согласившись с этим, мы допустим погрешность .

§2. Транспорт

В практике проектирования сети автомобильных дорог часто возникает необходимость устройства узла разветвления. Местоположение узла и взаимное расположение проходящих через него дорог определяется комплексом экономических и географических условий, но первый, предварительный этап решение этой задачи учитывает лишь затраты рабочего времени на перевозки, причём в качестве вспомогательной решается вначале следующая задача.

Каким должен быть угол примыкания (рис. 2) дороги (CE) к автомагистрали (AB), чтобы затраты времени на перевозки по маршруту AEC были наименьшими, если скорость движения автомобилей по магистрали планируется равной, а по объездной дороге – ()? Проведем через точку C перпендикуляр к прямой AB и обозначим длину отрезка CD через h, а длину отрезка AD через l. Тогда получим: , . Отсюда находим время движения автомобиля по маршруту AEC: . Так как точка A зафиксирована условно, определяя лишь направление движение по магистрали, то может изменяться в промежутке . Задача свелась к отысканию наименьшего значения в промежутке значения функции на указанном промежутке.

Найдём производную . Так как , то производная на рассматриваемом промежутке обращается в нуль лишь в одной точке , причём при и при . Это означает, что на промежутке функция t убывает, а на промежутке возрастает. Следовательно, рассматриваемая функция t при достигает наименьшего значения.

§3. Мелиорация

Площадь поперечного сечения канала называют его живым сечением, а длину границы такого сечения называют смоченным периметром канала. С помощью теоретических расчетов и эксперимента установлено, что из всех каналов с заданным живым сечением наибольшей пропускной способностью и одновременно наименьшей фильтрацией отличаются каналы с наименьшим смоченным периметром. Про такие каналы говорят, что они имеют гидравлически наивыгоднейший профиль.

В мелиоративной практике часто сооружаются каналы или лотки с поперечным сечением в форме прямоугольника, треугольника, трапеции и сегмента круга. Поэтому представляет интерес расчет гидравлически наивыгоднейшого профиля для каналов такой формы.

При каком отношении глубины к ширине канал прямоугольного сечения имеет гидравлически наивыгоднейший профиль? Пусть x – ширина канала, – его живое сечение. Тогда глубина канала , а его смоченный периметр (рис. 3): .

Требуется найти наименьшее значение функции на промежутке . Найдем производную: . Так как , при и при , то функция в точке достигает наименьшего значения.

Итак, ширина канала в рассматриваемом случае должна быть , глубина , а искомое отношение равно 0,5.

Сечение канала – равнобедренная трапеция (рис. 4) с углом откоса таким, что . При каком отношении ширины дна канала к его глубине он имеет гидравлически наивыгоднейший профиль? Пусть ширина дна канала b, а его глубина h. Тогда , , (1), . Из (1) получаем, что , а значит (0 2, то .

Решение. Рассмотрим функцию . Найдем ее производную: .

Отсюда видно, что при x > 2 имеем , т.е. .

Итак, проверяемое утверждение справедливо.

Пример 3. Известно, что если числа и заключены между 0 и и , то . Верно ли неравенство ?

Решение. Рассмотрим вспомогательную функцию . Имеем при . Следовательно, на возрастает, и поэтому при , т.е. проверяемое неравенство верно.

Пример 4. Пусть p и q – положительные числа, . Тогда, очевидно, , . Можно ли гарантировать, что неравенство верно а) при ; б) при ?

Решение. а) Рассмотрим функцию . Имеем: . Отсюда видно, что при функция возрастает. В частности, она возрастает на интервале . Поэтому при проверяемое неравенство справедливо.

б) На интервале , т.е. убывает. Поэтому при любых p и q, для которых , проверяемое неравенство неверно, а верно неравенство противоположного смысла .

§2. От числовых неравенств – к функциональным

Пример 5. Что больше: или ; или ; или ; или ; или ?

Решение. Все эти задачи сводятся к такой вспомогательной функциональной задаче.

Если , то при каких условиях верно неравенство (1), а при каких условиях верно неравенство ? Неравенство (1) равносильно таким неравенствам: , .

Рассмотрим вспомогательную функцию (2) и выясним, в каком промежутке она будет возрастать. Имеем . Понятно, что при и при . Поэтому функция (2) возрастает на и убывает на . Иными словами, если , то , ; если же , то , . Значит, , но , , , .

§3. Неравенства с несколькими переменными

Пример 6. Выяснить, что больше при : или . Решение. Нам предстоит сравнить с числом 1 дробь . Рассмотрим на вспомогательную функцию . Выясним, будет ли она монотонна на отрезке . Для этого найдем ее производную. После упрощений получим: при . В силу теоремы 1 функция возрастает на отрезке . Поэтому при , т.е. , при .

Пример 7. Проверить, справедливо ли при любых положительных a, b, c неравенство (3).

Решение. Пусть . Рассмотрим функцию . При имеем . Отсюда видно, что убывает на . Поэтому при имеем , т.е. мы получили неравенство (4). Теперь рассмотрим другую вспомогательную функцию . При имеем: . Следовательно, убывает на , т.е. при , значит, (5). Из (4) и (5) следует (3).

Примечание. Обратим внимание на то, что из (3) следует: при любом выборе положительных чисел x, y, z . Для доказательства достаточно заметить, что можно считать и что можно подобрать числа a, b, c так, чтобы , , ; затем привлекаем (3).

Для выяснения истинности неравенства иногда удобно воспользоваться следующим утверждением, которое непосредственно вытекает из теоремы 1:

Теорема 2. Пусть функция непрерывна на и пусть имеется такая точка c из , что на и на . Тогда при любом x из справедливо неравенство , причем равенство имеет место лишь при .

Пример 8. Проверьте, справедливо ли для всех действительных x следующее неравенство: .

Решение. Выясним, где функция возрастает, а где убывает. Для этого найдем производную . Отсюда видно, что на и на . Следовательно, в силу теоремы 2 , т.е. справедливо проверяемое неравенство, причем равенство имеет место лишь .

Пример 9. Пусть a, b, p, q – положительные числа и (6). Проверить справедливость неравенства .

Решение. Данное неравенство равносильно такому , т.е. (7).

Рассмотрим на вспомогательную функцию и выясним, где она возрастает, а где убывает. . В силу (6) имеем , и поэтому . Отсюда имеем, что при и при . Поэтому функция на убывает, а на возрастает. Следовательно, на функция принимает свое наименьшее значение при . Поэтому , причем равенство возможно лишь при , т.е. .

Учитывая (6), нетрудно посчитать, что , следовательно, справедливо неравенство (7), а значит, и проверяемое неравенство.

§4. Доказательство неравенств Гюйгенса

Для нахождения приближенных значений числа геометры со времен Архимеда до середины XVII века пользовались неравенствами (8), где C – длина окружности, и - периметры правильных n-угольников, соответственно вписанного в эту окружность и описанного около нее.

Пусть R – радиус окружности. Тогда , , ; неравенства (10) принимают вид (если положить ради краткости ): . Или после упрощений: (11). Мы докажем, что неравенства (11) верны для всех чисел из (а не только для чисел вида ). После элементарных преобразований видим, что нам предстоит доказать следующие два неравенства (при ): (12), (13).

Доказательство неравенства (12). Рассмотрим на функцию (14). Найдем на : . Следовательно, убывает на , так что при имеем , т.е. (15).

Доказательство неравенства (13). Рассмотрим на функцию . Если покажем, что на возрастает, то получим, в частности, при , т.е. (13) будет доказано.

Вычислим и выясним, будет ли на . . После элементарных упрощений находим (см. (14)) , где определяется формулой (14). Так как при (см. (15)), то при , т.е. возрастает на . Поэтому при . Но это означает, что неравенство (13) справедливо.

Заключение

Математика служит основой естественных и технических наук, без нее ныне не мыслима ни одна современная технология. Кроме того, математика активно внедряется в экономику. Приступая к данному исследованию, мы ставили перед собой задачу: применение производной на нахождение экстремальных значений функции в различных областях практической деятельности. Для этого:

были выбраны задачи из сборников задач по физике и подготовке к единому государственному экзамену, в которых требовалось найти наименьшее или наибольшее значение;

выполнено решение подобранных задач;

выполнена классификация задач по разделам физики, математики и экономики.

Применение производной довольно широко и его сложно полностью охватить в работе такого типа, однако, мы попытались раскрыть основные, базовые моменты. В наше время, в связи с научно-техническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становится все более актуальным в решении как простых, так и сверхсложных задач. Можно сказать, что задачи на отыскание наименьшего и наибольшего значения, имеют большое практическое применение. В данной работе показано решение таких задач.

Литература

Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Федорова Н.Е., Шабунин М.И. Алгебра и начала анализа 10-11 классы, М., Просвещение, 2003.

Москалев А.Н., Никулова Г.А. Готовимся к единому государственному экзамену. Физика. М., Дрофа, 2007.

Цель: исследовать применение производной в различных областях науки и техники.

Методы исследования: анализ и решение, сравнение результатов с реальной действительностью.

ГЛАВА I. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ

§1. Геодезия

§2. Транспорт

§3. Мелиорация

Итак, ширина канала в рассматриваемом случае должна быть , глубина , а искомое отношение равно 0,5.

Решение. Рассмотрим функцию . Найдем ее производную: .

Отсюда видно, что при x > 2 имеем , т.е. .

Итак, проверяемое утверждение справедливо.

Пример 3. Известно, что если числа и заключены между 0 и и , то . Верно ли неравенство ?

§2. От числовых неравенств – к функциональным

Пример 5. Что больше: или ; или ; или ; или ; или ?

Решение. Все эти задачи сводятся к такой вспомогательной функциональной задаче.

§3. Неравенства с несколькими переменными

Пример 7. Проверить, справедливо ли при любых положительных a, b, c неравенство (3).

Пример 8. Проверьте, справедливо ли для всех действительных x следующее неравенство: .

Пример 9. Пусть a, b, p, q – положительные числа и (6). Проверить справедливость неравенства .

Решение. Данное неравенство равносильно такому , т.е. (7).

§4. Доказательство неравенств Гюйгенса

Заключение

выполнено решение подобранных задач;

выполнена классификация задач по разделам физики, математики и экономики.

Литература

Москалев А.Н., Никулова Г.А. Готовимся к единому государственному экзамену. Физика. М., Дрофа, 2007.

Читайте также: