Площадь треугольника доказательство 8 класс кратко

Обновлено: 21.05.2024

Формула для площади треугольника и следствия из неё

На данном уроке мы докажем формулу для площади треугольника и решим несколько задач на её применение.

Будем называть сторону – основанием, тогда – высота, опущенная к этой стороне (см. Рис. 1).

Рис. 1. Высота и основание

Теорема о свойстве медианы треугольника

Площадь треугольника равна половине произведения его основания на высоту.

В формульном виде: .

Доказательство:

Рис. 2. Иллюстрация к теореме

Достроим треугольник до параллелограмма – см. Рис. 2.

(по трём сторонам: – общая, , – как противоположные стороны параллелограмма).

Из равенства треугольников следует равенство их площадей: . Получаем: . Воспользовавшись формулой для площади параллелограмма: .

Сформулируем несколько следствий из данной теоремы.

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов (см. Рис. 3).

Рис. 3. Иллюстрация к следствию 1

Следствие 2

Если высоты двух треугольников равны, то их площади относятся как основания (см. Рис. 4).

Рис. 4. Иллюстрация к следствию 2

Теорема 2

Медиана треугольника разбивает его на два равновеликих треугольника (см. Рис. 5).

Доказательство:

Рис. 5. Иллюстрация к теореме

Пусть – треугольник, – медиана, – высота. Для треугольников – также является высотой. Запишем формулу для площади каждого из этих треугольников: , . Так как ( – медиана), то: . Значит, эти треугольники являются равновеликими.

Формула для площади ромба

Теорема 3

Площадь ромба равна половине произведения его диагоналей (см. Рис. 6).

В виде формулы: .

Доказательство:

Рис. 6. Иллюстрация к теореме

(по 3 сторонам: – общая, – свойства ромба). Из равенства треугольников следует равенство их площадей. Значит: . Но формулу для площади треугольника мы уже знаем: (т. к. , поэтому – высота треугольника ). Получаем следующее равенство: ( – свойство диагоналей ромба).

Свойство треугольников с равными углами

Теорема 4

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

В виде формулы: .

Доказательство:

Рис. 7. Иллюстрация к теореме

Совместим треугольники так, чтобы вершина совпала с вершиной , сторона лежала на прямой , а сторона лежала на прямой .

Рис. 8. Иллюстрация к теореме

Рассмотрим отношение площадей треугольников и . Эти треугольники имеют общую высоту, проведённую из вершины , поэтому, по следствию 2 из теоремы 1, их площади относятся как основания, то есть: .

Из аналогичных соображений: . Перемножив эти два равенства, получим: .

Задачи на площадь треугольника и следствия из неё

Теперь решим несколько задач, используя доказанные формулы и свойства.

Задача 1

Площадь прямоугольного треугольника равна . Найдите катеты этого треугольника, если известно, что один из них составляет другого.

Решение

Пусть один из катетов равен , а второй – . Тогда площадь треугольника можно вычислить по формуле: . Но, по условию: . Подставив это выражение, получаем: . Откуда: .

Ответ: .

Задача 2

В треугольнике точка лежит на стороне , точка лежит на стороне . Кроме того: , , . Чему равна площадь треугольника (Рис. 9)?

Решение:

Рис. 9. Иллюстрация к задаче

Воспользуемся теоремой 4 для треугольников и ( – общий угол этих треугольников). Из этой теоремы следует, что: . Значит: .

Ответ: .

На этом уроке мы рассмотрели понятия площадей треугольника и ромба, вывели из них некоторые следствия. На следующем уроке мы научимся вычислять площадь трапеции.

В этом уроке мы введем формулу площади для произвольного треугольника. Докажем ее. Убедимся, что площадь прямоугольного треугольника равна половине произведения длин его катетов. А также научимся применять эти формулы при решении практических задач.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Площадь треугольника"

Прежде, чем рассматривать вопрос о нахождении площади треугольника, вспомним, что высотой треугольника называется перпендикуляр, проведённый из вершины треугольника на противоположную сторону или её продолжение.

Теперь докажем, что площадь треугольника равна половине произведения длины стороны на высоту, проведённую к ней.

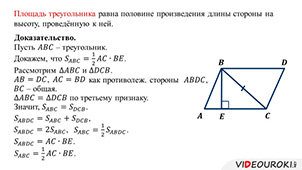
Доказательство

Пусть – треугольник.

Докажем, что .

Рассмотрим и .

,как противолеж. стороны ,

– общая.

по третьему признаку.

Значит, .

Что и требовалось доказать.

Из доказанного следует, что площадь прямоугольного треугольника равна половине произведения длин его катетов.

Возьмём некоторый прямоугольный треугольник ABC. Катет AC – это и есть высота, проведённая к стороне BC, которая также является катетом.

А тогда, так как площадь треугольника равна половине произведения длины стороны на высоту, проведённую к ней, получаем, что площадь треугольника
, то есть равняется половине произведения длин катетов рассматриваемого треугольника.

Также следует, что если высота одного треугольника равна высоте другого треугольника, то их площади относятся как длины сторон, к которым проведены высоты.

На рисунке перпендикуляр BE, проведённый к прямой AC, является высотой треугольника ABC и треугольника CBD.

, то есть как длины сторон треугольников, к которым проведены высоты.

Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Доказательство.

Рассмотрим треугольники ABC и A₁B₁C₁. Пусть S – площадь треугольника ABC, а S₁ – площадь треугольника A₁B₁C₁. Углы А и A₁ этих треугольников равны.

– площадь ,

– площадь .

Докажем, что .

Таким образом, теорема доказана.

Закрепим новый материал на практике.

Задача. Найдите площадь треугольника , если длина стороны см, а высота , проведённая к этой стороне, в два раза её меньше.

(см).

(см 2 ).

Ответ: см 2 .

Задача. Вычислите площадь треугольника , если высота см, отрезок см, а .Решение.

– прямоугольный,

так как – высота.

тогда .

Значит, – равнобедренный, тогда см.

(см).

(см 2 ).

Ответ: см 2 .

Задача. Найдите длины катетов прямоугольного треугольника, если они относятся как , а его площадь равна см 2 .

, (см).

(см).

Ответ: см, см.

Итак, на этом уроке мы доказали, что площадь треугольника равна половине произведения длины стороны на высоту, проведённую к ней.

Убедились, что площадь прямоугольного треугольника равна половине произведения длин его катетов. А также, что если высота одного треугольника равна высоте другого треугольника, то их площади относятся как длины сторон, к которым проведены высоты.

Доказали теорему: если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Формулы, позволяющие находить площадь треугольника , удобно представить в виде следующей таблицы.

a – любая сторона,
h_a – высота, опущенная на эту сторону

a и b – две любые стороны,
С – угол между ними

a – любая сторона,
B, С – прилежащие к ней углы

a – катет,
φ – прилежащий острый угол

a – катет,
φ – противолежащий острый угол

c – гипотенуза,
φ – любой из острых углов

где
a – любая сторона,
h_a – высота, опущенная на эту сторону

где
a и b – две любые стороны,
С – угол между ними

где
a – любая сторона,
B, С – прилежащие к ней углы

где
a – катет,
φ – прилежащий острый угол

где
a – катет,
φ – противолежащий острый угол

где
c – гипотенуза,
φ – любой из острых углов

Произвольный треугольник

где
a – любая сторона,
h_a – высота, опущенная на эту сторону

где
a и b – две любые стороны,
С – угол между ними

где
a – любая сторона,
B, С – прилежащие к ней углы

где
a – катет,
φ – прилежащий острый угол

где
a – катет,
φ – противолежащий острый угол

где
c – гипотенуза,
φ – любой из острых углов

Вывод формул для площади произвольного треугольника

Утверждение 1 . Площадь треугольника можно найти по формуле

где a – любая сторона треугольника, а h_a – высота, опущенная на эту сторону.

что и требовалось доказать.

Утверждение 2 . Площадь треугольника можно найти по формуле

где a и b – две любые стороны треугольника, а С – угол между ними.

то, в силу утверждения 1, справедлива формула

что и требовалось доказать.

Утверждение 3 . Площадь треугольника можно найти по формуле

где a – любая сторона треугольника, а B, С – прилежащие к ней углы.

Замечание . Докажем утверждение 3 в случае остроугольного треугольника. Доказательство в случаях прямоугольного и тупоугольного треугольников требует лишь незначительных изменений, совершить которые мы предоставляем читателю в качестве самостоятельного упражнения.

что и требовалось доказать.

Утверждение 4 . Площадь треугольника можно найти по формуле

где a, b, c – стороны треугольника, а r – радиус вписанной окружности.

Соединив центр O вписанной окружности с вершинами треугольника (рис.4), получим

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Вывод формулы с доказательством

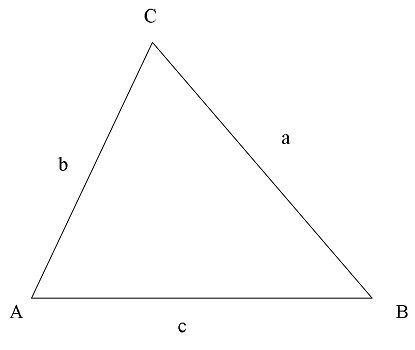
Для доказательства теоремы возьмем произвольный треугольник ABC.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Пусть BC = a, CA = b, S — площадь треугольника ABC.

Докажем, что \(S=\frac12ab\cdot\sin C\)

Введем координатную плоскость и впишем в нее треугольник ABC так, чтобы:

точка C совпадала с началом координат;
точка B лежала на положительной оси Cx;
точка A находилась в верхней полуплоскости.

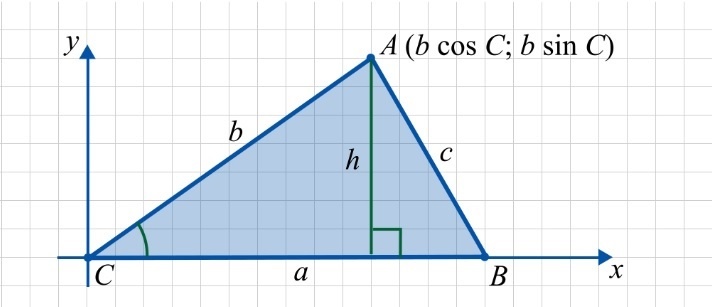
С учетом описанных условий вычисление площади треугольника можно произвести по формуле:

где h — высота треугольника. В данном случае h равна ординате точки A.

Получается, что \(h=b\cdot\sin C.\)

Это связано с тем, что \(\sin C\) равен отношению противолежащего катета (то есть h) к гипотенузе (то есть к b):

Отсюда выражаем h и получаем:

Как следствие \(S=\frac12ab\cdot\sin C\) , то есть вместо \(h\) подставляем \(b\cdot\sin C\) . Теорема геометрии доказана.

Пример решения задачи

Задача

Дан прямоугольный треугольник \(ABC\) , где \(AB = 3\) , \(AC = 4\) , \(\angle A=30\) .

Найти площадь треугольника.

Решение

Для того чтобы найти площадь треугольника, воспользуемся ранее доказанной теоремой.

В формулу \(S=\frac12AB\cdot AC\cdot\sin A\) подставляем записанные выше исходные показатели и производим расчет.

Читайте также: