Оптимизация логических схем лекция кратко

Обновлено: 02.07.2024

Аннотация: Рассматривается взаимосвязь различных способов описания работы логических схем и принципы их минимизации.

Составление логических выражений по таблице истинности

Каноническая сумма минтермов

Минтерм - это полное произведение всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно логической 1. Переменная входит в минтерм с инверсией, если ее значение в данной строке таблицы равно 0, и без инверсии, если ее значение в данной строке таблицы равно 1.

Каноническая сумма минтермов - это логическая сумма всех минтермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности.Она составляется в следующей последовательности:

В заданной таблице истинности подсчитывается - количество строк таблицы, в которой значение функции равно 1.
Затем записывается логическая сумма полных произведений.
Далее в каждом произведении расставляются инверсии над переменными в соответствии с их значением в строке таблицы.

Для примера, представленного на рис. 1.6, каноническая сумма минтермов будет выглядеть так:

$f = \overline\overlinecd+ \overlineb\overlined + \overlinebcd + ab\overlined+abcd.$

( 2.1)

Из сравнения (1.1) и (2.1) видно, что одной и той же таблице истинности (рис. 1.6,б) соответствуют два разных логических выражения, причем (1.1) записывается более компактно, но возможности минимизации для него еще есть. Следовательно, есть возможность минимизировать и логическую схему, представленную на рис. 1.6, a.

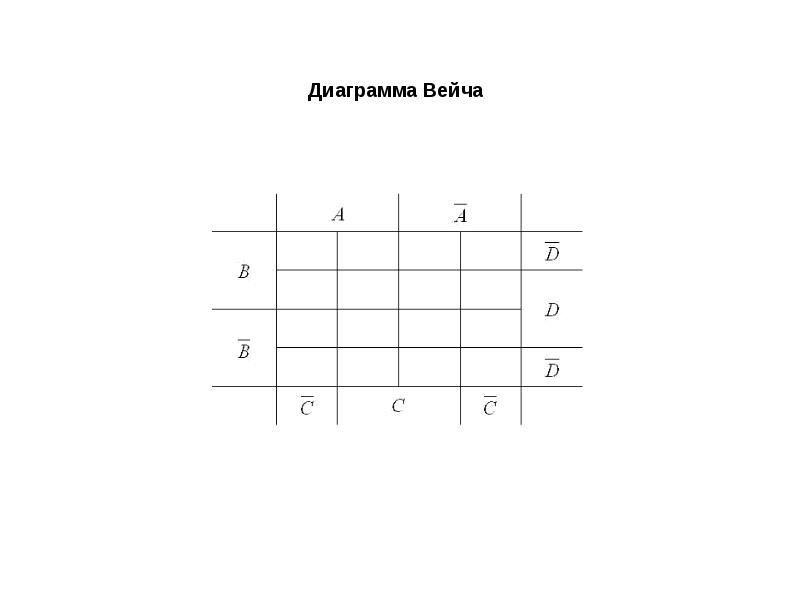
Минимизация логических выражений может осуществляться с помощью различных методов на основе правил булевой алгебры, в частности, диаграммы Вейча , диаграммы Венна и табличным методом, но наиболее простым и наглядным является графический способ минимизации с помощью карт Карно, опубликованный в 1953 г. Морисом Карно.

Минимизация с помощью карт Карно

Карта Карно - графическое представление таблицы истинности. Каждой клетке карты Карно соответствует строка таблицы истинности. По осям карты расставляются сочетания переменных, а внутри карты - значения функции.

Назначение карты Карно - найти логические суммы прямого и инверсного значения переменных. Для любой переменной, например, , такая сумма равна при любом значении : при это будет , при это . Поэтому при вынесении за скобки в выражении:

$abc + \overlinebc = bc (a + \overline ) = bc\cdot 1=bc$

$а + \overline= 1$

- сумму можно отбросить, при этом результат выражения не изменится. В этом и заключается минимизация логических выражений с помощью карт Карно. Для достижения поставленной цели минимизации нужно соблюдать правила разметки осей карты:

Вертикальная ось размечается независимо от горизонтальной.
Начинать разметку можно с любого сочетания переменных.
Все сочетания переменных должны быть перечислены.
Для соседних клеток карты сочетание переменных должно отличаться не более чем одним знаком, причем соседними являются крайние клетки строки (столбца).

Для функции двух переменных карта Карно - это квадрат 2x2 клетки. В этих клетках размещаются 4 значения функции из последнего столбца таблицы истинности (рис. 2.2).

Для функции трех переменных карта Карно - это прямоугольник 2x4 или 4x2 клетки. В этих клетках размещаются 8 значений функции из последнего столбца таблицы истинности (рис. 2.3). При разметке большей из осей нужно четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы соседними не оказались сочетания и , либо и , в которых одновременно меняются обе переменные.

Для функции четырех переменных карта Карно - это квадрат 4x4 клетки. В этих клетках размещаются 16 значений функции из последнего столбца таблицы истинности (рис. 2.4). При разметке обеих осей нужно также четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы по одной оси соседними не оказались сочетания и , либо и , в которых одновременно меняются обе переменные.

Для функции пяти переменных карта Карно представляет собой уже объемную фигуру - куб 4x4x4 клетки, поэтому для минимизации логических выражений она не применяется.

увеличить изображение
Рис. 2.3. Таблица истинности (а) и примеры заполнения карты Карно (б, в, г, д) для логической функции 3 переменных.

увеличить изображение
Рис. 2.4. Таблица истинности (а) и примеры заполнения карты Карно (б, в) для логической функции 4 переменных.

В конкретных случаях вместо значений функций в общем виде в клетки карты проставляются конкретные значения (логические 0 и 1) из соответствующих строк таблицы истинности. Затем рассматриваются только те клетки, которые заполнены единицами. Все эти единицы должны быть обведены контурами по следующим правилам составления контуров:

Контуры должны быть прямоугольными и содержать количество единиц, равное , где - целое число. Таким образом, в контуре может быть либо одна, либо две, либо четыре, либо восемь единиц.
Количество единиц в контуре должно быть максимальным, при этом контуры могут пересекаться между собой. Нужно учитывать, что крайние строки являются соседними и крайние столбцы также являются соседними, поэтому контуры могут быть "разорванными".
Количество контуров должно быть минимальным, но все единицы должны быть охвачены контурами. Нельзя забывать об отдельно стоящих единицах. Каждая такая единица - это контур, которому соответствует полное логическое произведение всех переменных.

После обведения контуров нужно записать минимальное выражение как логическую сумму логических произведений. Каждому произведению соответствует один контур карты Карно. В произведение входят только те переменные, которые остаются в данном контуре неизменными.При этом переменная входит в произведение с инверсией, если ее значение в данном контуре равно 0, и без инверсии, если ее значение равно 1.

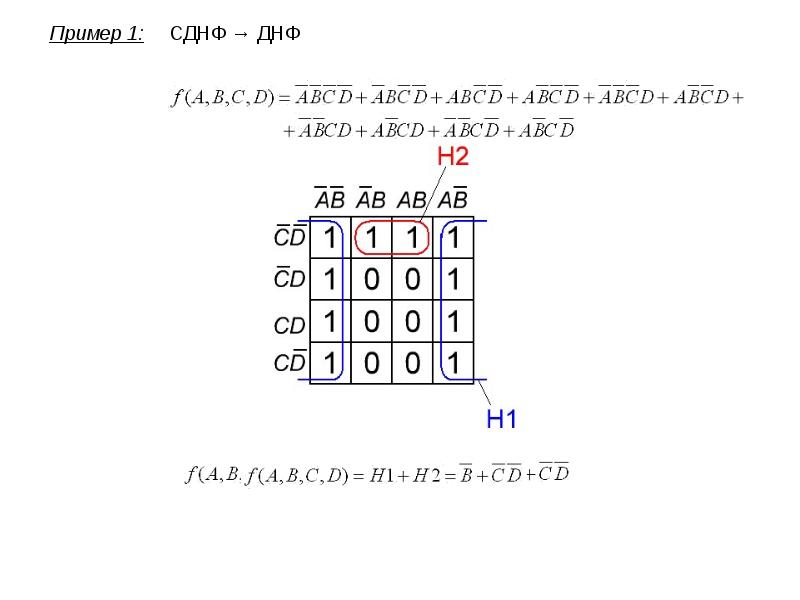
Пример 1. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.5,а и нарисовать по нему логическую схему.

При одном варианте разметки осей (рис. 2.5,б) первый контур, состоящий из четырех единиц, получается разорванным. Если же принять разметку, показанную на рис. 2.5,в, то контур будет иметь нормальные очертания, а выражение, ему соответствующее, останется без изменений. Учитывая, что при данном горизонтальном начертании карты Карно крайние столбцы являются соседними, ее можно представить себе как цилиндр, развернутый на плоскости. На рис. 2.5,б представлена развертка такого цилиндра, "разрезанная" между комбинациями , равными и . А на рис. 2.5,в представлена развертка этого же цилиндра, "разрезанная" между произведениями , равными и .

Первый контур охватывает четыре единицы, ему соответствует сумма минтермов: +abc+ab\overline" />
, в которой не изменяется только переменная . Второй контур охватывает две единицы. Ему соответствует сумма минтермов +a\overline\overline" />
, в которой переменная принимает оба возможных значения, а произведение " />
остается неизменным. Таким образом, получаем минимальное выражение:

$f= b + a\overline<c>.$

( 2.2)

Ему соответствует логическая схема на рис. 2.5,г.

Для сравнения запишем максимальное выражение:

$f= \overlineb \overline+ \overlinebc+ a\overline\overline+ab\overline+abc.$

( 2.3)

Разница между (2.2) и (2.3) очевидна и в комментариях не нуждается, за исключением того, что схема, реализованная по (2.3), будет на порядок сложнее и, соответственно, менее надежна, чем схема, показанная на рис. 2.5,г.

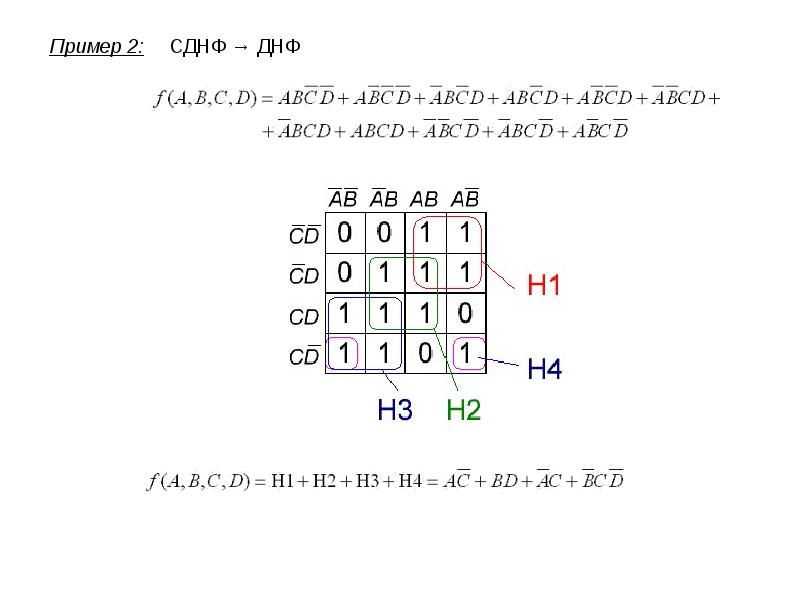
Пример 2. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.6,а, и нарисовать по нему логическую схему.

При первоначально выбранной разметке осей (рис. 2.6,б) первый контур, состоящий из четырех единиц с номерами 1.1, 1.2, 1.3 и 1.4, расположенных по углам карты, получается разорванным. Если же принять разметку, показанную на рис. 2.7, то контур будет иметь очертания квадрата, а выражение, ему соответствующее, останется без изменений. Учитывая, что крайние столбцы являются соседними и крайние строки являются соседними, карту Карно для функции четырех переменных можно представить себе как торроид, развернутый на плоскости. Проще представить себе обратный процесс получения торроида из плоской фигуры - квадрата. Для этого надо сначала соединить мысленно крайние строки - получим цилиндр. После этого основания цилиндров надо мысленно соединить. Получится торроид. На рис. 2.6,б представлена развертка такого торроида, "разрезанная" между комбинациями , равными и и между сочетаниями , равными и . А на рис. 2.7 представлена развертка этого же торроида, "разрезанная" между комбинациями , равными и и между произведениями , равными и . После анализа контуров получим минимальное выражение +c\overline+a\overlined+\overline\overlined" />
. Соответствующая ему схема приведена на рис. 2.8.

1) Реализация функций с помощью однотипных микросхем.

или-не

и-не

Схемы из крупных блоков часто бывают более простыми. Недостаток - избыточность аппаратной части.

2) Программируемые логические матрицы.

Универсальные логические блоки. Мультиплексор.

Универсальные логические блокиявляются шаблоном, их можно настроить под конкретные задачи.

Mультиплексор — устройство, имеющее несколько сигнальных входов, один или более управляющих входов и один выход. Мультиплексор позволяет передавать сигнал с одного из входов на выход; при этом выбор желаемого входа осуществляется подачей соответствующей комбинации управляющих сигналов.

Сигналы на адресных входах определяют, какой конкретно информационный канал подключен к выходу. Если между числом информационных выходов и числом адресных входов действует соотношение , то такой мультиплексор называют полным. Если , то мультиплексор называют неполным.

Обобщённая схема мультиплексора

Кроме этого, некоторые мультиплексоры могут иметь выход с тремя состояниями: два логических состояния 0 и 1, и третье состояние — отключённый выход (высокоимпедансное состояние, Z-состояние — выходное сопротивление равно бесконечности). Перевод мультиплексора в третье состояние производится снятием управляющего сигнала OE (от англ. Output Enable).

Универсальные логические блоки. ПЛМ.

Универсальные логические блокиявляются шаблоном, их можно настроить под конкретные задачи.

Структура ПЛМ

ПЛМ представляет собой функциональный блок, созданный на базе полупроводниковой технологии и предназначенных для реализации логических функций цифровых систем.

Использование ПЛМ объясняется рядом причин:

- в связи с уважением программного обеспечения наметилась тенденция выполнять многие функции современных ЭВМ аппаратным способом;

- в интегральной технологии созданы новые схемотехнические решения, благодаря которым резко увеличивалась информационная ёмкость ПЛМ;

- созданы методы автоматизированного проектирования ПЛМ с использованием ЭВМ;

- значительно расширилась область использования ПЛМ в устройстве различного назначения;

ПЛМ подразделяются на два типа в зависимости от внутренней организации:

1. ПЛМ комбинационной логики

2. ПЛМ с памятью.

ПЛМ комбинационной логики состоит из двух матриц М₁ иМ₂ (рис. а)

Первая матрица формирует q термов, зависящих от S переменных. Вторая матрица формирует t дизъюнкций от терминов, полученных в матрице М₁. ПЛМ комбинационной логики определяется параметрами (s, t, g). Любая система булевых функций от переменных , дизъюнктивная нормальная форма которых содержит Н терминов может быть реализована на одной ПЛМ. Условное обозначение ПЛМ приведено на рис. b.

ПЛМ с памятью содержат регистр RF, содержащий r разрядов (рис. а) в цепи обратной связи между матрицами М₁ иМ₂ число r элементов памяти выбирается так, чтобы удовлетворялось неравенство . ПЛМ с памятью характеризуется параметрами (s, t, q ,r) Любой управляющий автомат с входными, выходными переменными (микрооперациями и числами переходов может быть тривиальным образом реализован на одном ПЛМ.

Программирование ПЛМ

В зависимости от способа программирования, т. е. от способа организации межсоединений шин в матрицах, различают два типа ПЛМ:

1. ПЛМ программируемые в процессе изготовления. В ПЛМ этого типа межсоединений шин в матрицах осуществляется на последнем этапе процесса изготовления с помощью маски и в дальнейшем изменены быть не могут. Такой способ называется масочным программированием.

2. ПЛМ, программируемые пользователем. ПЛМ этого типа поставляются потребителю незапрограммированными. Программирование осуществляется электрическим способом при помощи специального оборудования (программатора и т. п.) Наибольшее распространение получил способ программирования, основанный на устранении ненужных межсоединений шин в матрицах, путём пережигания перемычек под действием тока повышенной амплитуды. Кроме того, существуют ПЛМ, программирование которых основано на пробое перехода транзисторов.

3. Репрограммируемые ПЛМ.

Такие ПЛМ позволяют осуществлять программирование неоднократно. Повторное программирование выполняется электрическим способом после стирания содержимого ПЛМ под действием ультрафиолетового (иногда рентгеновского) облучения электрическим способом отдельно для каждого межсоединения шин в матрицах.

Приведение выражения к каноническому виду с последующем
упрощением
1. Выражение записанное в дизъюнктивной форме можно привести к СДНФ
путём умножения импликат на множитель типа
2.После
раскрытия
скобок,
члены
выражения
могут
быть
перегруппированы, что в результате получится упрощенное выражение.
так
Порядок
выполнения
операций:
сначала
выполняются
операции
конъюнкций, а затем дизъюнкций. В сложных логических выражениях
для задания порядка выполнения используют скобки.
При необходимости для формирования групп можно ввести повторяющиеся
члены.
Пример:

Минимизация с помощью карт Карно
Правила разметки:
Вертикальная ось размечается независимо от горизонтальной.
Начинать разметку можно с любого сочетания переменных.
Все сочетания переменных должны быть перечислены.
Для соседних клеток сочетания переменных должны отличаться не более
чем одним знаком.
Соседними являются крайние клетки строки или столбца.

Правила составления контуров
Контуры должны быть прямоугольными и содержать количество единиц,
равное 2n, где n – целое число, т.е. в контуре может быть 1, 2, 4, 8. и т. д.
единиц.
Количество единиц в контуре должно быть максимальным, при этом
контуры могут пересекаться между собой.
Количество контуров должно быть минимальным, но все единицы
должны быть охвачены контурами.

13. Построение логических схем

Этап IV. Минимизировать СДНФ любым доступным методом.
Этап V. Реализовать получившиеся дизъюнктивные формы на логическом
базисе заданного семейства элементов.
Этап VI. Оценить двойственный вариант логической схемы с учётом
изменения числа входных и выходных инверторов.
Этап VII. Попытаться найти такую декомпозицию функции, чтобы каждый
фрагмент полученного разложения зависел от возможно меньшего числа
аргументов, чем исходная функция. Попытаться выполнить это
различными способами.
Этап VIII. Выбрать из полученных на этапах V, VI, VII вариантов наиболее
подходящих с точки зрения поставленной задачи

Оценка качества функциональных схем
Основные критерии качества функциональной схемы:
1. Время задержки распространения сигнала – Т
2. Аппаратурные затраты – W

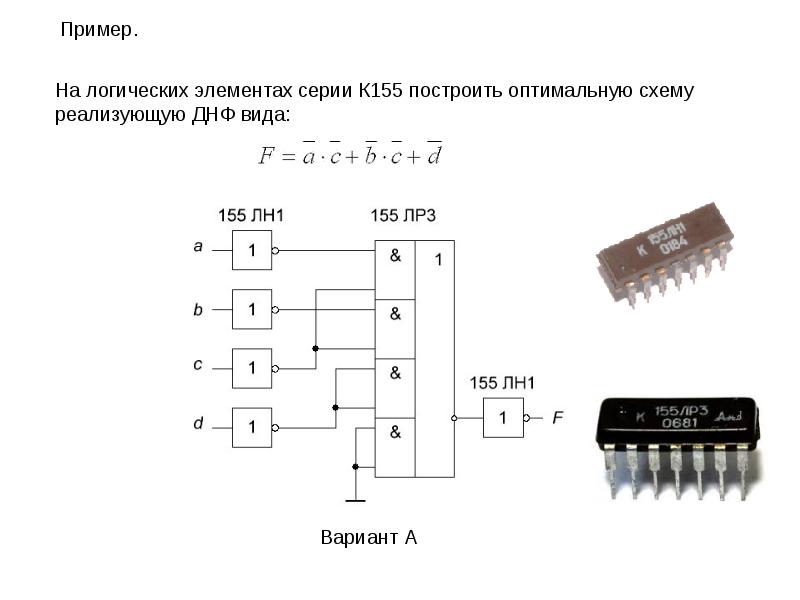
Пример.
На логических элементах серии К155 построить оптимальную схему
реализующую ДНФ вида:
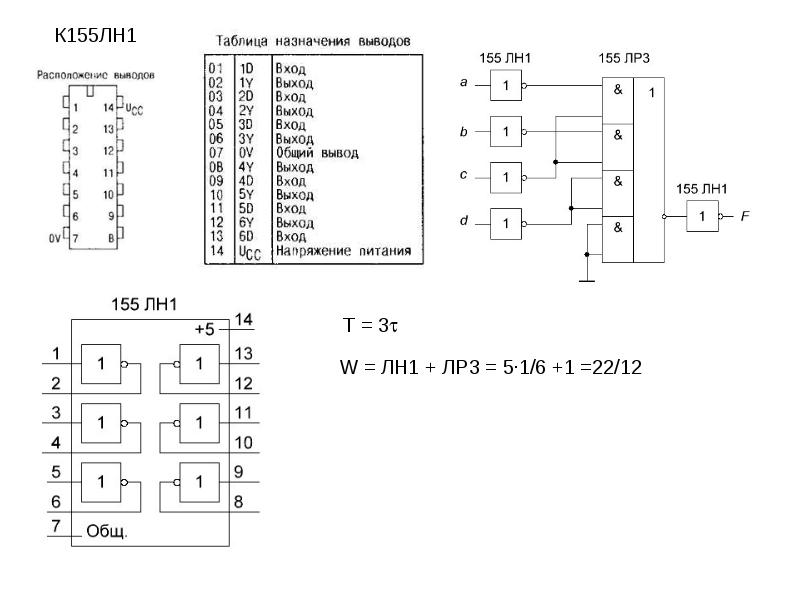
Вариант А

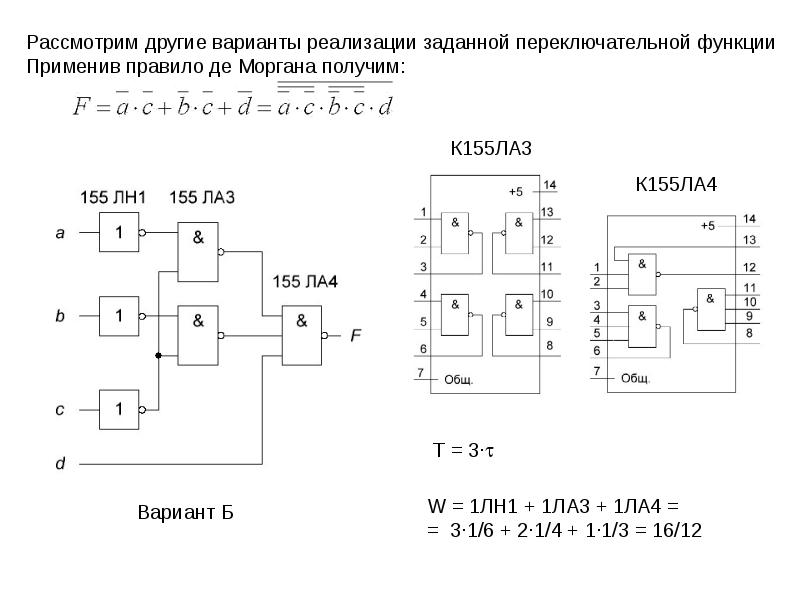
Рассмотрим другие варианты реализации заданной переключательной функции
Применив правило де Моргана получим:
К155ЛА3
К155ЛА4
Т = 3·t
Вариант Б
W = 1ЛН1 + 1ЛА3 + 1ЛА4 =
= 3·1/6 + 2·1/4 + 1·1/3 = 16/12

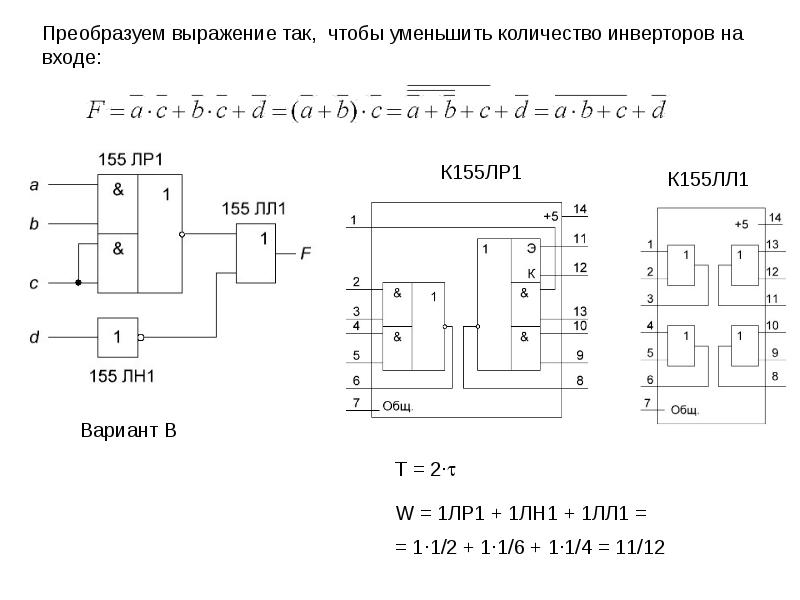
Преобразуем выражение так, чтобы уменьшить количество инверторов на
входе:
К155ЛР1
Вариант В
T = 2·t
W = 1ЛР1 + 1ЛН1 + 1ЛЛ1 =
= 1·1/2 + 1·1/6 + 1·1/4 = 11/12
К155ЛЛ1

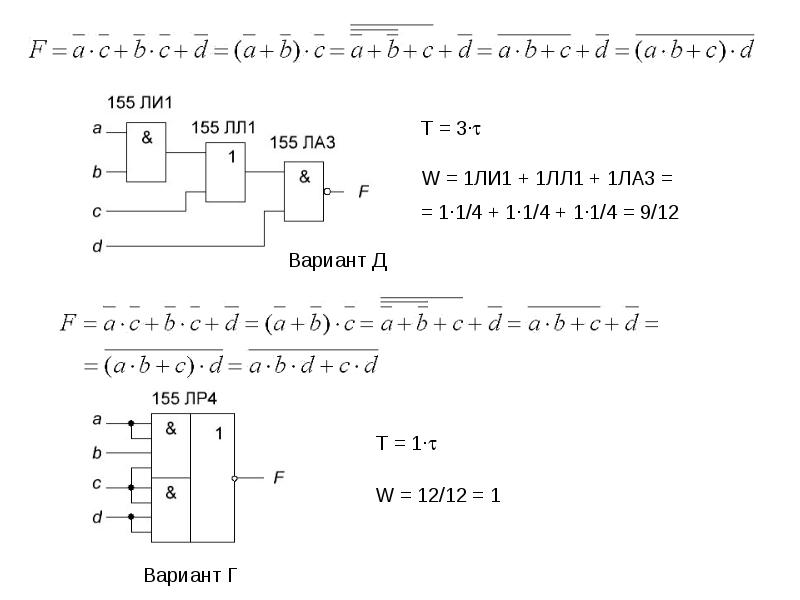
T = 3·t
W = 1ЛИ1 + 1ЛЛ1 + 1ЛА3 =
= 1·1/4 + 1·1/4 + 1·1/4 = 9/12
Вариант Д
T = 1·t
W = 12/12 = 1
Вариант Г

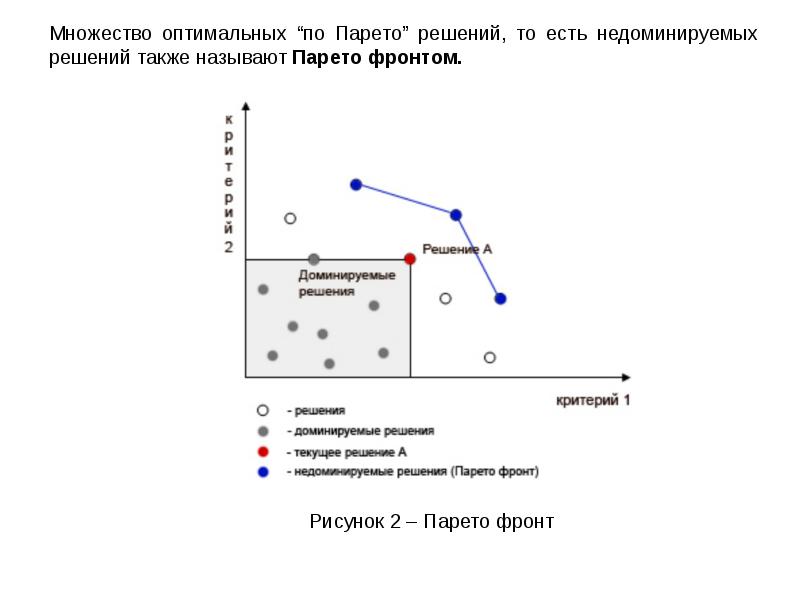
Множество оптимальных “по Парето” решений, то есть недоминируемых
решений также называют Парето фронтом.
Рисунок 2 – Парето фронт

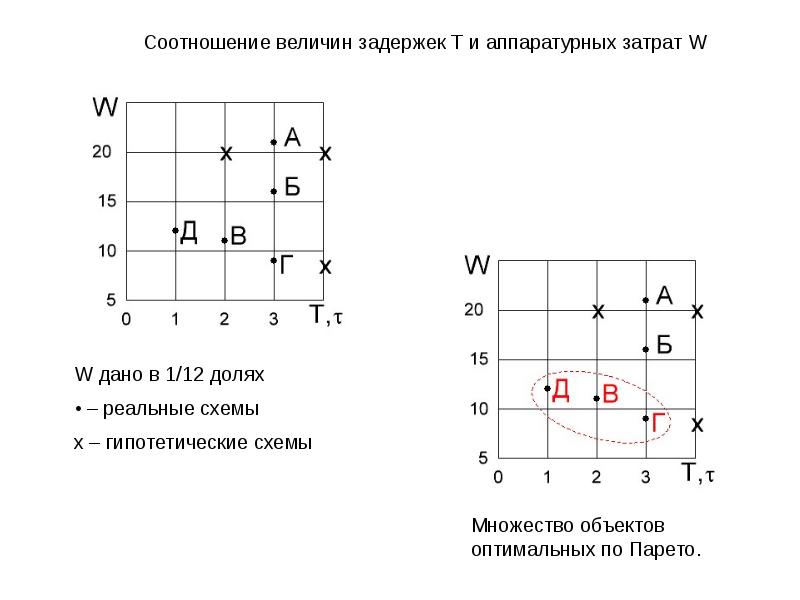
Соотношение величин задержек Т и аппаратурных затрат W
W дано в 1/12 долях
• – реальные схемы
х – гипотетические схемы
Множество объектов
оптимальных по Парето.

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

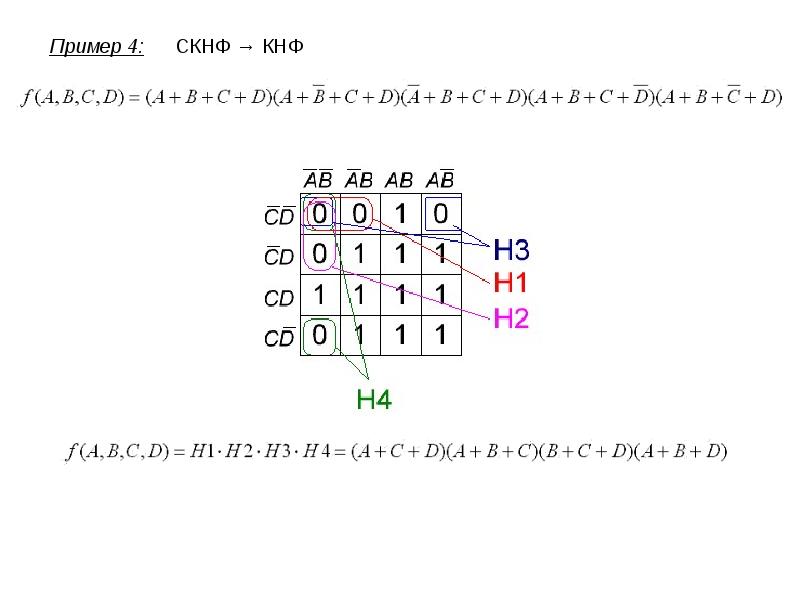
Задана переключательная функция:

1. составить СДНФ и СКНФ:

2. оптимизировать любую форму:

а) по карте Карно,

3. составить функциональные схемы:

3.1 для оптимизированной функции на любых логических элементах.

3.2 для не оптимизированной функции,

а) на логических элементах И-НЕ, И, НЕ;

б) на логических элементах ИЛИ-НЕ, ИЛИ, НЕ;

в) на любых логических элементах.

1. составим СДНФ и СКНФ:

Запишем функцию, представленную в виде таблицы истинности (таблица № 1), в виде совершенной дизъюнктивной нормальной формы:

Запишем СДНФ по составленным минтермам:

Составим макстермы для определения СКНФ:

Запишем СКНФ по составленным макстермам:

б) Составим СДНФ аналитически:

Здесь мы воспользовались тем, что - теорема поглощения, которая гласит, что умножение 1 на любую переменную даст нам ту же переменную. А также учли, что , т.е. если есть две одинаковые переменные, одну из них мы можем убрать.

Теперь для составления элементарных конъюнкций последовательно добавим недостающие переменные. Получим:

1. к переменной добавляем А и В:

2. к переменной добавляем С:

Запишем полученный СДНФ:

Затем аналитически найдем СКНФ.

К переменным и добавим последовательно другие переменные, получим:

Мы видим, что значения функций СДНФ и СКНФ, полученные табличным путем и аналитически совпадают, т.е. можно сделать вывод, что все преобразования сделаны, верно.

Читайте также: