Несобственные интегралы с бесконечными пределами интегрирования кратко
Обновлено: 05.07.2024
Пусть Y = F(X) – заданная и непрерывная для всех X ≥ α функция. Тогда для любого B ≥ A существует . Поставим вопрос о пределе этого интеграла при B → ¥.
Называется Несобственным интегралом От функции F(X) с бесконечным верхним пределом. Если этот предел существует и конечен, то несобственный интеграл называется Сходящимся. А если же он не существует или равен
± ¥, то этот несобственный интеграл называется Расходящимся.
Если F(X) ≥ 0 для всех X ≥ A, то У несобственного интеграла (6.1) имеется очевидный геометрический смысл, вытекающий из геометрического смысла (4.3) обычного определенного интеграла. Действительно, согласно рис. 5.14
Здесь S¥ - площадь бесконечно протяженной в направлении оси Ох криволинейной трапеции (рис. 5.15). Несмотря на свою бесконечную протяженность, она может оказаться и конечной. Но это может произойти, согласно рис. 5.15, лишь в случае, когда Y =F(X) → 0 при X →¥. Да и то, если функция Y =F(X) → 0 при X → ¥ достаточно быстро.
Пример 1. Найти площадь S¥, изображенную на рис. 5.16.
,
так как lnB → ¥ при B → ¥.
Итак, S¥ = ¥. И это несмотря на то, что функция при X → ¥. Несобственный интеграл , а значит, он расходится.
Пример 2. Найти площадь S¥ , изображенную на рис. 5.17.
Здесь S¥ = 1. То есть бесконечно протяженная площадь оказалась конечной. Это произошло потому, что подинтегральная функция при X → ¥ достаточно быстро (по крайней мере, гораздо быстрее, чем подинтегральная функция в предыдущем примере). Несобственный интеграл (число), а значит, он сходится.
Пример 3. Выяснить, сходится или расходится несобственный интеграл .
Решение. Вычислим это интеграл:
– не существует. Это очевидно, если вспомнить поведение графика функции Y= = SinX (синусоиды) при X → ¥. Таким образом, не существует, а значит, он расходится. Впрочем, это и не могло быть иначе, ибо подинтегральная функция cosX не стремится к нулю при Х → ¥.
Заметим, что при вычислении несобственных интегралов типа , как и при вычислении обычных определенных интегралов , можно сразу применять формулу Ньютона-Лейбница:
Если значение F(¥) существует и конечно, то согласно формуле (6.4) Ньютона-Лейбница сходится и несобственный интеграл .
Примечание. Совершенно аналогично интегралам с бесконечным верхним пределом можно рассматривать несобственные интегралы с бесконечным нижним пределом и даже с обоими бесконечными пределами интегрирования. То есть интегралы вида
Для их вычисления тоже можно применять формулу Ньютона-Лейбница.
Итак, (число), то есть этот интеграл сходится. Его величина π равна площади S¥ бесконечно протяженной в обе стороны фигуры, изображенной на рис. 5.18.
Заметим, что сам факт сходимости-расходимости несобственных интегралов с бесконечными пределами интегрирования не обязательно устанавливать с помощью прямого вычисления этих интегралов. Это вопрос часто можно решить и гораздо проще, сравнив данный несобственный интеграл с каким-либо другим, для которого сходимость-расходимость уже установлена.
Пусть, например, для всех имеет место неравенство F(X)£ G(X), Где Y = F(X) И Y = G(X) – Две непрерывные и неотрицательные функции (рис. 5.19). Тогда очевидно, что
Из неравенства (6.6) и рис. 5.19 очевидным образом следует так называемый Признак сравнения несобственных интегралов:
1) Если (число) - сходится, то и (число) - сходится, причем B
2) Если - расходится, то и - расходится.
3) Если - расходится, то - об этом интеграле ничего сказать нельзя.
4) Если (число) - сходится, то - об этом интеграле ничего сказать нельзя.
В качестве функции G(X), с которой на промежутке Сравнивают данную функцию F(X), часто используют функцию , а в качестве интеграла сравнения – интеграл , учитывая при этом, что при A > 0 и любых α функция - положительная и непрерывная функция, и что
Пример 5. Исследовать на сходимость-расходимость
Решение. Очевидно, что для всех X Î [2; ¥). Поэтому
Но согласно (6.8) интеграл сходится. Поэтому, по признаку сравнения, сходится и (он представляет собой некоторой конкретное число). Более того, предыдущее неравенство дает и оценку этого числа: так как, согласно (6.8), , то
Пример 6. Исследовать на сходимость-расходимость .
Решение. Очевидно, что
для всех X Î [3; ¥).
Но последний интеграл равен ¥. Следовательно, равен ¥ и . То есть он расходится.
Примечание. Справедлив и более сильный (обобщенный) признак сравнения, который применим для любых непрерывных и неотрицательных на
[A; ¥) функций. А именно, если
То есть если F(X) эквивалентна G(X) (F(X) ~ G(X)) при Х ® ¥, то несобственные интегралы
Сходятся или расходятся одновременно.
Пример 2. Исследовать на сходимость-расходимость .
Решение. Исследовав функцию , легко показать, что она определена, а следовательно и непрерывна для всех Х Î [10; ¥). При этом
Но, согласно (6.8), сходится. Поэтому и сходится.
Теперь перейдем к более сложному случаю несобственных интегралов с бесконечными пределами интегрирования, когда подинтегральная функция знакопеременна на своей области интегрирования (рис. 5.20). Тогда
Где А>0 – сумма площадей, находящихся над осью Ох, а В>0 – сумма площадей, находящихся под осью Ох.
Рассмотрим еще один несобственный интеграл, только уже от |F(X)|:
А) Допустим, что сходится. Тогда А + В – Конечное положительное число. А значит, и его положительные слагаемые А и В – Конечные положительные числа. Но тогда и их разность А – В – Конечное число (его знак может быть любым). А значит, согласно (6.10), несобственный интеграл сходится.
Б) Допустим, что расходится (равен +¥). Тогда сумма А +В = +¥, а значит, или А, или В, или оба они одновременно равны +¥. Но их разность А – В может оказаться как бесконечной, так и конечной. То есть может как сходиться, так и расходиться.
Если сходится, и при этом сходится, то говорят, что Сходится абсолютно. Величину абсолютно сходящегося несобственного интеграла можно и оценить:
Действительно, неравенство (6.12) равносильно очевидному неравенству
А если сходится, но при этом расходится, то говорят, что Сходится условно.
Пример 8. Показать, что сходится, причем абсолютно.
Решение. Рассматривая и используя признак сравнения (6.7), получаем:
Таким образом, сходится. Но тогда и сходится, причем абсолютно. Более того, мы можем произвести, используя неравенство (6.12), оценку этого интеграла:
То есть абсолютная величина интеграла заключена в пределах
[0; 1].
Пример 9. Доказать, что сходится, но условно.
Решение. Применим к этому интегралу формулу (5.5) интегрирования по частям:
Интеграл , как и рассмотренный в примере 8 интеграл , сходится. А значит, сходится и . Но сходится он условно, ибо (расходится).
Действительно, так как для всех Х, то для всех Х. А значит
Последний интеграл , как и аналогичные интегралы и , сходится (это можно подтвердить интегрированием по частям). То есть - число. А значит, (расходится). Но тогда и бóльший интеграл (расходится). То есть сходится, но условно.
Понятие несобственного интеграла и его геометрический смысл
Для вычисления несобственных интегралов требуются хорошие знания определенных интегралов. и пределов. По сути несобственный интеграл - особый случай определенного интеграла.
Как и при решении определенного интеграла, в результате решения несобственного интеграла должно получиться некоторое число. Но это лишь тогда, когда несобственный интеграл сходится. Если же он расходится, то ответ так и записывается: несобственный интеграл расходится.
А теперь - о том, почему несобственный интеграл - особый случай определенного интеграла.
Несобственные интегралы первого рода. По сути это тот же определённый интеграл, но в случаях, когда интегралы имеют бесконечный верхний или нижний пределы интегрирования, или оба предела интегрирования бесконечны.
Несобственные интегралы второго рода. По сути это тот же определённый интеграл, но в случаях, когда интеграл берётся от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не имеет, обращаясь в бесконечность.
Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f(x) непрерывна на отрезке [a, b], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.
Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f(x) находится выше оси Ox , определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f(x) , осью абсцисс и ординатами x = a , x = b . В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f(x) (на рисунке ниже - красного цвета), x = a и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:
Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.
Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае - расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.
Несобственные интегралы первого рода - с бесконечными пределами и их сходимость
Несобственные интегралы с бесконечным верхним пределом
Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.
Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f(x) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т.е.
Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся, а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.
Пример 1. Вычислить несобственный интеграл (если он сходится).
Решение. На основании определения несобственного интеграла находим
Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.
В следующем примере подынтегральная функция почти как в примере 1, только степень икса - не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?
Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).
Решение. Предположим сначала, что , тогда
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .
В первом случае, то есть при имеет место . Если , то и не существует.
Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .
Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:
Это обобщённая формула Ньютона-Лейбница.
Пример 3. Вычислить несобственный интеграл (если он сходится).
Решение. С помощью метода замены переменной можно получить очень полезную формулу:
Доказывать эту формулу нет необходимости, но запомнить стоит - пригодится. Итак, применяя эту формулу для нахождения первообразной получим
Итак, несобственный интеграл сходится и равен 1.
Пример 4. Вычислить несобственный интеграл (если он сходится).
Но предел не существует, т. е. данный несобственный интеграл расходится.
Пример 5. Вычислить несобственный интеграл (если он сходится).
Решение. Подынтегральная функция непрерывна в каждой точке, поэтому определённый интеграл от неё на отрезке [0, b] существует при всяком b . Находим этот интеграл:
Находим предел этого интеграла:
По определению, значение данного несобственного интеграла:
Несобственные интегралы с бесконечным нижним пределом
Аналогично определяется несобственный интеграл от непрерывной функции с бесконечным нижним пределом интегрирования , обозначаемый символом , а именно
Если этот предел существует (и, значит, конечен, то есть, равен некоторому числу, а не бесконечности), то данный несобственный интеграл называется сходящимся.
Пример 6. Вычислить несобственный интеграл с бесконечным нижним пределом(если он сходится).
Решение. Находим предел данного интеграла:
Вывод: данный несобственный интеграл сходится, а его значение равно -1/2.
Несобственные интегралы с двумя бесконечными пределами
Несобственный интеграл с двумя бесконечными пределами интегрирования , обозначаемый символом , нужно предварительно представить в виде суммы двух несобственных интегралов, один из которых с конечным верхним пределом интегрирования, другой - с конечным нижним пределом интегрирования, т.е.
причём этот несобственный интеграл считается сходящимся, если оба предела существуют, когда a и b независимо друг от друга неограниченно возрастают по абсолютной величине.
Пример 7. Вычислить несобственный интеграл с двумя бесконечными пределами (если он сходится).
Решение. На основании определения несобственного интеграла с двумя бесконечными пределами представляем данный интеграл как сумму двух несобственных интегралов:
Преобразуем подынтегральное выражение к форме , с помощью выделения полного квадрата:
По формуле находим:
(Эта формула, которой мы воспользовались, а также другие формулы, пригодные для интегрирования дробей, приведены в уроке Интегрирование некоторых рациональных дробей и иррациональностей).
Предел этого интеграла существует:
Второй интеграл, составляющий сумму, выражающую исходный интеграл:
Предел этого интеграла также существует:
Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:
Несобственные интегралы второго рода - от неограниченных функций и их сходимость
Пусть функция f(x) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b , в то время как во всех остальных точках отрезка она непрерывна.
Определение. Несобственным интегралом функции f(x) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.
Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае - расходящимся.
Используя формулу Ньютона-Лейбница, выводим:
Это также обобщённая формула Ньютона-Лейбница. Именно она применяется в решении задач на вычисление несобственных интегралов от неограниченных функций.
Пример 8. Вычислить несобственный интеграл (если он сходится).
Решение. Подынтегральная функция при неограниченно возрастает, а в точке x = 0 функция не определена, то есть, не существует. Применяем обобщённую формулу Ньютона-Лейбница:
(так как при x = 0 первообразная непрерывна). Вывод: данный несобственный интеграл сходится и равен -3/2.
Пример 9. Вычислить несобственный интеграл (если он сходится).
Решение. Подынтегральная функция непрерывна в каждой точке полуотрезка [0, 1] . В точке x = 1 функция обращается в бесконечность. Если взять , то на [0, c] подынтегральная функция непрерывна и, следовательно, существует интеграл.
Найдём предел этого интеграла:
Результат предыдущих действий: несобственный интеграл сходится и его значение мы нашли.
Пример 10. Исследовать на сходимость несобственный интеграл (верхний предел интегрирования больше нижнего).
Решение. Подынтегральная функция обращается в бесконечность при x = b , в остальных точках она непрерывна. Предположим сначала, что , тогда для :
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .
В первом случае, то есть при
Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .
К изучению несобственных интегралов лучше приступать в последнюю очередь в ходе изучения интегрального исчисления функции одной переменной. Читатель данного урока должен быть хорошо подкован в неопределенных интегралах, определенных интегралах, уметь находить площадь плоской фигуры с помощью определенного интеграла. Кроме того, потребуются знания простейших пределов и графиков элементарных функций. По логике изложения материала эта статья является продолжением урока Определенный интеграл. Как вычислить площадь фигуры.
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрирования
Иногда такой несобственный интеграл называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус :)
Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:
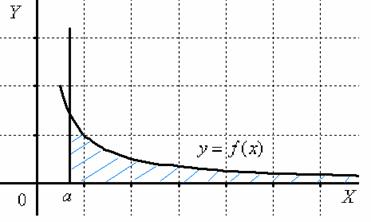
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади. При этом возможны следующие варианты:
2) Но. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится.
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.
Таким образом, несобственный интеграл может быть отрицательным.
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно. Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений, ибо лучше поздно, чем в армии.
Рассмотрим два классических примера:
Вычислить несобственный интеграл или установить его расходимость.
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно.
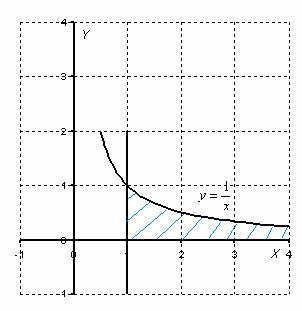
Применение нашей формулы и решение задачи выглядит так:
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций.
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
Подынтегральная функция непрерывна на
Несобственный интеграл расходится.
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет. Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Вычислить несобственный интеграл или установить его расходимость.
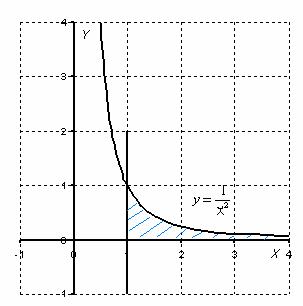
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
Подынтегральная функция непрерывна на
Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего), либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности, следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна на .
Интеграл не так прост, особенно для чайника. Что делать, если интеграл кажется не самым простым или не сразу понятно как его решать? В этом случае целесообразно применить алгоритм, о котором я уже рассказал в статье Определенный интеграл. Примеры решений.
Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Подынтегральная функция непрерывна на .
А сейчас два примера для самостоятельного решения.
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей.
Вычислить несобственный интеграл или установить его расходимость.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов. Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функций
Если подынтегральной функции не существует в точке
Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования. В этой связи проверим и верхний предел: . Здесь всё хорошо.
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
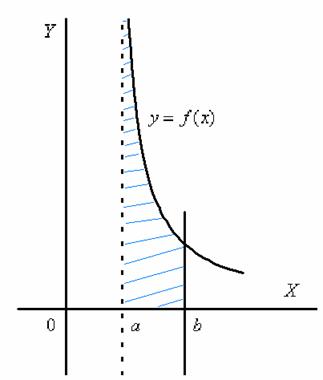
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа.
Посмотрим, как это реализуется на практике.
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле.
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .
А сейчас два примера для самостоятельного решения.
Вычислить несобственный интеграл или установить его расходимость.
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:
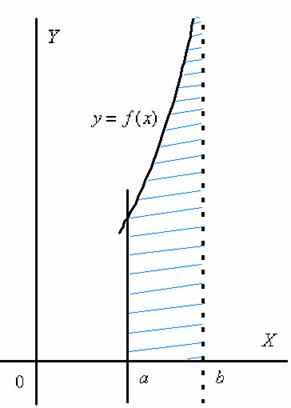
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению слева. По оси мы должны бесконечно близко приблизиться к точке разрыва слева.
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (устно проверяем, что с другим пределом интегрирования всё нормально!).
Для разнообразия я решу этот интеграл сразу – методом подведения функции под знак дифференциала. Те, кому трудно, могут сначала найти неопределенный интеграл по уже рассмотренной схеме.
Добавка обозначает, что предел у нас левосторонний, и к точке мы приближаемся по оси слева.
Разбираемся, почему дробь (это лучше делать устно или на черновике).
Подставляем под корень предельное значение :
и тогда
Несобственный интеграл расходится.
Будьте очень внимательны в знаках. Да, конечно, несобственный интеграл расходится, но и – это разные вещи, разные жанры, и если Вы недосмотрите за знаками, то, строго говоря, допустите серьезную ошибку.
И заключительные два примера для самостоятельного рассмотрения:
Вычислить несобственный интеграл или установить его расходимость.
Вычислить несобственный интеграл или установить его расходимость.
Решения и ответы:
Пример 4: Решение:
Подынтегральная функция непрерывна на .
Пример 5: Решение:
Подынтегральная функция непрерывна на .
Несобственный интеграл расходится.
Пример 7: Решение:
Подынтегральная функция терпит бесконечный разрыв в точке
Несобственный интеграл расходится.
Примечание: с пределом выражения можно разобраться следующим образом: вместо подставляем :
Пример 8: Решение:
Подынтегральная функция терпит бесконечный разрыв в точке
Примечание: Разбираемся в пределе выражения . Если , то (см. график логарифмической функции!), тогда: . Именно эти соображения и помечаются как
Пример 10: Решение:
Подынтегральная функция терпит бесконечный разрыв в точке
Пример 11: Решение:
Подынтегральная функция терпит бесконечный разрыв в точке
Несобственный интеграл расходится
Примечание: Разбираемся в пределе выражения . Если , то , и тогда . Будьте очень внимательны в знаках!
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Пример 32
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна всюду, и прямое решение таково:
Далее разделываемся с каждой половинкой по отдельности:
после чего суммируем трофеи:
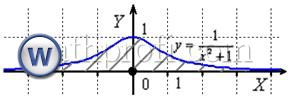
Теперь обратим внимание на подынтегральную функцию. Она является чётной и промежуток интегрирования симметричен относительно нуля. Знакомая геометрия:
В несобственных интегралах с бесконечными пределами интегрирования чётностью пользоваться МОЖНО. Аналогично определённому интегралу, промежуток интегрирования выгодно споловинить, а результат – удвоить:
Переходим к ещё более любопытному случаю:
Пример 33
Подынтегральная функция всюду непрерывна, нечётна и промежуток интегрирования симметричен относительно нуля. Но пользоваться этим НЕЛЬЗЯ, поскольку интеграл от такой функции может быть вовсе не определён. Как в нашем случае – по той причине:
– что этого предела не существует. Он не определён.
К такому же выводу можно прийти, если распилить пациента на две части:
и выполнить мартышкин труд:
Несмотря на то, что оба интеграла по отдельности расходятся – значение итогового интеграла не определено, ибо не определена сумма . К слову, для чётной функции получаются бесконечности одного знака, и всё хорошо.
Следует отметить, что в теории рассматривается особый случай – когда обе переменные стремятся к бесконечностям с одинаковой скоростью. Это выражается пределом:
и называется сходимостью по Коши. Само же значение предела называют главным значением несобственного интеграла и обозначают так: (Valeur principale de Cauchy).
Пример 34
Исследовать сходимость несобственного интеграла.
Полную и свежую версию данного курса в pdf-формате ,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
Читайте также:

