Момент импульса это кратко

Обновлено: 01.07.2024

Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

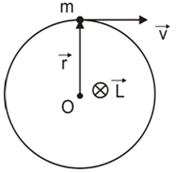
Моментом импульса L материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора r этой материальной точки, проведенного из точки О, на величину ее импульса Р(рис. 6):

где – радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, – импульс частицы.

Если твердое тело, вращающееся вокруг некоторой неподвижной оси z, представить в виде совокупности элементарных масс, и спроектировать моменты импульсов всех этих элементарных масс на это направление, получим момент импульса тела L_z относительно этой оси (L_z – скалярная величина).

Суммирование производим по всем элементарным массам m_i(имеющим линейную скорость v_i и радиус вращения r_i), на которые разбивается тело. Так как v_i=ωr_i, где ω - угловая скорость вращения тела, а I=∑m_ir_i 2 - момент инерции тела относительно данной оси, тогда момент импульса тела относительно оси z равен:

В случае тела, вращающегося вокруг оси симметрии, векторы L и ω имеют одинаковое направление и тогда:

= I .(1)

Продифференцируем выражение (1) по времени:

Таким образом, производная по времени от момента импульса твердого тела относительно оси вращения равна моменту сил относительно той же оси:

dL/ dt = M (3)

Из уравнения (3) видно, что если момент внешних сил, действующих на тело, равен нулю, то момент импульса тела остается постоянным.

Если M = 0, то: dL/dt = 0 ⇒ L = const. (4)

Выражение (4) представляет собой закон сохранения момента импульса:

момент импульса замкнутой системы тел не меняется со временем, причем это утверждение справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Этот закон выполняется только в инерциальных системах отсчета.

Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно поворота замкнутой системы в пространстве на любой угол.

В случае тела, вращающегося вокруг оси симметрии, векторы L и ω имеют одинаковое направление и тогда:

= I .(1)

Продифференцируем выражение (1) по времени:

dL/ dt = M (3)

Если M = 0, то: dL/dt = 0 ⇒ L = const. (4)

Выражение (4) представляет собой закон сохранения момента импульса:

Содержание

Момент импульса в классической механике

$<\displaystyle \scriptstyle <\mathbf Связь между импульсом >>$
и моментом >>" width="" height="" />

Определение

$<\displaystyle ~\mathbf <L> =\mathbf \times \mathbf ,>$

$<\displaystyle ~\mathbf <r> где >$
— радиус-вектор частицы относительно выбранного начала отсчёта, >" width="" height="" />
— импульс частицы.

$<\displaystyle \mathbf _=\sum \limits _\mathbf _>$
.

Вычисление момента

$<\displaystyle ~\mathbf <r> Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам >$
и >" width="" height="" />
. Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его

где >" width="" height="" />
— угол между >" width="" height="" />
и >" width="" height="" />
, определяемый так, чтобы к >" width="" height="" />
производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения. Направление поворота важно при вычислении, так как определяет знак искомой проекции.

=\mathbf \times \mathbf

=(\mathbf > +\mathbf > )\times \mathbf

=\mathbf > \times \mathbf

+\mathbf > \times \mathbf

=\mathbf > \times \mathbf

.>" width="" height="" />
=\mathbf \times \mathbf

=\mathbf \times (\mathbf > +\mathbf > )=\mathbf \times \mathbf > .>" width="" height="" />

Для систем, совершающих вращение вокруг одной из осей симметрии (вообще говоря, вокруг так называемых главных осей инерции), справедливо соотношение

$<\displaystyle ~\mathbf <L> =I>,>$

$<\displaystyle ~I> где$
— — вектор

Сохранение углового момента

Симметрия в физике
Закон сохранения
↕ …энергии
↔ Однородность	…импульса
○ Изотропия	…момента импульса
× Группа Лоренца	Относительность интервала (и др. момент силы:

$<\displaystyle \tau =<\frac <d\mathbf <L> >>= >>\times \mathbf +\mathbf \times >>=\mathbf \times \mathbf ,>$

$<\displaystyle \mathbf <L> _ <\mathrm <system>>=\mathrm \leftrightarrow \sum \tau _ <\mathrm <ext>>=0,>$

$<\displaystyle ~\tau _<ext> где >$
— момент одной из сил, приложенных к системе частиц.

Математически закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол " width="" height="" />
, радиус-вектор частицы с номером " width="" height="" />
изменятся на _=\delta \varphi \times \mathbf _>" width="" height="" />
, а скорости — _=\delta \varphi \times \mathbf _>" width="" height="" />
. Функция Лагранжа >>" width="" height="" />
системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому

$<\displaystyle \delta <\mathcal <L> >=<\mathcal <L>>(\mathbf _+\delta \mathbf _,\;\mathbf _+\delta \mathbf _)-<\mathcal <L>>(\mathbf _,\;\mathbf _)=\sum \limits _\left(>> <\partial \mathbf _>>\delta \varphi \times \mathbf _+>> <\partial \mathbf _>>\delta \varphi \times \mathbf _\right)=0.>$

С учетом >> <\partial \mathbf _>>=\mathbf

_,\;>> <\partial \mathbf _>>=\mathbf > _>" width="" height="" />
, где _>" width="" height="" />
— обобщенный импульс " width="" height="" />
-той частицы, каждое слагаемое в сумме из последнего выражения можно переписать в виде

$<\displaystyle <\dot <\mathbf >>_\,\delta \varphi \times \mathbf _+\mathbf _\,\delta \varphi \times \mathbf <\dot > _.>$

Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:

$<\displaystyle \delta <\mathcal <L> >=\delta \varphi \sum \limits _\left(\mathbf _\times >>_+ <\dot <\mathbf >>_\times \mathbf _\right)=\delta \varphi >\sum \limits _(\mathbf _\times \mathbf _)=\delta \varphi >>=0,>$

где, =\sum \mathbf _=\sum \mathbf _\times \mathbf

_>" width="" height="" />
— момент импульса системы. Ввиду произвольности " width="" height="" />
, из равенства >=0>" width="" height="" />
следует >>=0>" width="" height="" />
.

На орбитах момент импульса распределяется между собственным вращением планеты и момента импульса ее орбитального движения:

$<\displaystyle \mathbf _ <\mathrm <total>>=\mathbf _ <\mathrm <spin>>+\mathbf _ <\mathrm <orbit>>.>$

Момент импульса в электродинамике

$<\displaystyle ~\mathbf - >,>$

где " width="" height="" />
— электрический заряд, " width="" height="" />
— скорость света, " width="" height="" />
— векторный потенциал. Таким образом, гамильтониан (инвариантный) заряженной частицы массы " width="" height="" />
в электромагнитном поле:

$<\displaystyle H=<\frac <1> >\left(\mathbf - >\right)^+e\varphi ,>$

$<\displaystyle ~\varphi > где$
— скалярный потенциал. Из этого потенциала следует

Момент импульса в квантовой механике

Оператор момента

$<\displaystyle <\hat <\mathbf <L> >>=\mathbf \times <\hat <\mathbf >>,>$

$<\displaystyle \mathbf <r> где >$
и >>>" width="" height="" />
— координатный и импульсный оператор соответственно. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:

$<\displaystyle \mathbf <L> =-i\hbar (\mathbf \times \nabla ),>$

$<\displaystyle \nabla > где$
— оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства:

$<\displaystyle [L_ ,\;L_]=i\hbar \varepsilon _L_,\quad \left[L_,\;\mathbf ^\right]=0>$

и даже более важные подстановки с гамильтонианом частицы без заряда и спина:

$<\displaystyle \left[L_ ,\;H\right]=0>$

Симметрия вращения

Операторы момента импульса обычно встречаются при решении задач

Когда находят собственные значения этого оператора, получают следующее:

$<\displaystyle L^ \mid l,\;m\rangle =<\hbar >^l(l+1)\mid l,\;m\rangle >$
\mid l,\;m\rangle =\hbar m\mid l,\;m\rangle ,>" width="" height="" />

$<\displaystyle \langle \theta ,\;\varphi \mid l,\;m\rangle =Y_<l,\;m> (\theta ,\;\varphi )>$

— Вычисление момента импульса

Если имеется материальная точка массой " width="" height="" />
, двигающаяся со скоростью >" width="" height="" />
и находящаяся в точке, описываемой радиус-вектором >" width="" height="" />
, то момент импульса вычисляется по формуле:

$<\displaystyle ~\mathbf <L> =\mathbf \times m\mathbf ,>$

$<\displaystyle \times > где$
— знак векторного произведения.

Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки и векторно просуммировать их моменты как моменты импульса материальных точек, то есть взять

Литература

Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. Том 1. М.: Мир, 1984. 302с.
Блохинцев Д. И. Основы квантовой механики. 5-ое изд. Наука, 1976. — 664 с.
Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720c.
Варшалович Д. А., Москалев А. Н., Херсонский В. К.Квантовая теория углового момента. Л.: Наука, 1975.

Это незавершённая статья по физике. Вы можете помочь проекту, исправив и дополнив её.

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Момент импульса. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

Моме́нт и́мпульса (момент импульса относительно точки, также: кинетический момент, угловой момент, орбитальный момент, момент количества движения) — физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение [1] .

Для одной материальной точки момент импульса равен векторному произведению радиус-вектора точки на её импульс, для системы точек — сумме таких произведений. Стандартное обозначение: L > , единица измерения в СИ: м 2 кг/с. Величина L > зависит от выбора положения начала отсчёта радиус-векторов O.

Момент импульса замкнутой системы сохраняется. Он является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения. При наличии внешних сил производная момента импульса по времени равна моменту сил (относительно того же начала O).

Основное использование понятия момента импульса относится к задачам, связанным с реальным вращением (особенно при наличии центральной или осевой симметрии; тогда О обычно выбирается в центре или на оси). Но величина L > может быть вычислена и в других ситуациях, например для прямолинейного движения частицы мимо произвольной точки O, не лежащей на линии движения и условно принимаемой за центр.

В случае вращения твёрдого тела вокруг фиксированной оси часто используется не сам момент импульса, а его проекция L ∥ > на эту ось — такая величина называется моментом импульса относительно оси.

Понятие момента импульса было изначально введено в классической механике, но имеет обобщения в квантовой механике и электродинамике.

Момент импульса - векторная физическая величина характеризующая импульс, численно равная векторному произведению
Момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.

Момент импульса замкнутой системы сохраняется.
Эта величина называется моментом импульса относительно оси.

Закон сохранения момента импульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем. В упрощённом виде: , если система находится в равновесии.

Изотропность — одно из ключевых свойств пространства в классической механике. Пространство называется изотропным, если поворот системы отсчета на произвольный угол не приведет к изменению результатов измерений.

Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
Закон сохранения момента импульса является фундаментальным законом природы. Справедливость этого закона обусловливается свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета.

Справедливость закона сохранения момента импульса относительно неподвижной оси вращения можно продемонстрировать на опыте со скамьей Жуковского. Скамьей Жуковского называется горизонтальная площадка, свободно вращающаяся без трения вокруг неподвижной вертикальной оси. Человек, стоящий или сидящий на скамье, держит в вытянутых руках гимнастические гантели и приводится во вращение вместе со скамьей вокруг оси с угловой скоростью ω1. Приближая гантели к себе, человек уменьшает момент инерции системы, а так как момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость ее вращения ω2 возрастает.

Читайте также: