Мат логика кратко и понятно самое важное
Обновлено: 08.07.2024
В изучение оснований математики внесли свой вклад многие ученые, в том числе весьма выдающиеся – Г. Фреге Б. Рассел, Д. Гильберт, Л. Брауэр, Г. Вейль и др. Как всегда бывает в философии и смежных с ней областях, мнения ученых о природе кризиса и путях его преодоления были различны. В философии математики появились разные направления. Но следует сказать, что все они так или иначе способствовали развитию математической логики и углублению знаний математиков о природе понятий и методов своей науки. Был получен ряд результатов, по большей части неожиданных, которые, хотя и не привели к общему согласию в главных вопросах оснований математики (в том числе в вопросе о происхождении и значении парадоксов), но позволили гораздо лучше, чем раньше, представить себе, что можно и чего нельзя сделать с помощью формальных математических методов. Кроме того, сами логические исчисления дали возможность лучше понять, как устроены математические доказательства. Был подвергнут анализу и другой вид деятельности, составляющий не менее важную часть работы математика, чем доказательство теорем: вычисления и всевозможные формальные выкладки. В результате этого анализа возникла теория алгоритмов, также ставшая составной частью математической логики.
Современная математическая логика включает в себя также такие разделы, как многозначная логика(или нечеткая логика – fuzzy logic), в которой наряду с истинными и ложными суждениями имеются суждения, принимающие промежуточные между истиной и ложью значения. Модальная логика, оперирующая понятиями возможности и необходимости. Временная логика, в которой истинность суждений зависит от времени и др.
Говоря о современной математической логике, нельзя не сказать еще о том, что, начиная с конца 1930-х годов, идеи и методы математической логики используются и за пределами логики и математики.
Имеются две области такого их использования. Во-первых, это конструирование и эксплуатация различных автоматических устройств, в том числе вычислительных машин. В ряде случаев здесь используется технический аппарат математической логики; сверх того, что особенно важно, идеи математической логики – в первую очередь теории алгоритмов, но также и всей науки в целом – и свойственный ей стиль мышления оказали и продолжают оказывать очень большое влияние на те своеобразные области деятельности, содержанием которых является автоматическая переработка информации (информатика) и автоматизация процессов управления (кибернетика).
Следует сказать, что упомянутые области приложения идеи и методов математической логики имеют много точек соприкосновения: с одной стороны, формальные грамматики, созданные для исследования строения естественных языков, оказались также и удобным средством анализа языков программирования и других формальных языков; с другой – в информатике большое место занимают задачи, связанные с переработкой информации, выраженной на естественном языке, и требующие применения точных методов лингвистики.
Представляется вероятным, что со временем сфера внематематических приложений математической логики будет расширяться. Уже сейчас можно говорить, например, об использовании ее идей для некоторых разделов психологии.
Применение в логике математических методов становится возможным тогда, когда суждения формулируются на некотором точном языке. Такие точные языки имеют две стороны: синтаксис и семантику. Синтаксисом называется совокупность правил построения объектов языка (обычно называемых формулами). Семантикой называется совокупность соглашений, описывающих наше понимание формул (или некоторых из них) и позволяющих считать одни формулы верными, а другие — нет.
Важную роль в математической логике играют понятия дедуктивной теории и исчисления. Исчислением называется совокупность правил вывода, позволяющих считать некоторые формулы выводимыми. Правила вывода подразделяются на два класса. Одни из них непосредственно квалифицируют некоторые формулы как выводимые. Такие правила вывода принято называть аксиомами. Другие же позволяют считать выводимыми формулы , синтаксически связанные некоторым заранее определённым способом с конечными наборами выводимых формул. Широко применяемым правилом второго типа является правило modus ponens: если выводимы формулы и , то выводима и формула .
Отношение исчислений к семантике выражается понятиями семантической пригодности и семантической полноты исчисления. Исчисление И называется семантически пригодным для языка Я, если любая выводимая в И формула языка Я является верной. Аналогично, исчисление И называется семантически полным в языке Я, если любая верная формула языка Я выводима в И.
Математическая логика изучает логические связи и отношения, лежащие в основе логического (дедуктивного) вывода, с использованием языка математики [источник не указан 736 дней] .
Многие из рассматриваемых в математической логике языков обладают семантически полными и семантически пригодными исчислениями. В частности, известен результат К. Гёделя о том, что так называемое классическое исчисление предикатов является семантически полным и семантически пригодным для языка классической логики предикатов первого порядка. С другой стороны, имеется немало языков, для которых построение семантически полного и семантически пригодного исчисления невозможно. В этой области классическим результатом является теорема Гёделя о неполноте, утверждающая невозможность семантически полного и семантически пригодного исчисления для языка формальной арифметики.
Стоит отметить, что на практике множество элементарных логических операций является обязательной частью набора инструкций всех современных микропроцессоров и соответственно входит в языки программирования. Это является одним из важнейших практических приложений методов математической логики, изучаемых в современных учебниках информатики.
Математические методы дали логике такие преимущества, как высокая точность формулировок, возможность изучения более сложных, с точки зрения логической формы, объектов. Многие проблемы, исследуемые в математической логике, вообще невозможно было сформулировать с использованием только традиционных методов. Применение в логике математических методов становится возможным тогда, когда суждения формулируются на некотором точном (формализованном) языке. Такие точные языки имеют две составляющие: синтаксис (см. Синтактика) и семантику (см. Семантика). Синтаксисом называется совокупность правил построения объектов языка (обычно называемых формулами). Семантикой называется совокупность соглашений, описывающих наше понимание формул (или некоторых из них) и позволяющих считать одни формулы верными, а другие — нет.
Основным стимулом развития математической логики в начале XX века была проблема оснований математики. К. Вейерштрасс, Р. Дедекинд и Г. Кантор показали, что в качестве фундамента всей классической математики может рассматриваться арифметика целых чисел. Дедикинд и Пеано аксиоматизировали арифметику, а Фреге дал определение натурального числа как множества всех равномощных множеств. Таким образом, вся математика сводилась к теории множеств. Рефлексия над феноменом множеств привела к обнаружению ряда парадоксов в теории множеств, ответом на которые стало развитие четырёх направлений в основаниях математики:
- Логицизм (вся математика может быть дедуцирована из чистой логики без использования каких-либо специфических понятий, таких, как число или множество).
- Интуиционизм (нужна новая логика).
- Теоретико-множественный платонизм в виде аксиоматической теории множеств ZF (вводятся ограничения на образование множеств).
- Формализм (программа Гилберта).
Развитие и применение технического аппарата самой логики в первую очередь относится к программе Д. Гилберта (начиная с 1904 года), где была поставлена главная задача: найти строгое основание для математики посредством доказательства её непротиворечивости, то есть доказательства того факта, что в ней недоказуема никакая формула вида A вместе с формулой ~ А. Для этого потребовалось развить теорию доказательств, после чего, считал Гилберт, используя только финитные методы, можно будет доказать непротиворечивость теории множеств и самой теории действительных чисел и таким образом решить проблему оснований математики. Однако результат К. Гёделя о неполноте арифметики (1931) убедительно показал, что программа Гилберта невыполнима. Теорема Гёделя о неполноте утверждает, что всякая достаточно богатая теория необходимо содержит утверждения, которые нельзя ни доказать, ни опровергнуть, не опровергнув самой теории.
С годов XX века начинается современный этап развития математической логики. Он связан с применением точных методов при изучении формальных аксиоматических задач. Суть их состоит в описании рассматриваемой теории на базе строгого логико-математического языка (формализация), с последующими процедурами логического анализа теории, а именно с точки зрения непротиворечивости (например, таких теорий, как элементарная геометрия, арифметика, анализ достаточно надёжных оснований) и полноты. Основным объектом современной математической логики являются исчисления. В качестве их компонентов выступают: язык (формальный); аксиомы; правила вывода. На их основе стало возможным дать точное определение доказательства, получить точные утверждения о невозможности доказательства тех или иных предложений теории.
Обширным полем деятельности для современной математической логики является теория рекурсии, которая в первую очередь имеет дело с проблемой разрешимости: доказуема или нет формула A из некоторого множества посылок. Эти исследования привели к теориям вычислимости, к созданию компьютерных программ автоматического поиска доказательств. Решение проблемы разрешимости послужило основным стимулом для создания теории алгоритмов. Формулировка тезиса Чёрча — Тьюринга, утверждающего, что понятие общерекурсивной функции является уточнением интуитивного понятия алгоритма, стало наиболее важным достижением математической логики. Только после уточнения понятия алгоритма выяснилось, что в хорошо известных разделах математики существуют алгоритмически неразрешимые проблемы.
Важное место в современной математической логике занимает теория моделей (см. Теория моделей), которая изучает фундаментальные связи между синтаксическими свойствами множеств предложений формального языка, с одной стороны, и семантическими свойствами их моделей, с другой; и вообще, изучаются соотношения между моделями и теориями, а также преобразование моделей. Зачастую модели используются как инструмент для того, чтобы показать, что некоторая формула A не может быть дедуцирована из определённого множества постулатов или, если A есть аксиома, то показать недоказуемость A из остальных аксиом системы, к которой A принадлежит (если это возможно). Тогда A является независимой аксиомой.
Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.
Что такое алгебра и алгебра логики
Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.

Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.
Законы алгебры логики
Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.

Переместительный закон - предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.
Сочетательный закон - применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.
Распределительный закон - имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.
Закон двойственности и инверсии (закон Моргана) - основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.
Основные законы алгебры логики представлены в таблице:
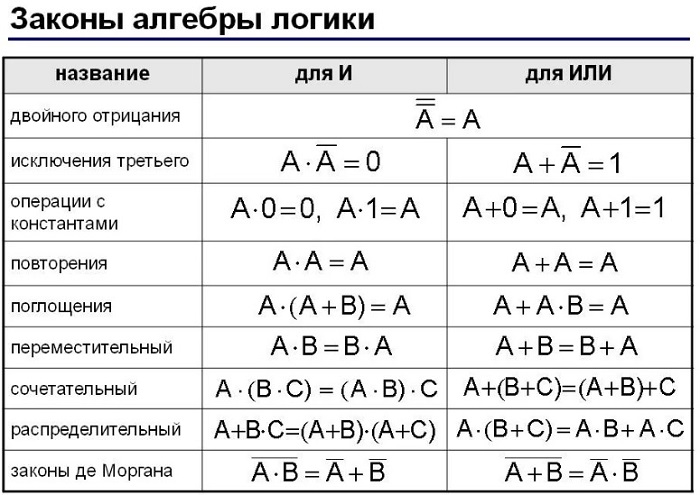
Логические выражения
В информатике предоставляется два вида высказываний: простое и сложное.

Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.
Нью-Йорк — столица США (ложное);
в России 1117 городов (верное).

Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.
Идёт дождь, а у меня нет зонта.
Основные логические операции
Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.
Логическое отрицание (инверсия) —НЕ
Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).
Таблица истинности инверсии:
Результаты операции НЕ следующие:
если исходное выражение истинно, то результат его отрицания будет ложным;
если исходное выражение ложно, то результат его отрицания будет истинным.
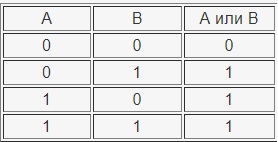
Логическое сложение (дизъюнкция, объединение) — ИЛИ
Таблица истинности операции ИЛИ:
Логическое умножение(конъюнкция) — И
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.
За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).
При всех остальных значениях операция будет ложной.
Таблица истинности операции И приведена ниже:
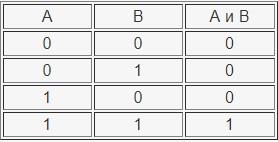
Логическое следование (импликация) — ЕСЛИ ТО
Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.
Таблица истинности операции ЕСЛИ ТО выглядит так:
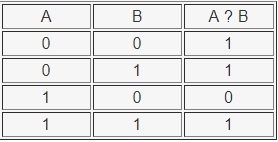
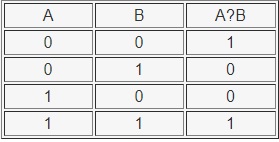
Операция эквивалентности (равнозначности) - А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.
И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.
Таблица истинности операции эквивалентности:
Читайте также:

