Конические сечения и их применение в технике кратко
Обновлено: 06.07.2024
Конические сечения – плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью.
За исключением вырожденных случаев, коническими сечениями являются эллипсы, гиперболы или параболы. С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек, удовлетворяющих уравнению второго порядка.
Открывателем конических сечений предположительно считается Менехм (IV в. до н. э.). Менехм использовал параболу и равнобочную гиперболу для решения задачи об удвоении куба.
В своих построениях Аполлоний использовал двуполостной круговой конус, поэтому впервые стало ясно, что гипербола – кривая с двумя ветвями. Со времен Аполлония конические сечения делятся на три типа в зависимости от наклона секущей плоскости к образующей конуса. Эллипс образуется, когда секущая плоскость пересекает все образующие конуса в точках одной его полости; парабола – когда секущая плоскость параллельна одной из касательных плоскостей конуса; гипербола – когда секущая плоскость пересекает обе полости конуса.
Изучая конические сечения как пересечения плоскостей и конусов, древнегреческие математики рассматривали их и как траектории точек на плоскости.
Эллипс можно определить как геометрическое место точек, сумма расстояний от которых до двух заданных точек постоянна; параболу – как геометрическое место точек, равноудаленных от заданной точки и заданной прямой; гиперболу – как геометрическое место точек, разность расстояний от которых до двух заданных точек постоянна.
Эти определения конических сечений как плоских кривых подсказывают и способ их построения с помощью натянутой нити.
Эллипс. Если концы нити заданной длины закреплены в точках (рис. 5.3.2), то кривая, описываемая острием карандаша, скользящим по туго натянутой нити, имеет форму эллипса. Точки и называются фокусами эллипса, а отрезки и между точками пересечения эллипса с осями координат – большой и малой осями . Если точки и совпадают, то эллипс превращается в окружность.
Гипербола. При построении гиперболы точка , острие карандаша, фиксируется на нити, которая свободно скользит по шпенькам, установленным в точках , как показано на рисунке 5.3.3, а. Расстояния подобраны так, что отрезок превосходит по длине отрезок на фиксированную величину, меньшую расстояния . При этом один конец нити проходит под шпеньком и оба конца нити проходят поверх шпенька . (Острие карандаша не должно скользить по нити, поэтому его нужно закрепить, сделав на нити маленькую петлю и продев в нее острие.) Одну ветвь гиперболы мы вычерчиваем, следя за тем, чтобы нить оставалась все время натянутой, и потягивая оба конца нити вниз за точку , а когда точка окажется ниже отрезка , придерживая нить за оба конца и осторожно отпуская ее. Вторую ветвь гиперболы мы вычерчиваем, предварительно поменяв шпеньки .
Ветви гиперболы приближаются к двум прямым, которые пересекаются между ветвями. Эти прямые, называемые асимптотами гиперболы , строятся как показано на рисунке 5.3.3, б. Угловые коэффициенты этих прямых равны где – отрезок биссектрисы угла между асимптотами, перпендикулярной отрезку ; отрезок называется сопряженной осью гиперболы, а отрезок – ее поперечной осью. Таким образом, асимптоты являются диагоналями прямоугольника со сторонами, проходящими через четыре точки параллельно осям. Чтобы построить этот прямоугольник, необходимо указать местоположение точек . Они находятся на одинаковом расстоянии, равном
от точки пересечения осей . Эта формула предполагает построение прямоугольного треугольника с катетами и и гипотенузой .
Если асимптоты гиперболы взаимно перпендикулярны, то гипербола называется равнобочной . Две гиперболы, имеющие общие асимптоты, но с переставленными поперечной и сопряженной осями, называются взаимно сопряженными .
Парабола. Фокусы эллипса и гиперболы были известны еще Аполлонию, но фокус параболы , по-видимому, впервые установил Папп (вторая пол. III в.), определивший эту кривую как геометрическое место точек, равноудаленных от заданной точки (фокуса) и заданной прямой, которая называется директрисой . Построение параболы с помощью натянутой нити, основанное на определении Паппа, было предложено Исидором Милетским (VI в.).
Расположим линейку так, чтобы ее край совпал с директрисой (рис. 5.3.4), и приложим к этому краю катет чертежного треугольника . Закрепим один конец нити длиной в вершине треугольника, а другой – в фокусе параболы . Натянув острием карандаша нить, прижмем острие в переменной точке к свободному катету чертежного треугольника. По мере того, как треугольник будет перемещаться вдоль линейки, точка будет описывать дугу параболы с фокусом и директрисой так как общая длина нити равна , отрезок нити прилегает к свободному катету треугольника, и поэтому оставшийся отрезок нити должен быть равен оставшейся части катета , то есть . Точка пересечения параболы с осью называется вершиной параболы , прямая, проходящая через , – осью параболы . Если через фокус провести прямую, перпендикулярную оси, то отрезок этой прямой, отсекаемый параболой, называется фокальным параметром . Для эллипса и гиперболы фокальный параметр определяется аналогично.
Заметим, что существуют и вырожденные случаи конических сечений. Они появляются в тех случаях, когда секущая плоскость проходит через вершину конуса. Если наклон плоскости к оси конуса больше, чем наклон образующей к оси, то сечением является точка – вершина конуса. Если эти углы совпадают, то есть секущая плоскость касается конуса, то коническим сечением будет одна прямая. Наконец, в случае, когда угол наклона секущей плоскости меньше, она пересекает конус по двум прямым.
В конические секции - кривые, полученные при пересечении плоскости конусом. Есть несколько способов сделать это; например, если плоскость проходит перпендикулярно осевой оси конуса, получается окружность.
Немного наклонив плоскость по отношению к осевой оси конуса, получается эллипс, замкнутая кривая, но если наклонить ее еще больше, получается парабола или гипербола, как видно на анимации на рисунке 1.
Конические сечения - это часть природы и окружающего нас мира. Инженерное дело, архитектура и астрономия - важные отрасли знаний, в которых используются конусы.
Условия для конических сечений
Конические сечения определяются как локусы, удовлетворяющие следующим условиям:
Притча
Это геометрическое место всех точек, лежащих на плоскости, равноудаленной от фиксированной точки, называемой фокус F и прямая также фиксированная, называемая директива.
Эллипс
Точка на плоскости принадлежит эллипсу, если сумма расстояний между этой точкой и двумя другими фиксированными точками, называемая прожекторы и расположен на большая ось эллипса, остается постоянным.
Длина окружности
Это геометрическое место всех точек, которые поддерживают одинаковое расстояние до другой точки, называемой центром. Это расстояние - это радио окружности.
Гипербола
Набор точек на плоскости такой, что разница между их расстоянием до двух фиксированных точек называется прожекторы, это постоянно.
Приложения
Давайте посмотрим на некоторые применения конических секций:
Притчи
-Когда объект брошен, траектория, которая следует за ним, имеет форму параболы.
-Параболы имеют заметное применение в машиностроении, например, в подвесных мостах кабели висят в форме парабол.
-Параболы также хороши для изготовления рефлекторов и телескопов. Это произошло благодаря интересному свойству: при размещении светильника в фокусе параболической поверхности поперечного сечения свет будет распространяться лучами, параллельными оси параболы.
-Если световые лучи, параллельные оси симметрии, приближаются к параболической поверхности, она концентрирует их в фокусе, что используется для создания рефлекторных телескопов, таких как телескоп Хейла на Монте-Паломаре.
Эллипсы
- Планеты солнечной системы движутся по эллиптическим траекториям, довольно близко к окружности в случае больших планет, включая Землю. Солнце не в центре, а в одном из фокусов.
-Эллипс широко используется в архитектуре как элемент декора и дизайна.
-При размещении рефлектора в одном из фокусов эллипса свет отражается в сторону другого фокусного расстояния. То же и со звуком. По этой причине в комнатах, имеющих форму эллипса, тех, кто говорит тихим голосом, находясь в одном фокусе, четко слышат слушатели, находящиеся в другом фокусе.
-Это же свойство имеет удивительное применение в области медицины. Камни в почках можно разрушить звуком. Ультразвуковые волны высокой интенсивности генерируются в одном из фокусов эллиптической ванны, наполненной водой, а пациент находится в другом фокусе. Звуковые волны ударяются и отражаются на камне, разбивая его на мелкие кусочки своей энергией, которую человек затем легко изгоняет во время мочеиспускания.
Гиперболы
-Некоторые кометы Солнечной системы следуют по гиперболическим траекториям, всегда с Солнцем в одном из фокусов.
- Очаги гипербол также очень интересны для изучения явлений отражения волн. Например, когда луч света направляется в фокус параболического зеркала, он отражается в другом фокусе, что является очень полезным свойством для создания телескопов, поскольку свет может быть сфокусирован на параболическом зеркале и перенаправлен в другое более подходящее место в зависимости от дизайн.
- Градирни АЭС имеют силуэт в виде гипербол.
-До появления GPS гиперболы использовались в навигации для определения местоположения лодок.Суда несли на борту приемники сигналов, излучаемых одновременно радиостанциями A и B, и компьютер отвечал за регистрацию разницы во времени прибытия сигналов, чтобы преобразовать их в разность расстояний. Таким образом, корабль находится на ответвлении гиперболы.
Процедура повторяется с двумя другими радиостанциями C и D, что помещает корабль в филиал еще одна гипербола. Конечное положение лодки - пересечение обеих гипербол.
Окружности
-Приход колеса изменил ход истории.
-Круговое движение очень распространено, многие части вращаются для создания различных эффектов, от мельниц до вентиляторов.
-Хотя траектории главных планет эллиптические, круговые траектории во многих случаях являются хорошим приближением.
-Окружность - частый элемент в архитектуре, дизайне, проектировании и строительстве. Список круглых или дискообразных деталей бесконечен: монеты, компакт-диски, часы и многое другое.
Примеры
Ниже показаны две коники на плоскости, окружность и эллипс.
У каждого есть аналитическое уравнение:
Длина окружности
(х-ч) 2 + (г-к) 2 = R 2
Где h и k - координаты центра, а R - радиус. Для окружности, показанной на рисунке, уравнение выглядит следующим образом:
(х + 2) 2 + (у-2) 2 = 4
Эллипс
Уравнение эллипса, центром которого является координатная точка (h, k):
[(х-ч) 2 / к 2 ] + [(y-k) 2 / b 2 ]= 1
Где a и b - полуоси эллипса. Для показанного эллипса центр находится в точке 0,0, большая полуось равна 5, а малая полуось равна 4. Следовательно, его уравнение:
Л.С. Понтрягин (1908 – 1988)
Призма переходит в генератрису, генератриса превращается в касательную, касательная съеживается в лемнискату, лемниската распадается на две окружности, одна из них вытягивается в эллипс, эллипс развертывается в параболу, парабола закручивается в спираль, спираль тихонько обвивает мозг, ее когда-то раскрутивший…
Мигель Отеро Сильва ((Miguel Otero Silva, 1908 – 1985),
Конические сечения – линии пересечения прямого кругового конуса с плоскостями, не проходящими через его вершину.
В зависимости от взаимного расположения конуса и секущей плоскости получают три типа конических сечений:
– секущая плоскость пересекает все образующие конуса в точках одной его плоскости (рис. 3.6.1 а); линия пересечения – замкнутая овальная кривая – эллипс; окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса;
– секущая плоскость параллельна одной из касательных плоскостей конуса (рис. 3.6.1. б); в сечении получается незамкнутая, уходящая в бесконечность кривая – парабола, целиком лежащая на одной полости;
– секущая пересекает обе полости конуса
(рис. 3.6.1. в) линия пересечения – гипербола – состоит из двух одинаковых незамкнутых, простирающихся в бесконечность частей (ветвей гиперболы), лежащих на обеих полостях конуса .
С точки зрения аналитической геометрии конические сечения – действительные, нераспадающиеся линии второго порядка.
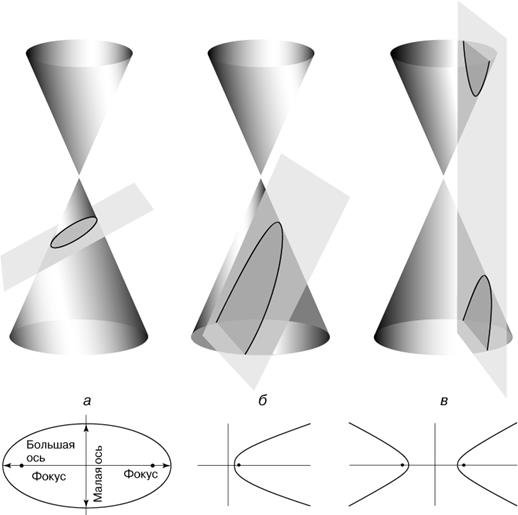
Рис. 3.6.1. Конические сечения как результат пересечения плоскости с конусом.
При определенном выборе системы координат (ось абсцисс – ось симметрии конического сечения, ось ординат – касательная к вершине конического сечения) уравнение конического сечения может быть приведено к виду
где и - постоянные, .
При уравнение определяет параболу: , при – эллипс, при – гиперболу.
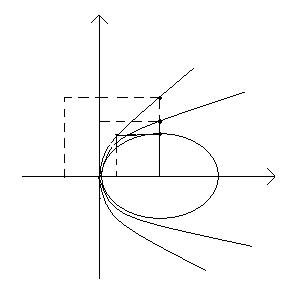 0 Рис.3.6.2. |
В переводе с др. греческого парабола означает – приложение, эллипс – недостаток (приложение с недостатком), гипербола – избыток (приложение с избытком). Эти названия возникли, потому что в греческой геометрии превращение прямоугольника, площадь которого равна , в прямоугольник такой же площади с основанием назывался приложением данного прямоугольника к этому основанию (рис. 3.6.2).
Создание Р. Декартом в ХVII веке координатного метода позволило от стереометрических определений конических сечений перейти к планиметрическим определениям этих кривых как множеств точек на плоскости.
Коническое сечение – множество точек, для каждой из которых отношение расстояний до данной точки (фокуса) к расстоянию до данной прямой (директрисы) равно данному положительному числу (эксцентриситету) . При коническое сечение – эллипс; при – гипербола; при – парабола.

Конические сечения часто встречаются в геометрических описаниях различных явлениях природы и человеческой деятельности. В науке конические сечения приобрели особое значение после того, как И. Кеплер (Kepler, Johann, 1609) открыл из наблюдений, а И. Ньютон (Isaac Newton, 1687) теоретически обосновал законы движения планет.
Пример 3.6.1. Составить уравнение линии, расстояние каждой точки которой от точки вдвое больше, чем от прямой Сделать чертеж.
Решение. Пусть – текущая точка линии. По условию задачи .
Возводя в квадрат и раскрывая скобки, получим
Получено каноническое уравнение гиперболы. Сделаем чертеж (рис. 3.6.3).
Пример 3.6.2. Составить уравнение линии, каждая точка которой равноудалена от точки и от прямой Сделать чертеж.
Решение. Если есть текущая точка линии, то по условию задачи , т.е.
Возведем в квадрат полученное уравнение, после преобразований запишем:
Получим уравнение параболы. Сделаем чертеж (рис. 3.6.4).
Л.С. Понтрягин (1908 – 1988)
Призма переходит в генератрису, генератриса превращается в касательную, касательная съеживается в лемнискату, лемниската распадается на две окружности, одна из них вытягивается в эллипс, эллипс развертывается в параболу, парабола закручивается в спираль, спираль тихонько обвивает мозг, ее когда-то раскрутивший…
Мигель Отеро Сильва ((Miguel Otero Silva, 1908 – 1985),
Конические сечения – линии пересечения прямого кругового конуса с плоскостями, не проходящими через его вершину.
В зависимости от взаимного расположения конуса и секущей плоскости получают три типа конических сечений:
– секущая плоскость пересекает все образующие конуса в точках одной его плоскости (рис. 3.6.1 а); линия пересечения – замкнутая овальная кривая – эллипс; окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса;
– секущая плоскость параллельна одной из касательных плоскостей конуса (рис. 3.6.1. б); в сечении получается незамкнутая, уходящая в бесконечность кривая – парабола, целиком лежащая на одной полости;
– секущая пересекает обе полости конуса
(рис. 3.6.1. в) линия пересечения – гипербола – состоит из двух одинаковых незамкнутых, простирающихся в бесконечность частей (ветвей гиперболы), лежащих на обеих полостях конуса .
С точки зрения аналитической геометрии конические сечения – действительные, нераспадающиеся линии второго порядка.

Рис. 3.6.1. Конические сечения как результат пересечения плоскости с конусом.
При определенном выборе системы координат (ось абсцисс – ось симметрии конического сечения, ось ординат – касательная к вершине конического сечения) уравнение конического сечения может быть приведено к виду
где и - постоянные, .
При уравнение определяет параболу: , при – эллипс, при – гиперболу.
 0 Рис.3.6.2. |
В переводе с др. греческого парабола означает – приложение, эллипс – недостаток (приложение с недостатком), гипербола – избыток (приложение с избытком). Эти названия возникли, потому что в греческой геометрии превращение прямоугольника, площадь которого равна , в прямоугольник такой же площади с основанием назывался приложением данного прямоугольника к этому основанию (рис. 3.6.2).
Создание Р. Декартом в ХVII веке координатного метода позволило от стереометрических определений конических сечений перейти к планиметрическим определениям этих кривых как множеств точек на плоскости.
Коническое сечение – множество точек, для каждой из которых отношение расстояний до данной точки (фокуса) к расстоянию до данной прямой (директрисы) равно данному положительному числу (эксцентриситету) . При коническое сечение – эллипс; при – гипербола; при – парабола.
Конические сечения часто встречаются в геометрических описаниях различных явлениях природы и человеческой деятельности. В науке конические сечения приобрели особое значение после того, как И. Кеплер (Kepler, Johann, 1609) открыл из наблюдений, а И. Ньютон (Isaac Newton, 1687) теоретически обосновал законы движения планет.
Пример 3.6.1. Составить уравнение линии, расстояние каждой точки которой от точки вдвое больше, чем от прямой Сделать чертеж.
Решение. Пусть – текущая точка линии. По условию задачи .
Возводя в квадрат и раскрывая скобки, получим
Получено каноническое уравнение гиперболы. Сделаем чертеж (рис. 3.6.3).
Пример 3.6.2. Составить уравнение линии, каждая точка которой равноудалена от точки и от прямой Сделать чертеж.
Решение. Если есть текущая точка линии, то по условию задачи , т.е.
Презентация на тему Конические сечения и их применения в технике, предмет презентации: Разное. Этот материал в формате pptx (PowerPoint) содержит 10 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Слайды и текст этой презентации

Конические сечения и их применения в технике

Цель:
изучение конических сечений и их применение в технике.
Задачи:
изучить виды конических сечений;
изучить применение их в технике.

- это плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через его вершину. Конические сечения впервые предложил использовать древнегреческий геометр Менехм, живший в IV веке до нашей эры, при решении задачи об удвоении куба. Коническими сечениями являются эллипсы, гиперболы или параболы.

Виды конических сечений
Конические сечения могут быть трёх типов:
1) Секущая плоскость пересекает все образующие конуса в точках одной его полости; линия пересечения есть замкнутая овальная кривая — эллипс; окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса.

2) Секущая плоскость параллельна одной из касательных плоскостей конуса; в сечении получается незамкнутая, уходящая в бесконечность кривая — парабола, целиком лежащая на одной полости.

3) Секущая плоскость пересекает обе полости конуса; линия пересечения — гипербола — состоит из двух одинаковых незамкнутых, простирающихся в бесконечность частей (ветвей гиперболы), лежащих на обеих полостях конуса.

Применение конических сечений в технике
Конические сечения часто встречаются в природе и технике. Например, орбиты планет, обращающихся вокруг Солнца, имеют форму эллипсов. В большинстве телескопов-рефлекторов, где применяются параболические зеркала, а также в антеннах радаров и специальных микрофонах с параболическими отражателями. В мощных прожекторах и автомобильных фарах используются параболические зеркала. Законе Бойля (связывающего давление и объем идеального газа) и законе Ома, задающего электрический ток как функцию сопротивления при постоянном напряжении.
Построение конических сечений
Изучая конические сечения как пересечения плоскостей и конусов, древнегреческие математики рассматривали их и как траектории точек на плоскости. Было установлено, что эллипс можно определить как геометрическое место точек, сумма расстояний от которых до двух заданных точек постоянна; параболу – как геометрическое место точек, равноудаленных от заданной точки и заданной прямой; гиперболу – как геометрическое место точек, разность расстояний от которых до двух заданных точек постоянна.
Эти определения конических сечений как плоских кривых подсказывают и способ их построения с помощью натянутой нити.
Читайте также:

