Кинематика вращательного движения кратко

Обновлено: 05.07.2024

В предыдущих лекциях мы познакомились с механикой материальной точ- ки. Использование модели материальной точки позволило нам сравнительно простыми средствами описать состояние материальной точки в любой момент времени и изменение этого состояния со временем (см. лекцию № 3, § 3 и вы- вод 7 из лекции № 3).

Модель абсолютно твердого тела (см. лекцию № 1, § 1) расширяет наши возможности и позволяет ввести различие между поступательным и враща- тельным движением.

Поступательным движениемназывается такое движение, при котором любая линия, проведенная в теле, остается параллельной самой себе.

Вращательным движениемназывается такое движение, при котором каждая точка твердого тела движется по своей окружности, центры всех окружностей лежат на одной прямой, называемой осью вращения.

На рис. 7.1а, 7.1б проиллюстрировано это различие. Отметим, что если на этих рисунках заменить изображенное затененным овалом твердое тело на ма- териальную точку, расположенную в центре масс тела, то различие между по- ступательным и вращательным движением исчезает. Более того, если ось вра- щения проходит через центр масс тела, то при использовании модели матери- альной точки говорить о вращении точки вокруг оси, проходящей через эту точку, не имеет никакого смысла.

Поступательное движение(рис. 7.1а). Любая линия, проведенная в твер- дом теле, при движении остается параллельной самой себе.

В данном примере траектория центра масс – окружность, остальные точки тела также движутся по окружностям, но центры этих ок- ружностей не лежат на одной прямой.

Вращательное движение(рис. 7.1б). Центр масс движется по окружности

того же радиуса. Каждая точка твердого тела движется по своей окружности; цен- тры всех окружностей лежат на прямой, называемой осью вращения.

Здесь, как и в предыдущем примере, центр масс тела движется по той же ок- ружности.

§ 2. Псевдовектор бесконечно малого поворота

Любое движение твердого тела можно разложить на поступательное и вращательное. Например, движение Земли состоит из поступательного движе- ния по эллиптической траектории вокруг Солнца и вращательного движения вокруг собственной оси. При изучении поступательного движения в большин-

стве случаев можно использовать модель матери- альной точки. При изучении вращательного дви- жения используют модель абсолютно твердого те- ла. При этом, в случае закрепленной оси вращения, положение абсолютно твердого тела в пространст- ве можно задать всего лишь одной переменной – зависящим от времени углом поворота (t). Ока- зывается, бесконечно малым углам поворота мож- но придать векторный характер, при этом направле- ние вектора связывают с направлением вращения.

Векторы, направления которых связываются с направлением вращения, называются псевдовекто- рами.

При повороте тела на угол вводят псевдо- вектор бесконечно малого поворота . В правой системе координат направление определяют правилом правого винта: винт, расположенный вдоль оси, вращается вместе с телом, направление

его поступательного движения определяет на-

правление псевдовектора (рис. 7.2).

В левой системе координат направление псевдовектора изменится на об- ратное, истинный вектор при этом не меняет направления.

Модуль псевдовектора равен величине угла поворота.

§ 3. Угловая скорость и угловое ускорение

Угловая скорость и угловое ускорение вводятся с помощью определений, аналогичных определениям скорости (2.1) и ускорения (2.7).

Угловая скорость

Угловой скоростью называется векторная величи- на, равная первой производной угла поворота тела по времени.

Псевдовектор направлен по оси вращения так же, как и псевдовектор (рис. 7.3).

Радиан – единица измерения угла – величина без-

размерная (см. на рис. 3.2), поэтому из (7.1) следу- ет, что угловая скорость измеряется в рад/с или в с -1 .

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени или второй производной угла пово- рота по времени.

Из (7.2) следует, что размерность углового ускорения

деления (7.2) следует, что угловое ускорение является псевдовектором.

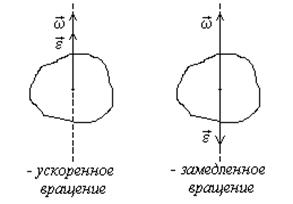
В случае закрепленной оси вращения направление углового ускорения совпадает с направлением угловой скорости при ускоренном движении и про- тивоположно при замедленном.

§ 4. Связь угловых и линейных кинематических величин

Абсолютно твердое тело можно рассматривать как систему материальных точек с неизменными расстояниями между ними. Эти точки при вращательном движении движутся по окружностям, центры которых лежат на оси вращения (см. рис. 7.1б). Линейные скорости v точек твердого тела и их линейные уско- рения a связаны с угловыми кинематическими величинами ω и ε , а также за-

висят от расстояния R материальной точки до оси вращения.

Найдем связь линейной скорости материальной точки твердого тела и угловой скорости. Из определе- ния радианной меры угла следует связь бесконечно малого отрезка пути ds материальной точки, удален- ной от оси вращения на расстояние R с углом поворо- та d (рис. 7.4, а также см. рис. 3.2). Используя эту связь и определение модуля линейной скорости (2.3), получим:

При поступательном движении тела все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения. Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.

Вращательное движение тела нельзя отождествить с движением какой-либо одной его точки. Различают следующие виды вращательного движения: вращение вокруг неподвижной оси, вращение вокруг свободных осей, вращение вокруг неподвижной точки – полюса (гироскопы, волчки), плоское движение (качение шара, цилиндра по горизонтальной поверхности).

Будем рассматривать только вращение тела вокруг неподвижной оси. В этом случае ось вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.

Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой – оси вращения.

Вращение твердого тела описывается углом поворота φ(t), на который повернулось тело за время t.

Угловая скорость w –векторная величина, характеризующая быстроту вращения тела, которая равна производной от угла поворота тела j по времени t:

.где dj – угол поворота тела за малое время dt.

Угловая скорость является псевдовектором. Вектор угловой скорости может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси, так, чтобы, смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки (рис. 1).

Равномерное вращательное движение

Если угловая скорость ω = const, то вращательное движение называется равномерным.

При равномерном вращении его быстроту также описывают частотой оборотов n и периодом вращения T.

Частота оборотов nравна числу оборотов, сделанных за единицувремени,

.где N– число оборотов за время t.

Т.к. за один оборот тело поворачивается на угол, равный 2p, то

j= 2p×N и w= 2p×n

Период вращения T– это время, за которое тело совершает один оборот.

[ω] = рад/с , [n] = об/с , [T] = с

Уравнение равномерного вращения имеет вид

В частном случае, когда начальный угол поворота

Угловую скорость равномерно вращающегося тела

можно выразить и так: ω = 2π /T,

.где: T – период вращения тела;

φ = 2π – угол поворота за один период.

Неравномерное вращение

Неравномерное вращение (угловая скорость изменяется со временем) характеризуется угловым ускорением e.

Угловое ускорение 1 - вектор, равный производной от угловой скорости w по времени t ,

.где dω – изменение угловой скорости за время dt.

Векторы и направлены по оси вращения тела. При ускоренном вращении тела направления векторов и совпадают, при замедленном – противоположны (рис. 2).

Равнопеременное вращение

Если угловое ускорение ε = const, то вращательное движение называется равнопеременным. Равнопеременное вращение характеризуется следующими уравнениями:

w ₀ и j ₀ – угловая скорость и угол поворота тела в начальный момент t₀ = 0,

Связь линейных и угловых характеристик

Если точка тела отстоит от оси вращения на расстоянии r, то за время dt она проходит путь

dS = dj×r

При вращении тела тангенциальное ускорение его точки

Нормальное ускорение точки тела

Полное ускорение, как указывалось ранее, определяют по формуле

Момент инерции

Момент инерции - скалярная величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.

Единица измерения СИ: кг·м². Обозначение: I или J.

Момент инерции тела относительно оси вращения зависит от массы тела и от распределения этой массы относительно этой оси. Чем больше масса тела и чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело.

Момент инерции элементарной (точечной) массы m_i, отстоящей от оси на расстоянии r_i, равен:

m_i — масса i-й точки,

r_i — расстояние от i-й точки до оси.

— масса малого элемента объёма тела ,

— расстояние от элемента до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Тело	Описание	Положение оси a	Момент инерции J_a
	Материальная точка массы m	На расстоянии r от точки, неподвижная
	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
Полый толстостенный цилиндр массы m с внешним радиусом r₂ и внутренним радиусом r₁	Ось цилиндра
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец
	Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы
Шар радиуса r и массы m	Ось проходит через центр шара

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния а между осями:

J = J_c + ma 2 .

где — полная масса тела (рис. 3).

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

Момент силы

Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают момент силы относительно центра (точки - полюса) и относительно оси.

Если имеется материальная точка О, к которой приложена сила , то момент силы относительно этой точки равен векторному произведению радиус-вектора , соединяющего точку О и точку приложения силы, на вектор силы :

Момент силы — аксиальный вектор[4]. Он направлен вдоль оси вращения.
Направление вектора момента силы определяется правилом буравчика, а величина его равна M (рис.4).

Модуль момента силы:

M =F•l =F•r•sin α,

где: M – момент силы (Ньютон•метр),

F – приложенная сила,

/r – расстояние от центра вращения до места приложения силы,

.l = r .sin α – плечо силы, т.е. длина перпендикуляра, опущенного из центра вращения на линию действия силы,

α — угол, между вектором силы F и вектором положения r.

Момент силы относительно оси величина алгебраическая, равная проекции на эту ось вектора Ммомента силы относительно любой точки О оси.

Пользуясь понятием момента силы можно по-новому сформулировать условия равновесия тела, закрепленного на оси. Это условие называется правилом моментов:

если на тело, закрепленное на оси, действует много сил, то для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю:

Считают момент силы положительным, если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис.5, силам F₁ и F₂ следует приписать положительный момент, а силе F₃— отрицательный.

Момент импульса

Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

Моментом импульса L материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора r этой материальной точки, проведенного из точки О, на величину ее импульса p (рис. 6):

где r – радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, p – импульс частицы.

Если твердое тело, вращающееся вокруг некоторой неподвижной оси z, представить в виде совокупности элементарных масс, и спроектировать моменты импульсов всех этих элементарных масс на это направление, получим момент импульса тела L_z относительно этой оси (L_z – скалярная величина).

Суммирование производим по всем элементарным массам m_i(имеющим линейную скорость v_i и радиус вращения r_i), на которые разбивается тело. Так как v_i=ωr_i, где ω - угловая скорость вращения тела, а I=∑m_ir_i 2 - момент инерции тела относительно данной оси, тогда момент импульса тела относительно оси z равен:

В случае тела, вращающегося вокруг оси симметрии, векторы L и ω имеют одинаковое направление и тогда:

= I .(1)

Продифференцируем выражение (1) по времени:

.dL_z / dt = I_z dω / dt = I_z e = M_z,

Таким образом, производная по времени от момента импульса твердого тела относительно оси вращения равна моменту сил относительно той же оси:

dL/ dt = M (3)

Из уравнения (3) видно, что если момент внешних сил, действующих на тело, равен нулю, то момент импульса тела остается постоянным.

Если M = 0, то: dL/dt = 0 ⇒ L = const. (4)

Выражение (4) представляет собой закон сохранения момента импульса:

момент импульса замкнутой системы тел не меняется со временем, причем это утверждение справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Этот закон выполняется только в инерциальных системах отсчета.

Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно поворота замкнутой системы в пространстве на любой угол.

Кинематика – это раздел механики, науки о механических движениях тел. Кинематика изучает движение тел, не рассматривая причины этих движений. Познакомимся с кинематикой вращательного движения.

Характеристики, описывающие вращение

Любое механическое движение может быть представлено суммой нескольких поступательных и вращательных движений. Основным отличием поступательного и вращательного движений является то, что при поступательном движении траектории всех точек тела представляют собой одинаковые фигуры, а при вращательном движении – это окружности различных радиусов, с центрами, расположенными на одной прямой.

Рис. 1. Примеры вращательного движения тел.

Поэтому кинематические характеристики вращательного движения, хотя и аналогичны кинематическим характеристикам поступательного движения, тем не менее, имеют заметные отличия.

Поскольку при поступательном движении все точки тела движутся одинаково – движение описывается только для одной точки, остальные движутся точно так же. Но что делать, если все точки движутся по-разному ?

Выход из ситуации лежит в нахождении общих параметров движения различных точек, и описание движения с помощью этих параметров. Несмотря на то, что при вращении точки твердого тела движутся по различным траекториям, эти траектории не только являются окружностями с центрами, лежащими на одной прямой, но и при движении по ним точки за равные промежутки времени описывают дуги одинакового угла. Таким образом, если связать движение с углом поворота, можно будет описывать вращения всех точек тела сразу.

То есть, для перехода от описания поступательного движения к вращательному, можно сделать замену характеристик:

перемещение $x(м)$ заменить на угол $\alpha (рад)$;
скорость $v(м/с)$ заменить на угловую скорость $\omega (рад/с)$;
ускорение $a(м/с^2)$ заменить на угловое ускорение $\varepsilon (рад/с^2)$.

Все расчеты вращательного движения производятся для угловых величин, и уже потом, зная угловые характеристики, при необходимости можно найти мгновенные линейные параметры.

Формулы кинематики для вращения

Получим кинематические формулы вращательного движения, произведя описанную замену. Формулы для поступательного движения:

Формулы после замены:

Кроме того, при решении задач полезно выразить время из одной формулы, и подставить его в другую, получив соотношение, нередко сильно упрощающее расчеты:

Следует отметить, что формулы для поступательного движения могут иметь векторную форму, все параметры могут быть направлены по-разному. При вращении движение совершается по фиксированной траектории. Поэтому значения в формулах для вращательного движения скалярны. В остальном – аналогия полная.

Рис. 2. Аналогия кинематических уравнений для поступательного и вращательного движения.

Связь угловых и линейных значений

При вращательном движении угол и пройденное расстояние прямо пропорциональны, коэффициент пропорциональности равен радиусу $R$. Поэтому для нахождения линейных значений достаточно умножить соответствующие угловые значения на радиус:

$S = \alpha R$
$v = \omega R$
$a = \varepsilon R$

Кроме линейного ускорения, меняющего модуль скорости, на любое вращательное тело также действует центростремительное ускорение, меняющее направление скорости. Оно равно:

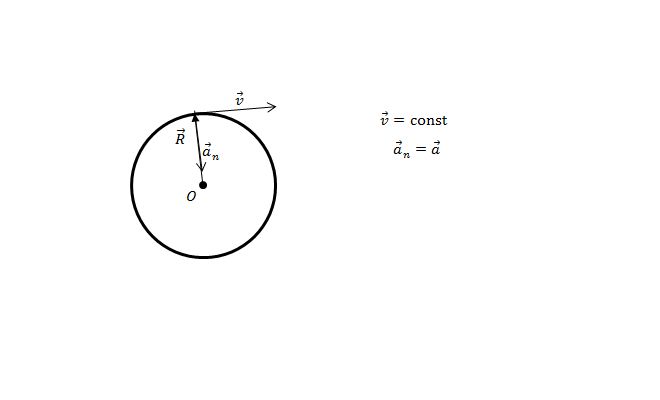
Рис. 3. Вектор центростремительного ускорения.

Что мы узнали?

При вращательном движении все точки тела проходят за одно и то же время одинаковый угол. Поэтому для описания вращательного движения используются угловые скорость и ускорение. Они прямо пропорциональны линейным, для их нахождения необходимо угловую величину умножить на радиус вращения.

Существует большое количество расчетных задач, которые моделируют явления, происходящие в различных вращающихся агрегатах или около них. При постановке подобной численной задачи важно выбрать способ описания вращения в численной модели, который будет корректен с точки зрения физики и оптимален с точки зрения производительности вычислений. FlowVision позволяет задавать вращение различными способами: с помощью вращающейся локальной системы координат; с помощью подвижных тел; с помощью скользящих поверхностей. С целью помочь пользователю разобраться с постановкой такого типа задач, рассмотрены примеры задач разного типа, начиная с физико-математических основ.

1. Кинематика вращательного движения

1.1. Вращательное движение материальной точки

Вращательное движение материальной точки (м.т.) вокруг неподвижной оси – это движение материальной точки по окружности радиуса R, центр которой лежит на неподвижной относительно данной системы отсчета прямой (ось вращения), перпендикулярной плоскости, в которой лежит траектория точки.

Рис.1.

Вращательное движение тела вокруг неподвижной оси - движение тела, при котором все его точки, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, называемой осью вращения. Тело, совершающее вращательное движение, имеет одну степень свободы, и его положение относительно данной системы отсчёта определяется углом поворота φ между неподвижной полуплоскостью и полуплоскостью, жёстко связанной с телом, проведёнными через ось вращения.

Рис.2.

1.2. Угол поворота

Угол φ считается положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az), и отрицательным, если по ходу часовой стрелки. Чтобы знать положение в любой момент времени, надо знать зависимость угла φ от времени t, т.е. φ=f(t).

Читайте также: