История возникновения комплексных чисел кратко

Обновлено: 05.07.2024

Комплексные числа были введены в математику для того, чтобы сделать возможной операцию извлечения квадратного корня из любого действительного числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату, уже не содержащему квадратный корень из отрицательного числа. В XVI веке итальянский математик Джероламо Кардано нашел формулу для решения кубического уравнения. Оказалось, когда кубическое уравнение имеет три действительных корня, в формуле Кардано встречается квадратный корень из отрицательного числа. Поэтому квадратные корни из отрицательных чисел стали употреблять в математике и назвали их мнимыми числами – тем самым они приобрели право на существование. Полные гражданские права мнимым числам дал немецкий математик Карл Фридрих Гаусс, который назвал их комплексными числами, дал геометрическую интерпретацию и доказал основную теорему алгебры, в которой говорится о том, что каждый многочлен имеет хотя бы один действительный корень.

ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА

Решение многих задач математики сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов в математике.

Так для решимости уравнений вида X+A=Bположительных чисел недостаточно. Например, уравнение X+5=2 не имеет положительных корней. Поэтому приходится вводить отрицательные числа и ноль.

На множестве рациональных чисел разрешимы алгебраические уравнения первой степени, т.е. уравнения вида A·X+B=0 (A 0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X 2 =2, X 3 =5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.

Но и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Простейшее из них – уравнение X 2 +1=0. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.

Выясним предварительно, какой вид должны иметь комплексные числа. Будем считать, что на множестве комплексных чисел уравнение X 2 +1=0 имеет корень. Обозначим этот корень буквой i. Таким образом, i – это комплексное число, такое, что i 2 = –1.

Как и для действительных чисел, нужно ввести операции сложения и умножения комплексных чисел так, чтобы сумма и произведение их были бы комплексными числами. Тогда, в частности, для любых действительных чисел A и B выражение A+B·i можно считать записью комплексного числа в общем виде. Название “комплексное” происходит от слова “составное”: по виду выражения A+B·i.

Комплексными числами называют выражения вида A+B·i, где A и B –действительные числа, а i – некоторый символ, такой что i 2 = –1, и обозначают буквой Z.

Число A называется действительной частью комплексного числа A+B·i, а число B – его мнимой частью. Число i называется мнимой единицей.

Например, действительная часть комплексного числа 2+3·i равна 2, а мнимая равна 3.

Для строгого определения комплексного числа нужно ввести для этих чисел понятие равенства.

Два комплексных числа A+B·i и C+D·i называются равными тогда и только тогда, когда A=C и B=D, т.е. когда равны их действительные и мнимые части.

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОМПЛЕКСНОГО ЧИСЛА

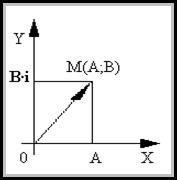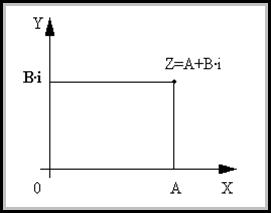
Действительные числа геометрически изображаются точками числовой прямой. Комплексное число A+B·i можно рассматривать как пару действительных чисел(A;B). Поэтому естественно комплексное число изображать точками плоскости. В прямоугольной системе координат комплексное число Z=A+B·i изображается точкой плоскости с координатами (A;B), и эта точка обозначается той же буквой Z. Очевидно, что получаемое при этом соответствие является взаимно однозначным. Оно дает возможность интерпретировать комплексные числа как точки плоскости, на которой выбрана система координат. Такая координатная плоскость называется комплексной плоскостью. Ось абсцисс называется действительной осью, т.к. на ней расположены точки соответствующие действительным числам. Ось ординат называется мнимой осью – на ней лежат точки, соответствующие мнимым комплексным числам.

Не менее важной и удобной является интерпретация комплексного числа A+B·i как вектора, т.е. вектора с началом в точке

O(0;0) и с концом в точке М(A;B).

Соответствие установленное между множеством комплексных чисел, с одной стороны, и множествами точек или векторов плоскости, с другой, позволяет комплексные числа точками или векторами.

МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА

Пусть дано комплексное число Z=A+B·i. Сопряженным с Z называется комплексное число A – B·i, которое обозначается , т.е.

= =A – B·i.

Отметим, что = A+B·i, поэтому для любого комплексного числа Z имеет место равенство =Z.

Модулем комплексного числа Z=A+B·i называется число и обозначается , т.е.

= = (1)

Из формулы (1) следует, что для любого комплексного числа Z, причем =0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Для любого комплексного числа Z справедливы формулы:

СЛОЖЕНИЕ И УМНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ

Суммойдвух комплексных чисел A+B·i и C+D·i называется комплексное число (A+C) + (B+D)·i, т.е. (A+B·i) + (C+D·i)=(A+C) + (B+D)·i

Произведением двух комплексных чисел A+B·i и C+D·i называется комплексное число (A·C – B·D)+(A·D+B·C) ·i, т.е.

(A + B·i)·(C + D·i)=(A·C – B·D) + (A·D + B·C)·i

Из формул вытекает, что сложение и умножение можно выполнять по правилам действий с многочленами, считая i 2 = –1. Операции сложения и умножения комплексных чисел обладают свойствами действительных чисел. Основные свойства:

Комплексные числа являются расширением множества действительных чисел.

Основные определения

Комплексным числом называется выражение вида $z=a+b_i$

Действительное число $a$ называется действительной частью комплексного числа $z=a+b_i$ и обозначается $b=\operatorname z$ .

Действительное число $b$ называется мнимой частью числа $z=a+b_i$ и обозначается $b=\operatorname z$ .

Историческая справка

Исторически комплексные числа впервые были введены в связи с выведением формулы вычисления корней кубического уравнения $x^3=px + q$ Итальянский математик Никколо Фонтана Тартальей (1499 - 1557) в первой половине 16 века получил выражение для корня такого уравнения через некоторые параметры, для нахождения которых составляется система. Но было выяснено, что такая система не для всех кубических уравнений имела решение в действительных числах. Это непонятное на то время явление объяснил в 1572 году Рафаэль Бомбелли (1526 - 1572), что по сути было введением комплексных чисел и действий над ними. Но долгое время полученные результаты многими учеными считались сомнительными и лишь в 19 веке после появления трудов немецкого математика, механика, физика, астронома и геодезиста Карла Фридриха Гаусса (1777 - 1855) существование комплексных чисел стало общепризнанным.

Хотя согласно некоторым источникам, по-видимому, мнимые величины были впервые упомянуты в 1545 году в известном труде "Великое искусство, или об алгебраических правилах" итальянского математика, инженера, философа, медика и астролога Джероламо Кардано (1501 - 1576), в рамках формального решения задачи по вычислению двух чисел, которые в сумме дают 10, а при перемножении дают 40.

Выражения, представимые в виде $a+b \sqrt$, появляющиеся при решении квадратных и кубических уравнений, стали называть "мнимыми" в 16-17 вв. с подачи французского философа, математика, механика, физика и физиолога Рене Декарта (1596-1650), который называл их так, отвергая их реальность.

Одним из способов построения множества комплексных чисел состоит в том, что множество действительных чисел расширяют присоединением к этому множеству корня уравнения $x^2+1=0$.

Продолжительное время стоял вопрос, является ли множество комплексных чисел замкнутым, то есть все ли операции над комплексными числами являются приводят к комплексным или вещественным результатам, или, например, извлечение корня может привести к открытию ещё какого-то нового типа чисел. Задача о выражении корней $n$-ой степени из рассматриваемого комплексного числа была решена в работах английского математика Абрахама де Муавра (1667 - 1754) в 1707 году и английского математика и философа Роджера Котса (1682 - 1716) в 1722 году.

Символ $i$ для обозначения мнимой единицы предложил швейцарский, немецкий и российский математик и механик Леонардо Эйлер в 1777, взявший для этого первую букву латинского слова "imaginarius" - мнимый. Он же распространил все стандартные функции, включая логарифм, на комплексную область.

Сегодня поговорим о возникновении комплексных чисел - наверное самых важных "виртуальных" конструктах, которые придумали математики, а используют почти все без исключения. Поехали!

История комплексных чисел, как считается, начинается в 16 веке, когда итальянский математик Джелорамо Кардано при решении кубических уравнений получил весьма интересные значения с отрицательным подкоренным выражением.

Прим. автора. Формула Кардано, которую я впервые увидел в классе 6-ом в энциклопедии "Аванта+" произвела неизгладимое впечатление своей красотой и, в то же время, недоступностью.

Однако первым, кто стал применять комплексные числа при решении кубических уравнений был Рафаэль Бомбелли . Попробуем пройти его путь. Бомбелли решал следующее кубическое уравнение:

Для решения он использовал те самые формулы Кардано:

Обратите внимание, p = -15, q = -4. Уравнение, решаемое Бомбелли называется приведенным кубическим уравнением.

Попробуем посчитать по этим формулам:

Вот тут и появляется то самое отрицательное подкоренное выражение . Бомбелли еще не вводил обозначение i^2 = -1 (его придумал Леонард Эйлер), но мы сделаем это для простоты понимания.

Итак, что делать с этим выражением? Бомбелли путем подбора определил, что выражение под знаком кубического корня можно представить как куб суммы . Вот, посмотрите:

Установление возникновения необходимости извлекать квадратные корни из отрицательных чисел. Особенности использования аппарата комплексных чисел. Основные понятия и арифметические действия над ними. Определение основных свойств операции сопряжения.

Рубрика	Математика
Вид	реферат
Язык	русский
Дата добавления	03.11.2015
Размер файла	23,4 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

История возникновения комплексных чисел

В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел.

Читайте также: