Интегральная формула лапласа кратко

Обновлено: 08.07.2024

Решение. Используем формулу полной вероятности. Относительно наудачу взятого зерна есть гипотезы: В₁ – зерно I сорта, Р(В₁) = 0,96; В₂ – зерно II сорта, Р(В₂) = 0,01; В₃ – зерно III сорта, Р(В₃) = 0,02; В₄ – зерно IV сорта, Р(В₄) = 0,01.

Пусть событие А: колос содержит не менее 50 зерен.

Пример 6. Вероятность того, что расход воды на некотором предприятии окажется нормальным (не более определенного количества литров в сутки) равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход воды будет нормальным любые трое суток.

Решение. Используем формулу Бернулли , где , .

Пример 7. Вероятность всхожести семян данного растения постоянна и равна р = 0,9. Было посажено 2500 семян. Какова вероятность того, что прорастут: а) ровно 2250 семян; б) не более 2200 семян.

Решение. а) Используем локальную теорему Лапласа (приложение А):

, где n=2500, m=2250, p=0,9, q=0,1

б) Используем интегральную теорему Лапласа (приложение Б):

Пример 8. Вероятность выпуска бракованного изделия р = 0,015. Найти вероятность того, что среди 400 проверенных изделий бракованных будет ровно пять.

Решение. Условия задачи позволяет использовать формулу Пуассона при

λ = np = 400∙0,015 = 6. Следовательно:

Вопросы для самоконтроля.

1. Что называется элементарным событием или элементарным исходом?

2. Что такое пространство элементарных событий?

3. Какое событие называется достоверным, невозможным?

4. Может ли сумма двух событий совпадать с их произведением?

5. Какие события называются несовместными?

6. Какие события называются совместными?

7. Какое событие называется противоположным для данного события?

8. Какие значения может принимать вероятность события?

9. В каком случае вероятность события вычисляется по формуле классической вероятности?

10. Что такое перестановки? Что такое сочетания? Что такое размещения?

11. Как определяется условная вероятность события?

12. Как пересчитать вероятности гипотез после опыта с учётом наблюдаемого результата?

13. В чем заключается определение повторных независимых испытаний?

14. Как найти наиболее вероятное число появлений события в данной серии опытов?

15. При решении каких задач применяется формула Бернулли?

16. Является ли формула Бернулли точной или приближенной?

17. В чем заключается локальная и интегральная теоремы Лапласа?

18. Какие свойства имеют функции j(x) и Ф(x)?

2 Случайные величины. Задачи типа 2, 3

Случайной величиной называют такую величину, которая в результате испытания может принять только одно числовое значение из своих возможных значений, заранее неизвестно какое именно, и обусловленное случайными причинами.

Различают дискретные и непрерывные случайные величины. Обозначают случайные величины прописными буквами: X, Y, Z,…, а их возможные значения строчными буквами, например, .

Случайная величина называется дискретной,если она принимает отдельные изолированные значения, которые можно пересчитать, с соответствующими вероятностями. Число значений дискретной случайной величины может быть конечным или бесконечным. Например, дискретная случайная величина Х – число попаданий при трех выстрелах, имеет четыре возможных значения: 0, 1, 2, 3.

Случайная величина называется непрерывной,если ее возможные значения заполняют некоторый интервал полностью. Например, рост человека, вес человека и т.п.

Законом распределения случайной величины называется любое соотношение между возможными значениями случайной величины и соответствующими вероятностями. Эту зависимость можно задать таблично, аналитически или графически.

Если случайная величина Х – дискретная с конечным множеством возможных значений, то ее закон распределения обычно задают в виде таблицы, в первой строке которой указывают все возможные значения случайной величины, расположенные по возрастанию, во второй строке – вероятности, с которыми она их принимает:

x_i	x₁	x₂	. . .	x_n
p_i	p₁	p₂	. . .	p_n

В этом случае группа событий - есть полная группа событий и .

Закон распределения дискретной случайной величины можно задать графически в виде многоугольника распределения, если на плоскости построить точки с координатами (x_i, p_i) и соединить их ломаной линией.

Закон распределения непрерывной случайной величины задается интегральной или дифференциальной функциями распределения.

Интегральной функцией распределения F(x) называется функция одного переменного x, определенная на всей числовой оси и для каждого x значение функции F(x) = P(X 2 ∙D(X);

Для дискретной случайной величины Х расчетная формула дисперсии:

для непрерывной величины:

Среднее квадратическое отклонениеслучайной величины Х равно корню квадратному из D(X): .

Пример 1. На пути движения автомобиля 4 светофора, каждый из которых с вероятностью р = 0,5 разрешает или запрещает движение автомобиля. Составить закон распределения величины Х – количества светофоров, которые автомобиль минует без остановки. Найти числовые характеристики М, D, величины Х, построить график F(x) и многоугольник распределения.

Решение. Возможные значения величины Х: 0, 1, 2, 3, 4. Вероятности этих значений найдем по формуле Бернулли при n = 4, p = 0,5 и q = 0,5.

Таким образом, закон распределения величины Х:

х_i	0	1	2	3	4
р_i	0,0625	0,25	0,375	0,25	0,0625

Найдем числовые характеристики дискретной случайной величины Х.

Построим многоугольник распределения:

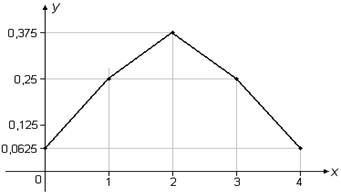
Рисунок 2.1 – Многоугольник распределения

Построим функцию распределения F(x):

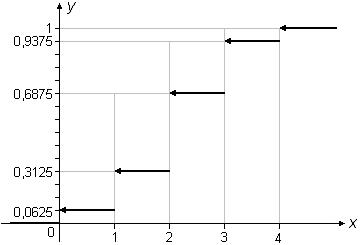
Рисунок 2.2. – График функции F(x)

Пример 2. Случайная величина Х задана интегральной функцией распределения:

Найти параметр а, плотность вероятности f(x), числовые характеристики М(Х), D(X), . Построить графики функций F(x), f(x).

Решение.

Найдем значение параметра а, используя свойство плотности вероятности:

Тогда функция плотности вероятности

Найдем числовые характеристики случайной величины Х:

Построим графики функций F(x) и f(x):

Рисунок 2.3. – График функции F(x)

Рисунок 2.4. – График функции f(x)

Вопросы для самоконтроля.

1. Что такое случайная величина?

2. Какие случайные величины являются дискретными, непрерывными?

3. Что такое закон распределения случайной величины?

4. Что такое (интегральная) функция распределения случайной величины?

5. Что такое плотность распределения вероятностей случайной величины?

6. Что называется кривой распределения случайной величины?

7. В чем заключается определение закона распределения дискретной случайной величины? Как составляется закон распределения?

8. Какие числовые характеристики имеет дискретная случайная величина? Дать определения.

9. Какие свойства имеет математическое ожидание?

10. Что такое дисперсия, среднее квадратическое отклонение? Какие свойства имеет дисперсия?

11. Математическое ожидание и дисперсия: случайной величины, распределенной по биномиальному закону и закону Пуассона.

12. Что такое функция распределения случайной величины?

13. Какими свойствами обладает функция распределения?

14. Что такое плотность распределения непрерывной случайной величины?

15. Какими свойствами обладает дифференциальная функция?

16. Какие числовые характеристики имеет непрерывная случайная величина?

Рекомендуемая литература: [1, 64-95], [2, c.52-79].

Вероятность того, что в n независимых испытаниях в каждом из которых событие А появляется с постоянной вероятностью р (0 2 ∙D(X);

Для дискретной случайной величины Х расчетная формула дисперсии:

для непрерывной величины:

Среднее квадратическое отклонениеслучайной величины Х равно корню квадратному из D(X): .

Пример 1. На пути движения автомобиля 4 светофора, каждый из которых с вероятностью р = 0,5 разрешает или запрещает движение автомобиля. Составить закон распределения величины Х – количества светофоров, которые автомобиль минует без остановки. Найти числовые характеристики М, D, величины Х, построить график F(x) и многоугольник распределения.

Решение. Возможные значения величины Х: 0, 1, 2, 3, 4. Вероятности этих значений найдем по формуле Бернулли при n = 4, p = 0,5 и q = 0,5.

Таким образом, закон распределения величины Х:

х_i	0	1	2	3	4
р_i	0,0625	0,25	0,375	0,25	0,0625

Найдем числовые характеристики дискретной случайной величины Х.

Построим многоугольник распределения:

Рисунок 2.1 – Многоугольник распределения

Построим функцию распределения F(x):

Рисунок 2.2. – График функции F(x)

Пример 2. Случайная величина Х задана интегральной функцией распределения:

Решение.

Найдем значение параметра а, используя свойство плотности вероятности:

Тогда функция плотности вероятности

Найдем числовые характеристики случайной величины Х:

Построим графики функций F(x) и f(x):

Рисунок 2.3. – График функции F(x)

Рисунок 2.4. – График функции f(x)

Вопросы для самоконтроля.

1. Что такое случайная величина?

2. Какие случайные величины являются дискретными, непрерывными?

3. Что такое закон распределения случайной величины?

4. Что такое (интегральная) функция распределения случайной величины?

5. Что такое плотность распределения вероятностей случайной величины?

6. Что называется кривой распределения случайной величины?

8. Какие числовые характеристики имеет дискретная случайная величина? Дать определения.

9. Какие свойства имеет математическое ожидание?

10. Что такое дисперсия, среднее квадратическое отклонение? Какие свойства имеет дисперсия?

Данная теорема является дальнейшим развитием схемы Бернулли и позволяет работать с диапазонами: какова вероятность, что число успехов будет лежать в пределах указанного отрезка.

. Пусть число испытаний $n$ достаточно велико, а вероятность успеха $0 \lt \,p\, \lt 1$. Пусть также$q=1-p$ — вероятность неудачного испытания. Тогда вероятность того, что число успехов будет лежать в пределах от $_>$ до $_>$, можно примерно посчитать по формуле:

\[_>\left( _>;_> \right)\approx \Phi \left( \frac<_>-np>> \right)-\Phi \left( \frac<_>-np>> \right)\]

где

\[\Phi \left( x \right)=\frac\!\!\pi\!\!\text< >>>\int\limits_^^^>>>>dt>\]

Функция $\Phi \left( x \right)$ называется функцией Лапласа и содержит в себе интеграл, который не считается напрямую. Как следствие, значения этой функции сведены в таблицу, которую можно загрузить прямо на этой странице.

\[\Phi \left( -x \right)=-\Phi \left( x \right)\]

Это прямо следует из определения, в котором присутствует определённый интеграл.

Что такое "интегральная теорема Муавра-Лапласса"?

Вероятность того, что при $n$-испытаниях количество успешных испытаний будет в пределах от $_>$ до $_>$ выражается следующей формулой:

Сама же функция $F$ называется функцией Муавра-Лапласа, и выглядит она следующим образом:

С $n$, я думаю, все понятно — это число испытаний.

$p$ — это вероятность успеха в каждом конкретном испытании.

$q$ — по аналогии с формулой Бернули это вероятность провала, т.е. неуспеха в каждом конкретносм испытании. Считатеся она по очень простой формуле:

Надеюсь, с буквами теперь понятно, поэтому перейдем к решению конкретных примеров.

Задача № 1

Начнем мы с довольно простой задачи, однако уже на ее примеры мы познакомимся с особенностями применения интегральной теоремы Муавра-Лапласса.

Известно, что в среднем 5% студентов носят очки. Какова вероятность того, что из 200 студентов, находящихся в аудитории, окажется не менее 10%, носящих очки?

В первую очередь, давайте запишем саму интегральную теорему Муавра-Лапласса:

При этом полезно помнить еще одну формулу:

Собственно, из-за этого интеграла, присутствуещего в функции Муавра-Лапласса, сама теорема и называется интегральной.

При первом взгляде на эту интегральную теорему многие ученики приходят в шок — уж больно много здесь разных конструкций, корней, вычислений и т.д. На самом деле, все очень просто, и сейчас вы сами в этом убедитесь.

Для начала давайте выпишем все значения. Итак, нам известно следующее:

Всего студентов 200 — $n=200$;
Вероятность попадания студента, который носит очки — $p=0,05$;
Вероятность того, что студенты не носят очки будет равна $1-0,05=0,95$.

Далее мы можем найти $\sqrt$:

Разумеется, такие вычисления выполняются на калькуляторе.

Кроме того, в нашей формуле, в интегральной теореме Муавра-Лапласса, мы наблюдаем выражение $np$ — произведение количества испытаний на вероятность успеха:

Давайте перепишем формулу с учетом всех фактов:

\[=F\left( 61,7 \right)-F\left( 3,25 \right)\]

И вот здесь нас поджидает первая проблема: если мы посмотрим на таблицу значений, то значение $3,25$ здесь еще присутствует, но вот числа от $60$ и более здесь вообще не представлены. Для решения этого вопроса предлагаю взглянуть на исходную формулу Муавра-Лапласса:

Итак, продолжим наше решение:

Нюансы решения

Как видите, ничего сверхъестественного. Все применение интегральной теоремы Муавра-Лапласса сводится к следующему:

Самое обидное, что именно такие чаще всего и попадаются на всяких контрольных, зачетах и экзаменах. Они будут вам встречаться на исследованиях, где необходимо определить какую-нибудь статистическую величину. Поэтому именно сейчас мы попытаемся решить такую задачу.

Задача № 2

Театр, вмещающий 1000 человек, имеет два разных входа, каждым из которых любой зритель может воспользоваться с равной вероятностью. Около каждого входа имеется свой гардероб. Сколько мест должно быть в каждом гардеробе, чтобы с вероятностью в 0,99 любой зритель смог раздеться в том гардеробе, в который он обратился сразу после входа в театр.

Я думаю, очевидно, что в данной задаче общее количество испытаний, т.е. человек, которые придут в театр, не более 1000 — $n=1000$.

Всего входов два, при этом в каждый с одинаковой вероятностью входит один и тот же человек — $p=\frac$.

Опять запишем интегральную теорему Муавра-Лапласса:

Подставим все полученные числа в формулу, с учетом того, что $_>=0$:

Теперь внимательно посмотрим на эту формулу. Отдельно посчитаем значение функции Муавра-Лапласса в следующей точке:

\[F\left( \frac \right)=-F\left( 31,6 \right)=0,5\]

Итого переписывая, мы получаем:

Единственный способ, при помощи которого можно решить этот пример — это взять таблицу значений функции Муавра-Лапласса и посмотреть, когда она равна $0,49$, при каком $x$. Проблема состоит в том, что точного значения мы не найдем. Однако есть значение функции Муавра-Лапласса в точках $2,32$ и $2,34$ :

\[F\left( 2,32 \right)=0,48983\]

\[F\left( 2,34 \right)=0,49036\]

Где-то между ними лежит наша искомая величина $0,49$. А между числами $2,32$ и $2,34$ лежит величина $2,33$. Так и запишем:

Теперь нам осталось решить простейшее уравнение:

Каверзные вопросы

Давайте для начала посмотрим на формулу функции Муавра-Лапласса:

Кроме того, в таблице значений все аргументы функций приведены именно в виде десятичных дробей, поэтому считая значение функции, мы просто обязаны перевести то, что стоит у нас внутри скобок, в десятичную дробь, в том числе с помощью калькулятора.

В заключение посмотрим еще одну задачку, в которой мы не только еще раз отработаем использование стандартной формулы, но и вспомним, что такое вторая версия теоремы Муавра-Лапласса, отличная от интегральной, и в каких ситуациях она применяется.

Задача № 3

Радиотелеграфная станция передает цифровой текст. В силу наличия помех каждая цифра независимо от других может быть неправильно принята с вероятностью 0,01. Найдите вероятность того, что в принятом тексте, содержащем 1100 цифр, будет:

б) менее 20 ошибок.

Решение пункта б)

Что касается б), то тут все вполне очевидно — это чистейшая теорема Муавра-Лапласса, причем интегральная. Так и запишем:

Теперь запишем интегральную формулу Муавра-Лапласса:

Осталось подставить числа в формулу:

\[=F\left( 2,42 \right)+F\left( 3,33 \right)=\]

Решение пункта а)

А теперь давайте разберемся с пунктом а). В нем от нас требуется, чтобы при тех же исходных данных, вычислить, что в итоге появится ровно 15 ошибок.

Очевидно, что это идеальная задача для применения второй версии теоремы Муавра-Лапласса — не интегральной. Давайте я ее запишу:\[\]

Выпишем известные данные:

\[_>\left( 15 \right)\approx \frac\cdot \varphi \left( \frac \right)\approx 0,303\cdot \varphi \left( 1,212 \right)\approx \]

\[\approx 0,303\cdot 0,1919\approx 0,058\]

Ключевые моменты

Вот и все, что я хотел вам рассказать об интегральной теореме Муавра-Лапласса, такой, на первый взгляд сложной, но очень простой на практике. Все, что вам необходимо — это

Знать сами формулы для обеих теорем Муавра-Лапласса, в том числе, интегральной.
Грамотно считать корни и элементы $np$, которые являются матожиданием.

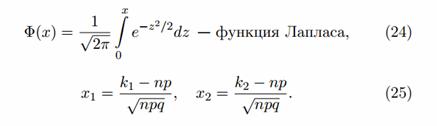
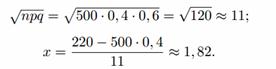
Пример №1 . В каждом из 500 независимых испытаний событие A происходит с постоянной вероятностью 0,4. Найдите вероятность того, что событие A происходит: а) ровно 220 раз; б) ровно 190 раз; в) меньше чем 240 и больше чем 180 раз; г) меньше чем 235 раз.
Решение. При решении этой задачи используем теоремы Лапласа: локальную в случаях а) и б) и интегральную для случаев в) и г).
а) Задано: n = 500, p = 0,4, k = 220.
Найдем P₅₀₀(220).
Имеем:
Значение функции φ(x) найдем из таблицы:

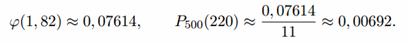
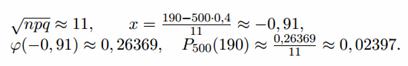
б) Задано: n = 500, p = 0,4, k = 190.
Найдем P₅₀₀(190).
Получаем:
в) Задано: n = 500, p = 0,4, a = 180, b = 240.
Найдем P₅₀₀(180 Пример №2 . В жилом доме имеется n ламп. Вероятность включения каждой из них в вечернее время равна 0.5. найти вероятность того, что число одновременно включенных ламп будет заключено между m₁ и m₂.

В том случае, когда количество манипуляций достаточно большое, применять формулу Бернулли становится нецелесообразно. Упростить решение задачи или доказательство выражения можно с помощью локальной и интегральной теорем Лапласа. Данные закономерности позволяют получить результат испытаний, приближенный к итогам вычислений по формуле Бернулли, и характеризуются меньшими расчетами.

Рассматриваемые теоремы активно применяют в решении задач по данным большого количества экспериментов для нахождения приближенного значения вероятности. С помощью локальной теоремы можно вычислить определенное число явлений. Благодаря интегральной теореме Муавра-Лапласа, достаточно просто найти ответ при заданном диапазоне вероятного количества возникновения событий.

Локальная теорема Лапласа

В том случае, когда вероятность p возникновения явления A характеризуется постоянством, и $p\ne 0$ и $p\ne 1$ , то вероятность $P_n ( k )$ того, что событие A возникнет k раз в n экспериментах, равна приближенно (увеличивая n, получаем более точный результат испытаний и меньше погрешность) значению функции $y=\frac < 1 > < \sqrt < n\cdot p\cdot q >> \cdot \frac < 1 > < \sqrt < 2\pi >> \cdot e^ < - < x^2 >/ 2 > =\frac < 1 > < \sqrt < n\cdot p\cdot q >> \cdot \varphi ( x )$

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Из выражения можно сделать вывод:

$label < eq2 >P_n ( k )\approx \frac < 1 > < \sqrt < n\cdot p\cdot q >> \cdot \varphi ( x )$

Следует отметить, что функция $\varphi ( x )=\varphi ( < -x >)$ является четной.

Свойства представленной функции:

функция является четной;
если аргумент обладает значением больше, чем 4, то функция будет сколь угодно мала.

Интегральная предельная теорема Муавра-Лапласа

Вероятность P, что возникнет событие A, для каждого эксперимента по порядку обладает стабильным значением, и $p\ne 0$ и $p\ne 1$ , тогда вероятность $P_n ( < k_1 ,k_2 >)$ того, что явление A наступит от $k_ < 1 >$ до $k_ < 2 >$ раз в n опытах, равна $P_n ( < k_1 ,k_2 >)\approx \frac < 1 > < \sqrt < 2\cdot \pi >> \int\limits_ < x_1 >^ < x_2 > < e^ < - < z^2 >/ 2 > dz > =\Phi ( < x_2 >)-\Phi ( < x_1 >)$

Следует отметить, что $\Phi ( x )=\frac < 1 > < \sqrt < 2\cdot \pi >> \int < e^ < - < z^2 >/ 2 > dz >$ можно определить с помощью специальных табличных схем.

$\Phi ( < -x >)=-\Phi ( x )$ является нечетной функцией.

Рассматриваемая функция обладает следующими основными свойствами:

функция является нечетной;
если аргумент больше, чем 5, то значение функции составляет 0,5.

Таблица значений для вычисления определителей

В случае применения локальной теории Лапласа целесообразно использовать специальные таблицы:

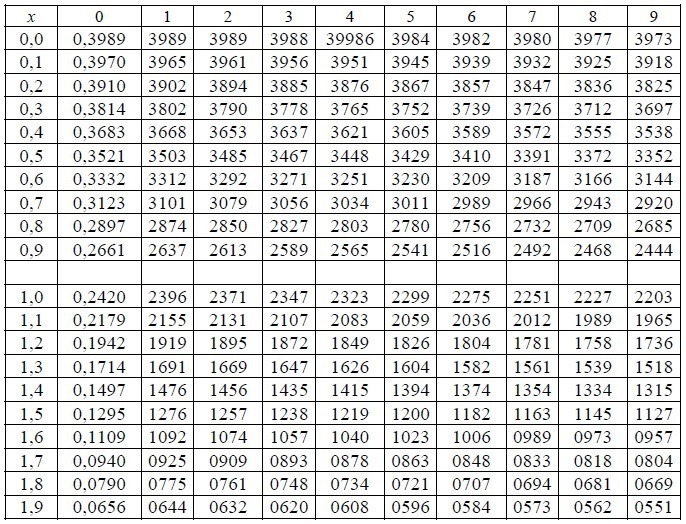
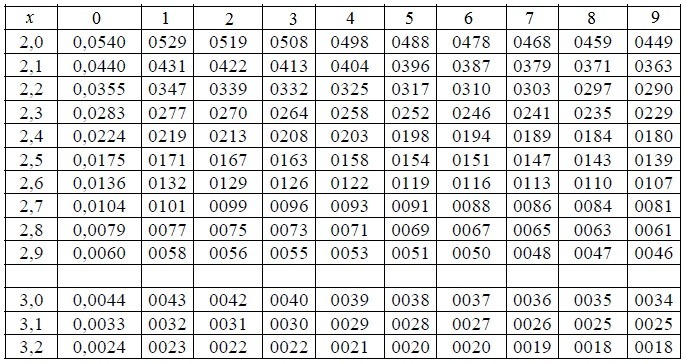
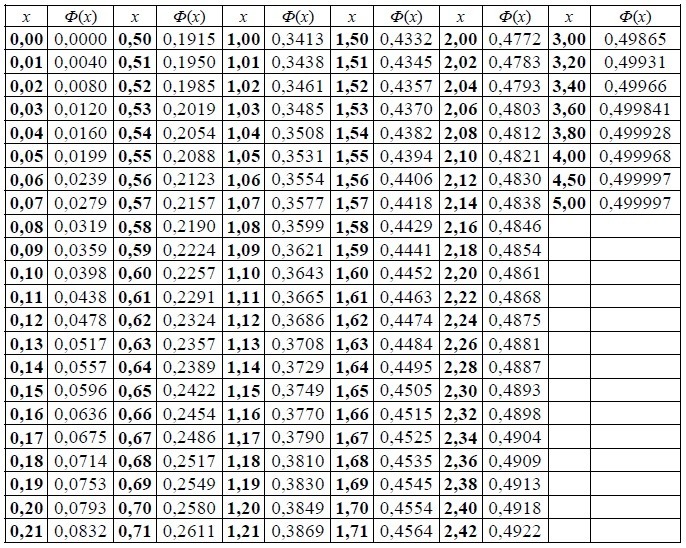
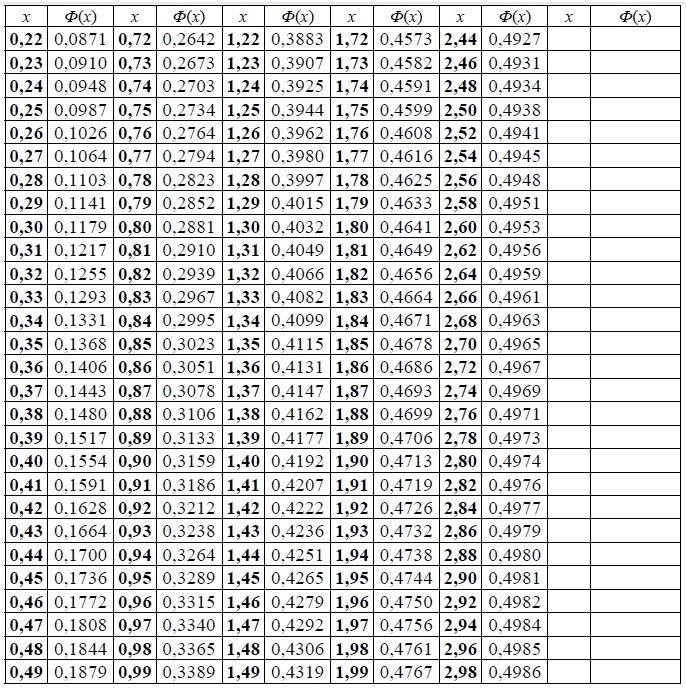
Таблица значений интегральной функции Лапласа имеет следующий вид:

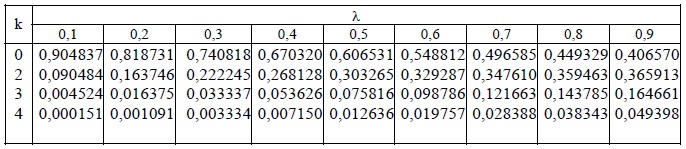
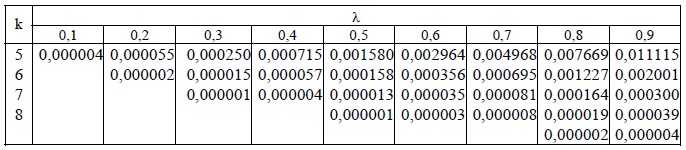
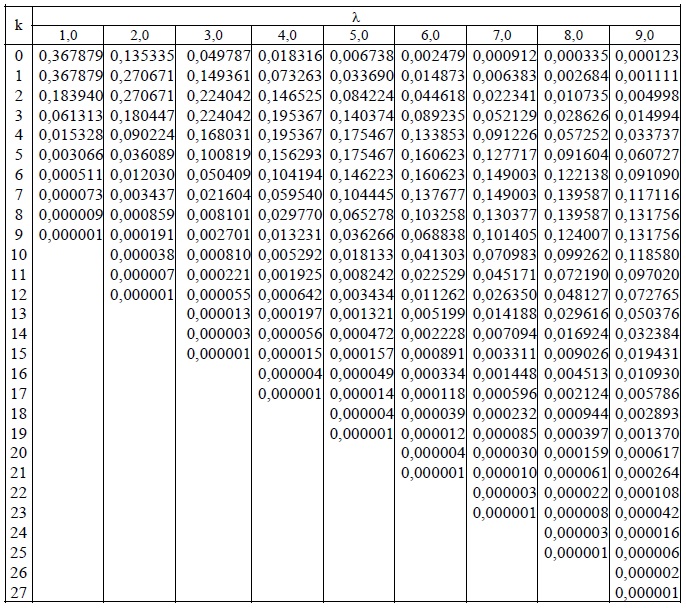
Применительно к вероятностям распределения Пуассона сформирована таблица:

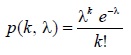
Пример решения задачи

Требуется определить, какова вероятность возникновения события А в течение 80 раз во время проведения 400 опытов. Следует учитывать вероятность появления данного события в каждом эксперименте составляет $ р = 0,2.$

В том случае, когда р = 0,2: q = 1 – p = 1 – 0,2 = 0,8

Ответ: вероятность равна 0,0498

По условиям задания, в процессе контроля качества выявляют 10% брака от произведенных изделий. Для этой процедуры выбирают 625 изделий. Необходимо определить вероятность того, что в объеме отобранных изделий имеется не меньше 550 и не больше 575 качественных экземпляров.

В том случае, когда брак составляет 10% от изделий, то качественные экземпляры должны определяться, как 90%. При таком условии:

Читайте также: