Формулы приведения кратко и понятно

Обновлено: 07.07.2024

Если аргументом тригонометрической функции является π 2 + t , π 2 − t , π + t , π − t , 3 π 2 + t , 3 π 2 − t , или в общем виде π n 2 ± t , где n ∈ ℤ , то такое выражение возможно привести к аргументу \(t\). Соответствующие формулы называют формулами приведения.

β	π 2 + t	π + t	3 π 2 + t	π 2 − t	π − t	3 π 2 − t	2 π − t
\(sin\) β	\(cos\)\(t\)	\(-sin\)\(t\)	\(-cos\)\(t\)	\(cos\)\(t\)	\(sin\)\(t\)	\(-cos\)\(t\)	\(-sin\)\(t\)
\(cos\) β	\(-sin\)\(t\)	\(-cos\)\(t\)	\(sin\)\(t\)	\(sin\)\(t\)	\(-cos\)\(t\)	\(-sin\)\(t\)	\(cos\)\(t\)
\(tg\) β	\(-ctg\)\(t\)	\(tg\)\(t\)	\(-ctg\)\(t\)	\(ctg\)\(t\)	\(-tg\)\(t\)	\(ctg\)\(t\)	\(-tg\)\(t\)
\(ctg\) β	\(-tg\)\(t\)	\(ctg\)\(t\)	\(-tg\)\(t\)	\(tg\)\(t\)	\(-ctg\)\(t\)	\(tg\)\(t\)	\(-ctg\)\(t\)

Существует очень много формул приведения. Таблицей пользоваться не всегда удобно. Запомнить их трудно — но самое главное, в этом нет необходимости. Достаточно запомнить одно-единственное правило — и легко можно самостоятельно выводить формулы и упрощать выражения.

1. Если аргумент исходной тригонометрической функции имеет вид π + t , π − t , 2 π + t , 2 π − t , то название функции оставляем прежним;

2. при аргументе исходной тригонометрической функции вида π 2 + t , π 2 − t , 3 π 2 + t , 3 π 2 − t название меняем на родственное;

3. полученная функция от аргумента \(t\) будет иметь такой знак, какой бы имела исходная функция при 0 t π 2 .

Данное правило применяют не только для аргумента, выраженного в радианах, но и в градусной мере для выражений вида 90 ° + t , 90 ° − t , 180 ° + t , 180 ° − t и т. д.

Формулы приведения разработаны для углов, представленных в одном из следующих видов: \(\frac<\pi>+a\), \(\frac<\pi>-a\), \(π+a\), \(π-a\), \(\frac<3\pi>+a\), \(\frac<3\pi>-a\), \(2π+a\) и \(2π-a\). Аналогично их можно использовать для углов представленных в градусах: \(90^°+a\), \(90^°-a\), \(180^°+a\), \(180^°-a\), \(270^°+a\), \(270^°-a\), \(180^°+a\), \(180^°-a\). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.

Как быстро получить любую формулу приведения

Для начала обратите внимание, что все формулы имеют похожий вид:

Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс или котангенс , он либо останется синусом, либо превратиться в косинус . А котангенс никогда не станет синусом или косинусом, он либо останется котангенсом, либо станет тангенсом. И так далее.

Едем дальше. Так как исходная функция и ее аргумент нам обычно даны, то весь вывод нужной формулы сводится к двум вопросам:
- как определить знак перед конечной функцией (плюс или минус)?
- как определить меняется ли функция на кофункцию или нет?

Как определить знак перед конечной функцией (плюс или минус)?

Какой знак был у исходной функции в исходной четверти, такой знак и нужно ставить перед конечной функцией.

Например, выводим формулу приведения для \(⁡cos⁡(\frac<3\pi>-a) =. \) С исходной функцией понятно – косинус, а исходная четверт ь ?

Для того, чтобы ответить на этот вопрос, представим, что \(a\) – угол от \(0\) до \(\frac<\pi>\), т.е. лежит в пределах \(0°…90^°\) (хотя это может быть не так, но для определения знака данная условность необходима). В какой четверти тригонометрической окружности при таком условии будет находиться точка, обозначающая угол \(\frac<3\pi>-a\)?
Чтобы ответить на вопрос, надо от точки, обозначающей \(\frac<3\pi>\), повернуть в отрицательную сторону на угол \(a\).

В какой четверти мы окажемся? В третьей. А какой же знак имеет косинус в третьей четверти? Минус. Поэтому перед итоговой функцией будет стоят минус: \(cos(\frac<3\pi>-a)=-. \)

А без приведения сложных аргументов тригонометрических функций к аргументам первой четверти на ЕГЭ по математике никуда.

Но нет необходимости учить эту таблицу !

Нужно просто потратить немного времени и понять алгоритм применения формул приведения.

Не будем терять время! Поехали!

Зачем вообще формулы приведения?

Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций к аргументам I четверти.

Вот, например, типичное задание из ЕГЭ по математике:

Давайте разбираться. А к примерам вернемся чуть позже.

Если хотите докапаться до самой сути, то –> + показать

Медленно, но верно. Далее сформулируем правило

Пример 1. Упростим .

Считаем – углом первой четверти!

Отмечаем значения и :

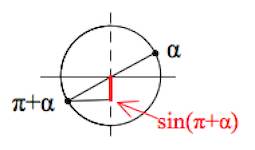
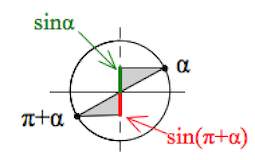
Но только – отрицательная величина, а – положительная.

Пример 2. Упростим .

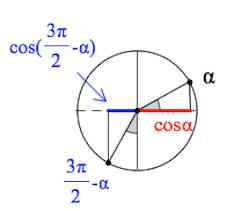
Из следующей картинки хорошо видно, что длина отрезка, помеченного синим цветом, равна длине отрезка, помеченного зеленым цветом.

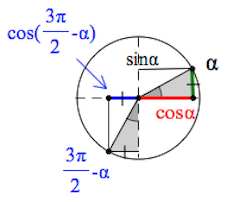
При этом – отрицательная величина, – положительная.

Пример 3. Упростим .

Значение же , как хорошо видно на картинке, то же, что и

Можно разбирать примеры и дальше для более четкого выявления закономерностей, но давайте уже сформулируем правило , на которое будем опираться при работе с формулами приведения .

Мнемоническое правило для формул приведения

Чтобы ответить на этот вопрос нужно, не смейтесь, – подвигать головой вдоль оси, на которой располагается ключевая точка. Ключевые точки всегда располагаются здесь (см. рис.):

Например, в формулах – ключевые точки – это .

2. Ставим справа, на выходе, тот знак, какой несет в себе левая, исходная, часть.

Примеры

Пример 1. Вычислить . + показать

Ключевая точка располагается на горизонтальной оси:

Название функции меняться не будет.

2. Исходное значение – отрицательно, так как располагается в IV четверти:

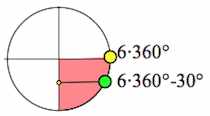
Пример 2. Вычислить + показать

Ключевая точка располагается на горизонтальной оси:

Название функции меняться не будет.

2. Исходное значение – отрицательно, так как располагается в III четверти:

Пример 3. Упростить + показать

(название меняем, проверять знак нет необходимости, так как все равно у нас функция – в квадрате)

Определение. Формулами приведения называют формулы, которые позволяют перейти от тригонометрических функций вида к функциям аргумента . С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.

Формулы приведения:

Для использования формул приведения существует два правила.

1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.

Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет

На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.

Пример:

Вычислить

Воспользуемся формулами приведения:

Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.

Читайте также: