Физический маятник это кратко

Обновлено: 05.07.2024

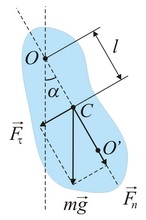
Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции. В положении равновесия центр инерции маятника С находится под точкой подвеса маятника O, на одной с ней вертикали (рис. 50). При отклонении маятника от положения равновесия на угол α возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

. (136)

(137)

Тогда для малых отклонений, когда выполняется условие sin(α) ≈ α, получаем уравнение гармонических колебаний:

. (138)

При малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, циклическая частота которых определяется формулой (137). Соответственно, период колебаний физического маятника равен:

. (139)

Из сопоставления формул (139) и (134) следует, что математический маятник с длиной

(140)

будет иметь такой период колебаний, как и данный физический маятник. Величину (140) называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см. точку О' на рис. 50).

По теореме Штейнера момент инерции маятника l может быть представлен в виде

где J₀ – момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маятника. Подставив (141) в формулу (140), получаем:

. (142)

Из (142) следует, что приведенная длина всегда больше l, так что точка подвеса и центр качания лежат по разные стороны от центра инерции.

Подвесим маятник в точке, совпадающей с центром качания О'. В соответствии с (142) приведенная длина в этом случае будет равна

(143)

где l' – расстояние между первоначальным центром качания и центром инерции маятника. Учитывая, что l' = L – l, выражение (143) можно записать следующим образом:

Поскольку J₀ + ml 2 равно моменту инерции относительно первоначальной оси вращения J, и этой же величине, согласно (140) равно выражение mlL, то числитель дроби будет равен нулю. Поэтому L' = L. Это означает, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

Это положение называется теоремой Гюйгенса:

. (136)

(137)

Тогда для малых отклонений, когда выполняется условие sin(α) ≈ α, получаем уравнение гармонических колебаний:

. (138)

. (139)

Из сопоставления формул (139) и (134) следует, что математический маятник с длиной

(140)

По теореме Штейнера момент инерции маятника l может быть представлен в виде

. (142)

(143)

Как выглядят колебания и период физического маятника. Узнайте про период колебаний, уравнение и формулу физического маятника, вращательный момент и инерцию.

Период у физического маятника находится в зависимости от момента инерции точки поворота и дистанции к центру масс.

Задача обучения

Вычислить параметры, воздействующие на период физического маятника.

Основные пункты

Физический маятник – обобщенный случай простого. Представлен любым твердым телом, осуществляющим колебания вокруг точки поворота.
В случае небольших амплитуд период основывается исключительно на моменте инерции вокруг точки поворота и дистанции от оси вращения к центру масс:
На период колебания маятника не влияет общая масса твердого объекта и массовое распределение. Изменение формы, размера и распределения массы повлияет на момент инерции и период.

Термины

Физический маятник – стержень или нить не лишены массы и способны увеличивать свой размер.
Массовое распределение – пространственное распределение и вычисление центра масс в объекте.

Физический маятник

Простой маятник представлен подвешенным грузом к безмассовой нити или стержню, лишенным трения. Здесь можно не учитывать эффекты от нити. А вот в физическом маятнике нить приобретает вес и способна растягиваться. Тогда период зависит от момента инерции вокруг точки поворота.

Мы видим, как силы влияют сквозь центр масс. Можно вычислить период маятника, выявив момент инерции вокруг точки поворота

Гравитация влияет сквозь центр масс твердого тела. Тогда длина маятника приравнивается к линейной дистанции между осью вращения и центром массы (h).

Уравнение вращательного момента:

τ = Iα (α – угловое ускорение, τ – вращательный момент, I – момент инерции).

Гравитация создает вращательный момент:

τ = mghsinθ (h – дистанция от центра масс к точке поворота, а θ – угол от вертикали).

То есть при небольшом угловом приближении:

Та же форма, что и у обычного простого маятника, где период:

И частота физического маятника:

Если мы располагаем моментом инерции, то можем вычислить период у физического маятника. Рассмотрим однородный стержень, повернутый из рамы. Центр масс расположен на дистанции L/2 от точки подвеса:

Жесткий стержень с равномерным распределением массы свисает с точки поворота. Это пример физического маятника

Момент инерции жесткого стержня вокруг его центра:

Также нужно выявить момент инерции относительно точки поворота, а не центра масс, поэтому применим теорему о параллельной оси:

Добавим результат к уравнению за период:

Только отметьте, что период физического маятника все еще зависит от массы. Зато лишен влияния массового распределения твердого тела. Перемены в форме, размере или распределении массы повлияют и на момент инерции, а это изменит период.

Дифференциальное уравнение движения физического маятника

Пренебрегая сопротивлением среды, дифференциальное уравнение качания физического маятника записывается следующим образом:

$<\displaystyle I<\frac <d^<2> \theta >>>=-mgh\sin \theta >$
.

$<\displaystyle <\frac <r^<2> Полагая >>+h=l>$
, предыдущее уравнение можно переписать в виде:

$<\displaystyle l<\frac <d^<2> \theta >>>=-g\sin \theta >$
.

$<\displaystyle l\,> Величина$
называется Центр качания физического маятника

Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.

Поместим на от точки подвеса. Эта точка и будет центром качания маятника.

$<\displaystyle I=ml^<2> Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен \,>$
, а момент силы тяжести относительно той же оси " width="" height="" />
. Легко заметить, что уравнение движения не изменится.

Теорема Гюйгенса

Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.

Доказательство

Вычислим приведенную длину для нового маятника:

$<\displaystyle l_<1> =>/h>>+>>=h+>>=l>$
.

Период колебаний физического маятника

$<\displaystyle <\frac <d^<2> Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на \theta >>>dt=d\left(>\right)>$
, а правую часть на " width="" height="" />
. Тогда:

$<\displaystyle l >d\left(>\right)=-g\sin \theta \,d\theta >$
.

Интегрируя это уравнение, получаем.

$<\displaystyle l\left(<\frac <d\theta > >\right)^=2g\cos \theta +C>$
,

где " width="" height="" />
произвольная постоянная. Её можно найти из граничного условия, что в моменты >=0>" width="" height="" />
. Получаем: " width="" height="" />
. Подставляем и преобразовываем получившееся уравнение:

$<\displaystyle <\frac <d\theta > >=2>>>-\sin ^>>>>$
.

Отделяем переменные и интегрируем это уравнеие:

$<\displaystyle <\sqrt <\frac <g> >>t=\int \limits _^<\frac <d\left(<\frac >\right)><\sqrt <\sin ^>-\sin ^<\frac >>>>>$
.

$<\displaystyle \sin <\frac <\theta > Удобно сделать замену переменной, полагая >=\sin >\sin \varphi >$
. Тогда искомое уравнение принимает вид:

$<\displaystyle t= >>\int \limits _^>\sin ^\varphi >>>=>>F\left(\varphi \setminus \alpha /2\right)>$
.

$<\displaystyle F\left(\varphi \setminus \alpha \right)> Здесь$
— .

$<\displaystyle K\left(\sin <\frac <\alpha > Здесь >\right)>$
- Период малых колебаний физического маятника

$<\displaystyle \alpha \,> Если амп$
мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:

$<\displaystyle T=2\pi <\sqrt <\frac <l> >>=2\pi >>>$
.

Отсюда видно, что физический маятник колеблется так же, как математический маятник с См. также

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Физический маятник. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

Воду из дока начинают выпускать так, что ее уровень равномерно падает, вследствие чего сила, действующая на шлюпку по вертикали вниз изменяется согласно закону, представленному на рис. Людмила Фирмаль

Активная сила-гравитация P- это потенциальная сила. Следовательно, обобщенная сила Q за счет потенциальной энергии выражается в виде Q = -dP / d h. Для доказательства теоремы мы применим теорему Штейнера к связи момента инерции относительно параллельной оси и физического маятника. Один из маятников проходит через центр тяжести. получить Jc, + Mh2 Mh (54) Поскольку отрезок OjC = JcJ (Mh) = l до h> 0, где JCz — момент инерции относительно горизонтальной оси, параллельной оси усиления и проходящей через центр тяжести. 2.

Центр маятника и опорная точка физического маятника взаимосвязаны. То есть, если такое же тело подвешено на горизонтальной оси, проходящей через центр качания, параллельной исходной оси, проходящей через точку поворота, длина предыдущего маятника, т.е. = /. Рассчитывает укороченную длину lt физического маятника оси. Здесь ось веса проходит через центр качания маятника до точки От-. Согласно теореме Штейнера, согласно сокращенному определению длины: , = 20 ° ^ = Jc, + M (1-Ky = JC, 1 Мтк Из (54) JCt = Mh (1 -h).

Если отрезок /, = / удален от точки Оi, вы получаете точку O. Другими словами, центр свинга и точка усиления взаимны. Период малых колебаний физического маятника вокруг горизонтальной оси, проходящей через точку усиления и центр качания, одинаков. Важное применение теории малых колебаний в физическом маятнике заключается в том, что ее можно использовать в качестве основы для экспериментального определения момента инерции объекта.

Если эти тела неподвижны, то скорости жидкости на их поверхности равны нулю, а следовательно, равны нулю касательные и нормальные по отношению к поверхности тел составляющие скоростей. Людмила Фирмаль

При экспериментальном определении момента инерции тела под действием силы тяжести P для любой оси эта ось является горизонтальной осью для увеличения веса, а также периодом колебаний малого тела вокруг этой оси и расстоянием от точки увеличения веса до центра тяжести. Достаточно решить. Далее, согласно (53), момент инерции относительно горизонтальной оси усиления равен (55)

Образовательный сайт для студентов и школьников

Читайте также: