Элементы алгебры логики 8 класс информатика кратко
Обновлено: 02.07.2024
Составил: учитель информатики Скрипкина Анна Анатольевна.
Тип урока: изучение нового материала
Цель урока: Ознакомление с понятием высказывания, с видами логических операций, формирование умений составлять логические выражения с помощью логических операций
Планируемые образовательные результаты:
Предметные: сформировать представление о алгебре логики, по знакомить с понятием высказывания, с простыми и сложными, истинными и ложными высказываниями, познакомить с логическими операциями.
Личностные: научить первичным навыкам анализа и критичной оценки получаемой информации, способствовать к готовности к общению и сотрудничеству со сверстниками
Метапредметные: способствовать овладению логическими действиями определения понятий,
Техническое обеспечение: компьютерный класс с персональными компьютерами, электронное приложение к учебнику Л.Л. Босова.
Организационный этап
Мотивационный момент
Учитель: Ребята, всем здравствуйте! Приготовились? Успокоились? (дети отвечают) Тогда потянулись и улыбнулись друг другу! Хорошо, можно присесть на свои места. Ребята, я вас прошу достать свои телефоны, там от меня увидите ссылку на опрос, всего один вопрос. (дети отвечают, учителю приходят результаты)
Учитель: Хорошо, всем спасибо! У кого плохое настроение, надеюсь в течение урока настроение изменится.

Объявление темы и целей урока
На экране картинка с задачей (слайд 2) . Учитель: ребятам давайте прочитаем задачу на экране и попробуем её решить. Кто-нибудь смелый нам поможет, поработает у доски. (Ребята рассуждают, учитель внимательно всё слушает. Просит кого-то из учеников выйти к доске и фиксировать ответы детей)
Через рассуждения ребята приходят к правильному ответу.
Учитель: Молодцы! Я сейчас подведу итог: эту задачу можно решить только с помощью размышления, рассуждения, логики. Ребята, из этого следует: какая у нас тема? (дети отвечают). (слайд 5)
Учитель: И так, ребята запишите в тетрадях тему нашего урока. (дети делают запись в тетрадях).
Учитель: Исходя из нашей темы, ребята, какую мы цель поставим себе на этот урок? (дети отвечают)
Учитель подводит итог: Ознакомление с понятием высказывания, с видами логических операций, формирование умений составлять логические выражения с помощью логических операций. (слайд 6)
Учитель: Ребята, теперь внимание на экран. Из предложенных задач какие мы выберем себе, для достижения нашей цели? (дети выбирают, учитель направляет) (слайд 7)
Актуализация опорных знаний
Понятие алгебры:
Учитель даёт основные понятия, дети записывают в тетрадях. (слайд 8)
Алгебра – это раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики; а в широком смысле этого слова – это наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разными математическими объектами.
Для информатики важен раздел, который называется алгеброй логики.
Алгебра логики или алгебра высказываний – это раздел математической логики, в котором изучаются логические операции над высказываниями.
Аристотель (384-322 до н.э.). - основоположник формальной логики (понятие, суждение, умозаключение).
Основоположником алгебры логики является Джордж Буль, он создал математическую логику или Булеву алгебру. (слайд 10)
Клод Шеннон (1916-2001). - его исследования позволили применить алгебру логики в вычислительной технике.
Учитель: Ребята, что такое высказывания? Давайте вспомним русский язык, литературу, что же такое высказывания? (дети отвечают, учитель подводит итог)
Учитель: Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно. Давайте посмотрим примеры. Ребята, побудительные предложения будут у нас высказываниями? А вопросительные? (дети отвечают)
Учитель: Но не всякое повествовательное предложение является высказыванием: Это высказывание ложное. Это предложение не будет являться логическим высказыванием. (слайд 11)
Учитель: Ребята, высказывания могут строиться с использованием знаков различных формальных языков – математики, физика, химии и т.д. (слайд 12)
Давайте приведем пример? 3+5=2*4 это истинное высказывание. (дети приводят примеры)
Учитель: Сейчас мы с вами разобьёмся на пары. Каждая пара получает листочек с заданием. Из предложенных предложений надо выбрать высказывание. Так приступаем к работе. (слайд 13)
Учитель: Итак, давайте проверим как вы поработали. (идёт проверка выбранных предложений, обсуждение) (слайд 14)
Учитель: Хорошо, все молодцы.
Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний.
В алгебре логики высказывания обозначают буквами и называют логическими переменными.
Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно - нулём (В = 0).
0 и 1 называются логическими значениями. (слайд 15)
Высказывания бывают простые и сложные. Высказывание называется простым, если никакая его часть сама не является высказыванием. Сложные (составные) высказывания строятся из простых с помощью логических операций. Посмотрите на экран, вот примеры простых предложений: Земля – планета Солнечной системы.
А сложным предложением будет: Если хочешь быть красивым, то поступи в гусары! (слайд 16-17)
На этом уроке мы с вами рассмотрим три основные логические операции, все они соответствуют связкам, употребляемым в естественном языке.
Учитель: сейчас мы с вами приступим к работе на компьютерах. (работа в электронном приложении к учебнику Босова.Л.)

Одним из направлений теоретической информатики является алгебра логики. Основы алгебры логики изучаются в школьном курсе информатики в 8 классе. Кратко об элементах алгебры логики можно прочитать в данной статье.
Элементы алгебры логики
Одним из разделов теоретической информатики является алгебра логики. Некоторые элементы алгебры логики доступны для понимания уже на школьном уровне.
Первые элементы алгебры логики были описаны в 19 веке в работах английского математика Джорджа Буля. Он первый высказал мысль о связи логики с математикой.
Высказывания
Не все предложения, несущие ту или иную информацию можно назвать высказываниями. Например, вопросительные или побудительные предложения – это не высказывания. Также не являются высказываниями математические выражения с переменными.
Например, не являются высказываниями следующие предложения:
- Сколько весит слон?
- Летайте самолетами Аэрофлота!
- 5*х + 8*y = 24
- Этот фильм самый лучший.
Алгебра логики изучает методы работы с высказываниями.
Действия над высказываниями
Высказывания как объекты могут быть операндами следующих логических действий
- Пересечение.
- Объединение.
- Инверсия.
Наглядно логические операции поясняют круги Эйлера или диаграммы Венна.
Пересечение
Пересечение – это действие над высказываниями, в результате которого будет получено новое высказывание истинное только в том случае, когда и исходные высказывания одновременно истинны.
Пересечение также называют логическим умножением, конъюнкцией или логическим И.
Обозначают знаками И, & или ∩.

Рис. 1. Диаграмма Венна для операции пересечения
На диаграмме операция пересечения выглядит как закрашенная область – представляющая собой общую для каждого операнда часть.
Объединение
Объединение – представляет собой действие над двумя высказываниями, в результате которого будет получено новое высказывание, ложное в том случае, когда одно из двух исходных операндов ложно.
Объединение также называют логическим сложением, дизъюнкцией, логическим ИЛИ.
Для ее обозначения используются знаки: ИЛИ, +, U.

Рис. 2. Диаграмма Венна для операции объединения
На диаграмме Венна операция объединения представляет собой всю область, относящуюся и к первому и ко второму операнду.
Инверсия
Инверсия – унарная логическая операция, заключающаяся в изменении на противоположное значение.
Инверсию обозначают знаками НЕ, ¬, ¯.
Инверсия на диаграмме Венна выглядит как область, не относящаяся к операнду.

Рис. 3. Диаграмма Венна для операции инвертирования
Аксиомы алгебры логики
В математике есть понятие аксиома – постулат, не требующий доказательств.
В математической логике также есть бездоказательные утверждения, касающиеся логических операций над высказываниями.
Для объединения справедливы аксиомы:
- А + 0 = А
- А + 1 = 1
- А + А = А
- А + НЕ(А) = 1
Для пересечения характерны такие аксиомы:
- А & 0 = 0
- А & 1 = А
- А & А = А
- А & НЕ(А) = О
Для операции инверсии применима аксиома двойного отрицания НЕ (НЕ (А)), когда дважды проинвертировав операнд получают в итоге само исходное значение.
Что мы узнали?
Алгебра логики стоит на стыке математики и информатики и составляет теоретическую базу, на основе которой строятся методы работы с информацией. Объектом изучения этого направления является высказывания. Основными логическими операциями являются пересечение, объединение и инверсия. В алгебре логики действуют ряд аксиом.
Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.
Что такое алгебра и алгебра логики
Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.

Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.
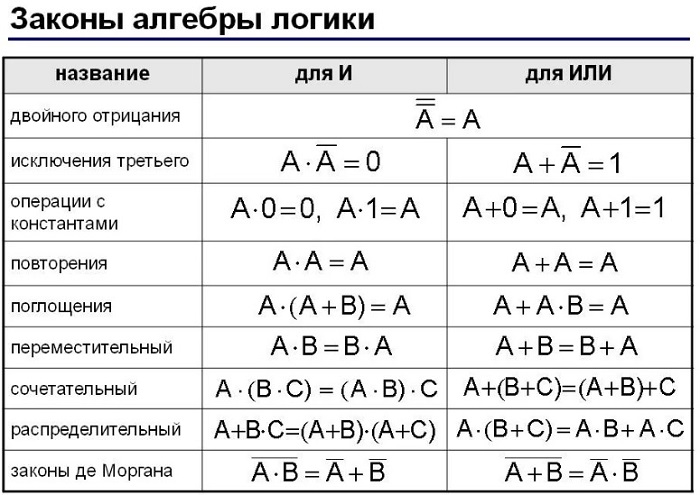
Законы алгебры логики
Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.

Переместительный закон - предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.
Сочетательный закон - применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.
Распределительный закон - имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.
Закон двойственности и инверсии (закон Моргана) - основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.
Основные законы алгебры логики представлены в таблице:
Логические выражения
В информатике предоставляется два вида высказываний: простое и сложное.

Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.
Нью-Йорк — столица США (ложное);
в России 1117 городов (верное).

Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.
Идёт дождь, а у меня нет зонта.
Основные логические операции
Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.
Логическое отрицание (инверсия) —НЕ
Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).
Таблица истинности инверсии:
Результаты операции НЕ следующие:
если исходное выражение истинно, то результат его отрицания будет ложным;
если исходное выражение ложно, то результат его отрицания будет истинным.
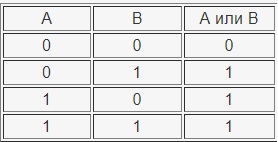
Логическое сложение (дизъюнкция, объединение) — ИЛИ
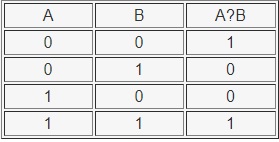
Таблица истинности операции ИЛИ:
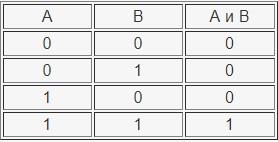
Логическое умножение(конъюнкция) — И
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.
За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).
При всех остальных значениях операция будет ложной.
Таблица истинности операции И приведена ниже:
Логическое следование (импликация) — ЕСЛИ ТО
Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.
Таблица истинности операции ЕСЛИ ТО выглядит так:
Операция эквивалентности (равнозначности) - А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.
И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.
Таблица истинности операции эквивалентности:

Все высказывания должны быть связаны между собой специальными элементами. В этом уроке рассказывается о таких логических операциях, как инверсия, конъюнкция и дизъюнкция. А также показывается, как правильно решать задачи с использованием этих операций.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Элементы алгебры логики. Логические операции"
На этом уроке мы с вами познакомимся с такими логическими операциями, как инверсия, конъюнкция и дизъюнкция. А также научимся решать задачи с использованием этих операций.
Мы с вами уже знаем, что высказывание – это предложение на любом языке, содержание которого можно однозначно определить, как истинное или ложное.
Высказывания бывают простыми и сложными.
Простое высказывание – это высказывание, в котором никакая его часть сама не является высказыванием.
К примерам простых высказываний можно отнести следующие предложения:


Первое простое высказывание истинно, а второе – ложно.
Сложные или же составные высказывания – это высказывания, которые строятся из простых с помощью логических операций.
Примером сложного высказывания будет следующее предложение:
А сейчас давайте узнаем, какие существуют основные логические операции. Для этого рассмотри таблицу.

В первом столбце у нас указаны названия логических операций, а во втором – логические связки.
Логическая связка – это союзы или выражения, которые употребляются в естественном языке для соединения простых высказываний в сложные.
Прежде чем приступить к рассмотрению всех логических операций, давайте рассмотрим таблицу, в которой указаны способы обозначения истинности и ложности логических высказываний. Существуют различные способы, но все они являются верными.

То есть мы можем написать просто словами на русском языке: Истинна или Ложь. Или же сократить их до первых букв. Также можно писать на английском языке: True или False. Или также сократить до первых букв. И последнее обозначение — это 1 и 0, где 1 – это истина, а 0 – ложь. Мы с вами будем использовать числа ноль и один.
А теперь давайте подробнее познакомимся с логическими операциями.
Давайте узнаем, как обозначается знак конъюнкции в различных сферах его применения.

А сейчас мы с вами составим таблицу истинности для конъюнкции.
Пусть у нас есть два высказывания А и B. Они будут заголовками первого и второго столбца. А новое выражение, которое образуется с помощью конъюнкции обозначим А и B – и это будет являться заголовком для третьего столбца.

Далее, вспомним, что если высказывание истинно, то ему соответствует число 1, а если ложно – 0.
Допустим, высказывания А и B – оба ложны. Занесём нули в соответствующие ячейки.

Из определения мы знаем, что новое высказывание будет истинно тогда и только тогда, когда истинны исходные высказывания. А так как у нас два высказывания ложны, значит и при их соединении мы получим новое ложное высказывание.

Далее, пусть А будет ложным, а B – истинным. Новое высказывание будет ложным, так как высказывание А – ложно.

Теперь сделаем наоборот, пусть А – истинно, B – ложно. И снова новое высказывание будет ложным.

А если высказывания А и B будут истинными, то новое высказывание также будет истинно. Так как в определение сказано, что новое высказывание будет истинно тогда и только тогда, когда истинны исходные высказывания.

Мы с вами рассмотрели все возможные значения исходных высказываний А и B.
Так же очень легко запомнить таблицу истинности для конъюнкции, если представить её в виде электрической цепи с двумя последовательными выключателями.

Лампочка загорится только в том случае, если два выключателя будут включены (замкнуты).

То есть тогда новое высказывание будет истинно.
Конъюнкцию также называют логическим умножением. Давайте посмотрим ещё раз на таблицу истинности.

Какие числа мы получим в результате перемножение первого и второго столбцов? В первых трёх строках третьего столбца будут нули, так как любое число при умножении на 0 даёт 0. А вот 1 на 1 равно 1. То есть мы получили такие же данные, как и при первом построении таблицы истинности.
А теперь переходим к дизъюнкции.
В различных сферах применения, дизъюнкция обозначается по-разному.

А теперь давайте составим таблицу истинности для дизъюнкции. Нам даны два высказывания А и B. Их значения мы будем вносить в первых два столбца. А в третий будем вносить обозначения, которые получаются при образовании нового высказывания с использованием дизъюнкции.

Итак, пусть наши два высказывания ложны. В определении сказано, что новое высказывание будет ложно тогда и только тогда, когда ложны два высказывания. Значит в нашем случае новое высказывание будет ложно.

Далее, пусть А будет ложным, а B – истинным. Новое высказывание будет истинным. Так как высказывание B – истинно.

Теперь сделаем наоборот, пусть А – истинно, B – ложно. И снова новое высказывание будет истинным.

А если высказывания А и B будут истинными, то новое высказывание снова будет истинно. Так как в определение сказано, что новое высказывание будет ложно тогда и только тогда, когда ложны исходные высказывания.

И снова для запоминания таблицы истинности можно использовать электрическую цепь с двумя параллельными выключателями.

То есть лампочка загорится в том случае если будет включён (замкнут), хотя бы один выключатель.


Дизъюнкцию ещё называют логическим сложением.

Давайте сложим данные из первого и второго столбцов. В результате мы получим такие же данные, как и при первом построении таблицы истинности. Обратим внимание на последнюю строку таблицы. При сложении двух логических единиц всё равно получается логическая единица. Алгебра логики оперирует только двумя значениями – ложью (логический ноль) и истиной (логическая единица). Истина не может быть двойной, тройной или истиной в квадрате, поэтому при сложении двух истин результатом будет просто истина, то есть цифра один.

И последняя логическая операция, которую мы с вами рассмотрим – это инверсия.
Здесь всё очень просто. Если исходное высказывание было истинно, то после инверсии оно становится ложным, а если исходное высказывание было ложным, то после операции инверсии оно становится истинным.
Давайте посмотрим, как обозначается инверсия в различных сферах её применения.

Нам осталось составить таблицу истинности для инверсии. Нам дано исходно высказывание А. Его значения будем записывать в первый столбик таблицы. А вот значение высказывания, которое получается после инверсии, будем записывать во второй столбик.

Итак, если наше высказывание А ложно, то новое высказывание будет истинно.

А если А – истинно, то новое высказывание после инверсии будет ложно.

Инверсию также называют логическим отрицанием.
Также любое сложное высказывание можно записать в виде логического выражения.
Логическое выражение – это выражение, которое содержит переменные, знаки логических операций и скобки.
Как и в математики, при выполнении логических операций в логическом выражении существует свой порядок действий. Сначала выполняется инверсия, затем конъюнкция, а после дизъюнкция. То есть, если записать все действия математическими знаками, то получим, что в начале выполняется действие отрицания (число меняется на противоположное), затем конъюнкция (умножение), а после всего дизъюнкция (сложение). Порядок выполнения действий можно изменять с помощью скобок.


А сейчас изобразим графически множества точек, для которых истины вышеприведённые выражения. Первое: НЕ А. То есть будет закрашено всё пространство, кроме круга А.

Во втором случае, А V B, будут закрашены два круга А и B.

А в третьем – всё пространство, кроме кругов А и B.

Данные изображения помогут нам решить задачу.

Это все точки, кроме тех, которые входят в круг А.
Второе: А V B. Смотрим на графическое представления для этого выражения.

Это все точки, которые входят в круги А и B. Для того, чтобы найти количество точек, давайте те точки, которые входят только в круг А обозначим буквой x, а которые входят только в B – буквой y. А точки, которые входят и в А и в Бэ обозначим буквой z. В круг А входят 190 точек, но в них есть точки z, которые входят и в А и в B.
Значит то наш x будет вычисляться следующим образом:
x = 190 – 70 = 120.
Аналогично и с кругом B, в который входят 230 точек.
y = 230 – 70 = 160.
Для того, чтобы вычислить точки, которые входят в А или B, нам нужно сделать следующее:
70 + 120 + 160 = 350.
То есть для 350 точек истинно выражения А V B.

Это все точки, которые не входят в круги А и B. Для их нахождения нужно:
Задача решена. И сейчас мы с вами подошли к подведению итогов урока.
Сегодня мы с вами узнали, что такое сложные высказывания, познакомились с такими логическими операциями, как конъюнкция, дизъюнкция и инверсия. Построили таблицы истинности для трёх логических операций, а также решили задачу с использованием кругов Эйлера и логических операций.
Читайте также:

