Доказательство теоремы косинусов кратко

Обновлено: 30.06.2024

Доказательство теоремы косинусов - не самое простое ( у теоремы синусов сильно проще), но смотря о каком доказательстве речь.

Чаще всего теорема доказывается через систему координат (у Л.С. Атанасян ) или через связку теорема Пифагора + соотношение между сторонами и углами прямоугольного треугольника . В обоих случаях - не самые короткие доказательства (особенно последнее, там вообще три типа треугольников рассматривается).

Рассмотрим другой способ, короткий и понятный. Через окружность.

Теорема

Квадрат стороны треугольника равен сумме квадратов других двух сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Доказательство

Рассмотрим произвольный треугольник, одна из вершин при большей стороне которого - центр окружности с радиусом равным этой большей стороне. И обозначим стороны этого треугольника, как показано на рисунке:

Через сторону c проведём еще один диаметр, а через сторону b достроим прямоугольный треугольник (в котором и найдём катет прилежащий к углу α ), так что получившийся диаметр и катет треугольника будут пересекаться в некоторой точке. А значит, по свойству пересекающихся хорд :

Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.

Теорема косинусов:

Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:

Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Следствие из теоремы косинусов.

Теорема косинусов используется для определения cos угла треугольника:

h 2 = a 2 - (c – b cos α) 2 (2)

Приравниваем правые части уравнений (1) и (2):

b 2 - (b cos α) 2 = a 2 - (c - b cos α) 2

a 2 = b 2 + c 2 - 2bc cos α.

Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Теорема 1 (теорема косинусов). Квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

То есть для любого треугольника ABC со сторонами a, b, c справедливо равенство:

Доказательство. Пусть задан треугольник ABC. Проведем высоту h из вершины C на сторону c=AB (Рис.1).

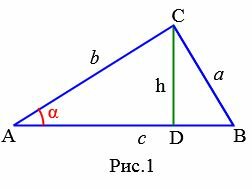Теорема Пифагора для прямоугольных треугольников ADC и CDB имеет вид:

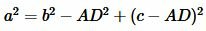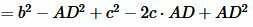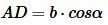
Учитывая, что: , получим:

Доказательство (по векторам). Пусть задан треугольник ABC. Представим вектор AC в виде суммы векторов AB и BC (Рис.2).

где − скалярное произведение векторов и .

Используя дистрибутивность скалярного произведения векторов относительно сложения и коммутативность скалярного произведения векторов уравнение (5) можно преобразовать так:

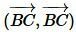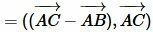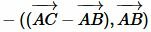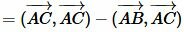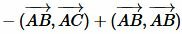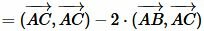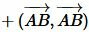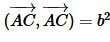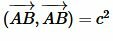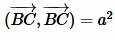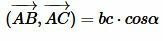Примеры и решения

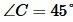
Задание 1. В треугольнике ABC, a=16, b=10, угол между ними . Найти сторону c.

Решение. Из теоремы косинусов, имеем:

Подставляя значения сторон a, b и угла C в (6), получим:

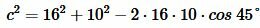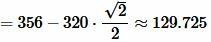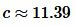
Ответ: .

Задание 2. В треугольнике ABC, a=8, b=14, c=12. Найти углы α, β, γ (Рис.3).

Представь себе, это такая… теорема Пифагора для произвольного треугольника. Она однажды тебя спасёт!

Дальше смотри рисунки и ты все поймешь. Один рисунок лучше тысячи слов 🙂

Разберёшься в ней – будь уверен, что любая задача с треугольником окажется тебе под силу!

Теорема косинусов — коротко о главном

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

Почему теорема косинусов это… теорема Пифагора

И причем тут теорема Пифагора? Сейчас поясню.

Согласно теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.

А что будет, если угол \( \displaystyle \angle C\), скажем, острый?

Вроде ясно, что величина \( \displaystyle ^>\) должна быть меньше, чем \( \displaystyle <^>+^>\). Но вот на сколько меньше?

А если угол \( \displaystyle \angle C\) – тупой?

Ну, тогда величина \( \displaystyle ^>\) больше, чем \( \displaystyle <^>+^>\)?

Но, опять же, на сколько? И как это связано с величиной \( \displaystyle \angle C\)?

Доказательство теоремы косинусов

Итак, для всякого (и остроугольного, и тупоугольного и даже прямоугольного!) треугольника верна теорема косинусов.

Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

Рассмотрим три случая:

угол С острый,
угол С тупой,
угол С прямой.

И убедимся, что для всех трех случаев теорема косинусов работает!

Угол С острый

\( \displaystyle \angle C

Он прямоугольный, можно пользоваться теоремой Пифагора:

Что такое \( \displaystyle AH\) и \( \displaystyle HB\) ?

\( \displaystyle AH\) можно выразить из треугольника (прямоугольного!) \( \displaystyle AHC\).

\( \displaystyle AH=b\sin \gamma \)

А вот \( \displaystyle BH=a-CH=a-b\cos \gamma \) (снова из \( \displaystyle \Delta AHC\) ).

Читать далее…

Мы хотим постоянно улучшать этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)

Угол С тупой

Начинаем точно также: опускаем высоту из точки \( \displaystyle A\).

А теперь, внимание, отличие!

\( \displaystyle AH=b\sin \left( ^>-\gamma \right)\) — это из \( \displaystyle \Delta AHC\) , который теперь оказался снаружи \( \displaystyle \Delta ABC\), а

\( \displaystyle BH=a+b\cos \left( ^>-\gamma \right)\).

Читать далее…

Угол С прямой

Но тогда \( \displaystyle \cos \gamma =0\) и теорема косинусов просто превращается в теорему Пифагора:

В каких же задачах бывает полезна теорема косинусов?

Ну, например, если у тебя даны две стороны треугольника и угол между ними, то ты прямо сразу можешь найти третью сторону.

Или, если тебе даны все три стороны, то ты тут же найдешь косинус любого угла по формуле:

И даже, если тебе даны две стороны и угол НЕ между ними, то третью сторону тоже можно найти, решая квадратное уравнение. Правда, в этом случае получается иногда два ответа и нужно соображать, какой же из них выбрать, или оставить оба.

Попробуй применять и не бояться – теорема косинусов почти также легка в обращении, как и теорема Пифагора.

И приходи к нам на бесплатные вебинары и занятия ( о них ниже).

Бонус: Вебинар на решение задач по теореме косинусов и синусов

Теорема косинусов (и синусов) — универсальный инструмент при решении треугольников — это теоремы косинусов и синусов.

А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.

Этот вебинар из нашего курса подготовки к ЕГЭ по математике (о нем ниже). Вы выучите сами теоремы и научитесь применять их при решении задач первой части.

Читайте также: