Доказательство площади квадрата кратко и понятно

Обновлено: 05.07.2024

Начнем с того случая, когда a = 1/n, где n является целым числом.
Возьмем квадрат со стороной 1 и разобьем его на n 2 равных квадратов так, как показано на рисунке 1.

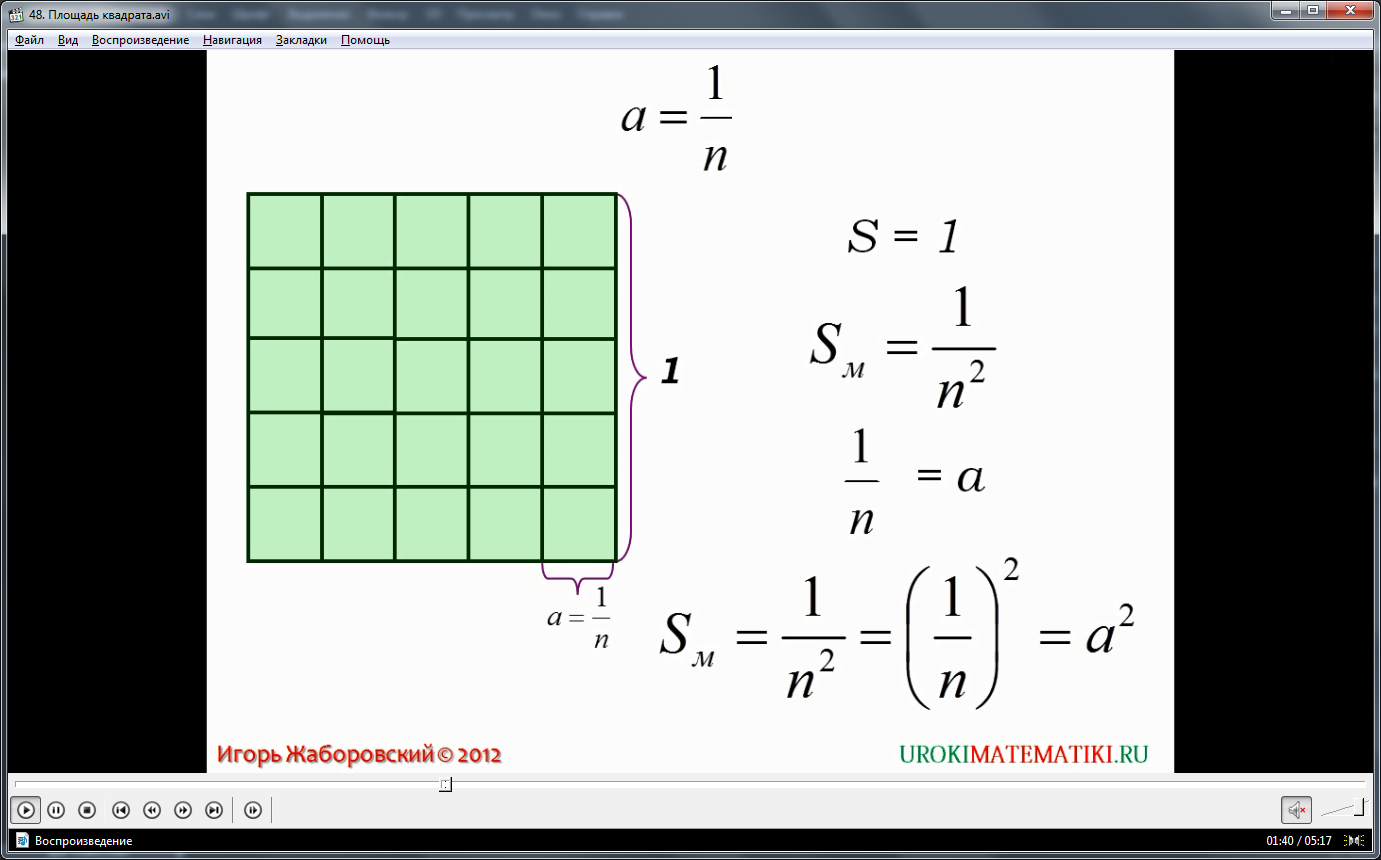
Так как площадь большого квадрата равна единице, то площадь каждого маленького квадрата равна 1/n 2 . Сторона каждого маленького квадрата равна 1/n, т. е. равна a. Итак,
S = 1/n 2 = (1/n) 2 = a 2 . (1)
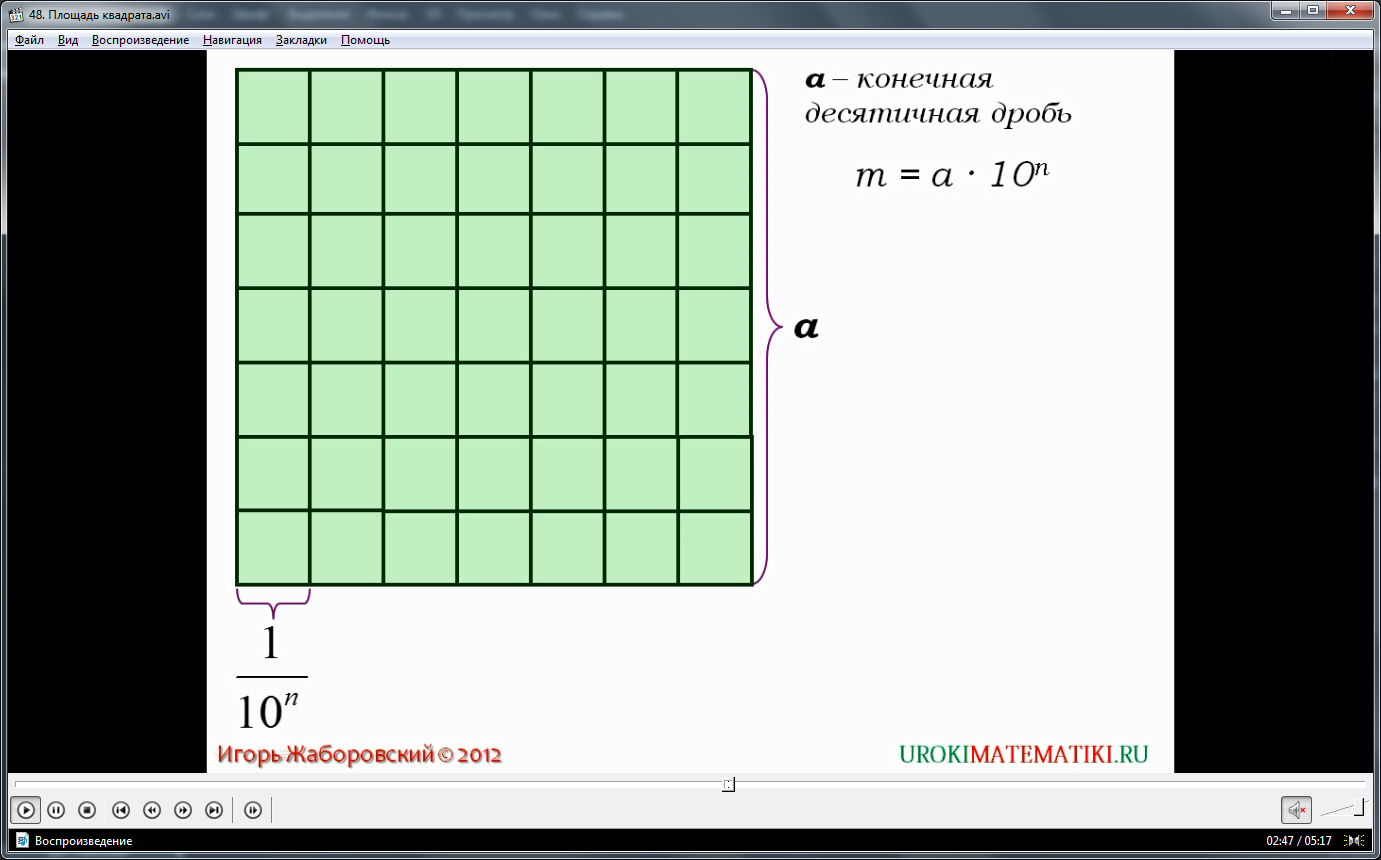
Пусть теперь число a представляет собой конечную десятичную дробь, содержащую n знаков после запятой (в частности, число a может бать целым, и тогда n = 0). Тогда число m = a · 10 n целое. Разобьем данный квадрат со стороной a на m 2 равных квадратов так, как показано на рисунке 2.

При этом каждая сторона данного квадрата разобьется на m равных частей, и, значит, сторона любого маленького квадрата равна

a/m = a / (a · 10 n ) = 1/10 n .

По формуле (1) площадь маленького квадрата равна (1/10 n ) 2 . Следовательно, площадь S данного квадрата равна

m 2 · (1/10 n ) 2 = (m/10 n ) 2 = ((a · 10 n )/10 n ) 2 = a 2 .

Наконец, пусть число a представляет собой бесконечную десятичную дробь. Рассмотрим число a_n, получаемое из a отбрасыванием всех десятичных знаков после запятой, начиная с (n + 1)-го. Так как число a отличается от a_n не более чем на 1/10 n , то a_n ≤ a ≤ a_n + 1/10 n , откуда

a_n 2 ≤ a 2 ≤ (a_n + 1/10 n ) 2 . (2)

Ясно, что площадь S данного квадрата заключена между площадью квадрата со стороной a_n и площадью квадрата со стороной a_n + 1/10 n :

т. е. между a_n 2 и (a_n + 1/10 n ) 2 :

a_n 2 ≤ S ≤ (a_n + 1/10 n ) 2 . (3)

Будем неограниченно увеличивать число n. Тогда число 1/10 n будет становиться сколь угодно малым, и, значит, число (a_n + 1/10 n ) 2 будет сколь угодно мало отличаться от числа a_n 2 . Поэтому из неравенств (2) и (3) следует, что число S сколь угодно мало отличается от числа a 2 . Следовательно, эти числа равны: S = a 2 , что и требовалось доказать.

Так же площадь квадрата можно найти с помощью следующих формул:

S = 4r 2 ,
S = 2R 2 ,

где r — радиус вписанной в квадрат окружности,
R — радиус описанной вокруг квадрата окружности.

Площадь квадрата – это численная характеристика, характеризующая размер плоскости, ограниченной четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами равен 90 градусов.

Для вычисления площади квадрата применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь или проверить уже выполненные вычисления.

Площадь квадрата через его сторону

Площадь квадрата через его диагональ

Площадь квадрата через периметр

Площадь квадрата через отрезок проведенный из вершины квадрата к середине противоположной стороны

Площадь квадрата через радиус вписанной окружности

Площадь квадрата через радиус описанной окружности

Таблица с формулами площади квадрата

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	сторона
2	диагональ
3	периметр
4	отрезок проведенный из вершины квадрата к середине противоположной стороны
5	радиус вписанной окружности
6	радиус описанной окружности

Определения

Квадрат – это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами равен 90 градусов.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.

Квадрат часто называют правильным четырехугольником, потому что его углы и стороны равны. Давайте разберемся, какие формулы помогут найти его площадь, чтобы решать задачи быстро и легко.

О чем эта статья:

3 класс, 8 класс

Формула нахождения площади квадрата

Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.

Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат.

S = a × a = a 2 , где S — площадь, a — сторона.

Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.

Если нам дана диагональ

Возводим ее в квадрат и делим на два.

S = d 2 : 2, где d — диагональ.

Если известен радиус вписанной окружности

Умножаем его квадрат на четыре.

S = 4 × r 2 , где r — это радиус вписанной окружности.

Если у нас есть радиус описанной окружности

Возведем его в квадрат и умножим на два.

S = 2 × R 2 , где R — это радиус описанной окружности.

У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!

Если есть периметр

Мы должны возвести его в квадрат и разделить на 16.

S = Р 2 : 16, где Р — это периметр.

Периметр любого четырехугольника равен сумме длин всех его сторон.

Задачку не решить, если длина и ширина даны в разных единицах. Для правильного решения переведите все данные к одной единице измерения, и все получится.

Популярные единицы измерения площади:

квадратный миллиметр (мм 2 );
квадратный сантиметр (см 2 );
квадратный дециметр (дм 2 );
квадратный метр (м 2 );
квадратный километр (км 2 );
гектар (га).

S квадрата. Решение задач

Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!

Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.

Воспользуемся формулой: S = d 2 : 2.

Подставим в формулу значение диагонали: S = 90 2 : 2 = 4050 мм 2 .

Ответ: 4050 мм 2 .

Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.

Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d

Диаметр окружности равен двум радиусам:
d = 2r

Получается, что сторона равна двум радиусам:
a = 2r

Используем формулу нахождения площади квадрата через сторону:
S = a 2

Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2

Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2

От множества геометрических фигур квадрат отличается тем, что является правильным четырехугольником с равными углами и равными сторонами. Если выразить сторону квадрата каким-нибудь числом, то можно найти площадь квадрата. Она численно равна квадрату его стороны.

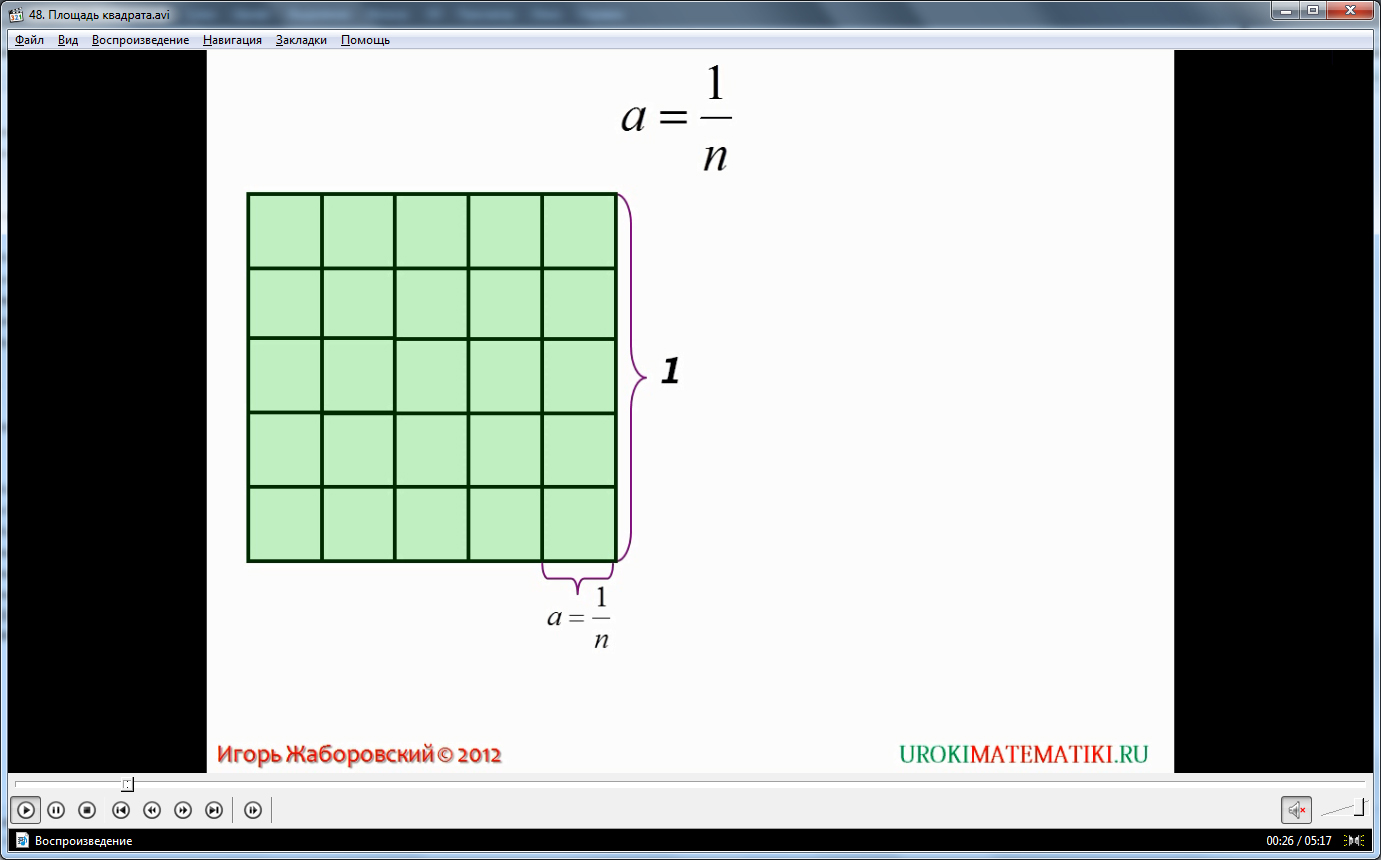
Доказательство этого положения приведено в данном видео уроке. На первом слайде показан квадрат. Его сторона принята равной единице. Следовательно, площадь квадрата тоже равна единице. Стороны квадрата разбиты одинаковые отрезки. На каждой стороне помещается одинаковое, причем целое, число отрезков. Это число в общем случае равно n. Итак, n – целое число. Если соединить отрезки, как показано на рисунке видео урока, квадрат окажется разделенным на маленькие квадраты. Всего их будет n 2 . В видео уроке сторона малого квадрата обозначена как a. Значит, ее длина равна 1/n, площадь же малого квадрата оказывается равной 1/n 2 . Площадь малого квадрата обозначена S_м. Поскольку дробь 1/n 2 = (1/n) 2 , то можно записать, что S_м = (1/n) 2 . Но поскольку 1/n = a, можно записать, что S_м = a 2 .

Итак, был рассмотрен случай, когда n является целым числом.

Следующий слайд видео урока объясняет случай, когда сторона квадрата a выражена конечной десятичной дробью. У этой дроби имеется после запятой n знаков. Стороны квадрата, показанного на слайде, разбиты на целое число равных отрезков. Это число обозначено m, и оно равно m = a х 10 n . Сам же квадрат на слайде разбит также на целое число равных малых квадратов. Всего этих малых квадратов получается m 2 . Сторона каждого такого маленького квадрата равна числу a, деленному на число m.

Математическая запись будет выглядеть так:

a/m = a/a х 10 n = 1/10 n . Значит, длина стороны маленького квадрата равна 1/10 n . Так и показано на слайде видеоурока.

Согласно тому, что было записано выше, площадь маленького квадрата должна равняться квадрату его стороны. На слайде видеоурока эта площадь найдена и записана так:

S_м = (1/ 10 n ) 2 . Но поскольку большой квадрат изначально был разбит на m 2 равных частей, то общая площадь его, S, будет равна сумме площадей маленьких квадратов. Как известно, операцию сложения, если слагаемые одинаковы, можно заменить операцией умножения, и записать так:

S = m 2 х (1/ 10 n ) 2 = (m х 1/ 10 n ) 2 = (a х 10 n /10 n ) 2 = a 2 .

Итак, в видеоматериале доказано, что если сторона квадрата выражена числом, представляющем собой конечную десятичную дробь, площадь этого квадрата будет определена квадратом этой стороны.

На последнем слайде этого видео урока рассматривается случай, когда сторона квадрата a выражена бесконечной десятичной дробью. Здесь предлагается рассмотреть некоторое число a_n, которое получится, если у числа a после запятой отбросить все десятичные знаки, начиная с n+1-го знака. Соотношение между числами a, a_n и a_n+1/10 n записано в видеоматериале с помощью двойного неравенства.

Все части этого неравенства можно возвести в квадрат, тогда получается, что площадь исходного квадрата, S, больше, чем площадь квадрата со стороной a_n, и меньше, чем площадь квадрата со стороной a_n+1/10 n . Это числовое неравенство на слайде проиллюстрировано с помощью рисунка. Если теперь бесконечно увеличивать число n, число 1/10 n будет неограниченно уменьшаться и, в конце концов, мало отличаться от нуля. Из записанных неравенств видно, что число S при бесконечном увеличении числа n будет равно a 2 , что и требовалось доказать.

Читайте также: