Дисперсия дискретной случайной величины кратко

Обновлено: 04.07.2024

Дисперсия - это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая - значения сравнительно близки друг к другу, если большая - далеки друг от друга (см. примеры нахождения дисперсии ниже).

Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии - среднеквадратическое отклонение $\sigma(X)=\sqrt$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.

Еще одно формальное определение дисперсии звучит так: "Дисперсия - это второй центральный момент случайной величины" (напомним, что первый начальный момент - это как раз математическое ожидание).

Формула дисперсии случайной величины

Дисперсия случайной величины Х вычисляется по следующей формуле: $$ D(X)=M(X-M(X))^2, $$ которую также часто записывают в более удобном для расчетов виде: $$ D(X)=M(X^2)-(M(X))^2. $$

Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид: $$ D(X)=\sum_^-\left(\sum_^ \right)^2. $$ Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом: $$ D(X)=\int_<-\infty>^ <+\infty>f(x) \cdot x^2 dx - \left( \int_<-\infty>^ <+\infty>f(x) \cdot x dx \right)^2. $$

Пример нахождения дисперсии

Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.

Пример 1. Вычислить и сравнить дисперсию двух законов распределения: $$ x_i \quad 1 \quad 2 \\ p_i \quad 0.5 \quad 0.5 $$ и $$ y_i \quad -10 \quad 10 \\ p_i \quad 0.5 \quad 0.5 $$

Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором - дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии: $$ D(X)=\sum_^-\left(\sum_^ \right)^2 =\\ = 1^2\cdot 0.5 + 2^2 \cdot 0.5 - (1\cdot 0.5 + 2\cdot 0.5)^2=2.5-1.5^2=0.25. $$ $$ D(Y)=\sum_^-\left(\sum_^ \right)^2 =\\ = (-10)^2\cdot 0.5 + 10^2 \cdot 0.5 - (-10\cdot 0.5 + 10\cdot 0.5)^2=100-0^2=100. $$ Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $\sigma(X)=0.5$, $\sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором - на 10 единиц от среднего 0.

Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).

Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения: $$ x_i \quad -1 \quad 2 \quad 5 \quad 10 \quad 20 \\ p_i \quad 0.1 \quad 0.2 \quad 0.3 \quad 0.3 \quad 0.1 $$

Снова используем формулу для дисперсии дискретной случайной величины: $$ D(X)=M(X^2)-(M(X))^2. $$ В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание: $$ M(X)=\sum_^ =-1\cdot 0.1 + 2 \cdot 0.2 +5\cdot 0.3 +10\cdot 0.3+20\cdot 0.1=6.8. $$ Потом математическое ожидание квадрата случайной величины: $$ M(X^2)=\sum_^ = (-1)^2\cdot 0.1 + 2^2 \cdot 0.2 +5^2\cdot 0.3 +10^2\cdot 0.3+20^2\cdot 0.1=78.4. $$ А потом подставим все в формулу для дисперсии: $$ D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16. $$ Дисперсия равна 32.16 квадратных единиц.

Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x \in(0,6)$ и $f(x)=0$ в остальных точках.

Вычисление дисперсии онлайн

Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.

Введите число значений случайной величины К.
Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
Нажмите на кнопку "Вычислить".
Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.

Видео. Полезные ссылки

Видеоролики: что такое дисперсия и как найти дисперсию

Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Полезные ссылки

Что еще может пригодиться? Например, для изучения основ теории вероятностей - онлайн учебник по ТВ. Для закрепления материала - еще примеры решений задач по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

Итак, продолжаем. В предыдущей статье мы выяснили, насколько полезно знать математическое ожидание, однако только этой характеристики ещё не достаточно для исследования случайной величины. Представим двух стрелков, которые стреляют по мишени. Один стреляет метко и попадает близко к центру, а другой… просто развлекается и даже не целится. Но что забавно, его средний результат будет точно таким же, как и у первого стрелка! Эту ситуацию условно иллюстрируют следующие случайные величины:

Таким образом, возникает потребность количественно оценить, насколько далеко рассеяны пули (значения случайной величины) относительно центра мишени (математического ожидания). Ну а рассеяние с латыни переводится не иначе, как дисперсия.

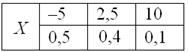
Посмотрим, как определяется эта числовая характеристика на одном из примеров 1-й части урока:

Там мы нашли неутешительное математическое ожидание этой игры, и сейчас нам предстоит вычислить её дисперсию, которая обозначается через .

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

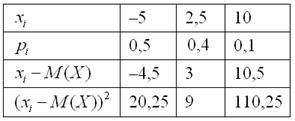
Чтобы обойти эту неприятность можно рассмотреть модули разностей, но по техническим причинам прижился подход, когда их возводят в квадрат. Решение удобнее оформить таблицей:

И здесь напрашивается вычислить средневзвешенное значение квадратов отклонений. А это ЧТО такое? Это их математическое ожидание, которое и является мерилом рассеяния:

– определение дисперсии. Из определения сразу понятно, что дисперсия не может быть отрицательной – возьмите на заметку для практики!

Иногда это значение называют стандартным отклонением.

В чём его смысл? Если мы отклонимся от математического ожидания влево и вправо на среднее квадратическое отклонение:

Во-первых, очевидно то, что при увеличении ставок, дисперсия тоже возрастает. Так, например, если мы увеличим в 10 раз, то математическое ожидание увеличится в 10 раз, а дисперсия – в 100 раз (коль скоро, это квадратичная величина). Но, заметьте, что сами-то правила игры не изменились! Изменились лишь ставки, грубо говоря, раньше мы ставили 10 рублей, теперь 100.

Второй, более интересный момент состоит в том, что дисперсия характеризует стиль игры. Мысленно зафиксируем игровые ставки на каком-то определённом уровне, и посмотрим, что здесь к чему:

То же самое происходит на Форексе, других биржах и так далее – примеров масса.

Наверное, вы заметили, что нахождение дисперсии – есть процесс длительный и кропотливый. Но математика щедрА:

Формула для нахождения дисперсии

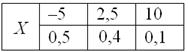
Данная формула выводится непосредственно из определения дисперсии, и мы незамедлительно пускаем её в оборот. Скопирую сверху табличку с нашей игрой:

и найденное матожидание .

Вычислим дисперсию вторым способом. Сначала найдём математическое ожидание – квадрата случайной величины . По определению математического ожидания:

В данном случае:

Таким образом, по формуле:

Как говорится, почувствуйте разницу. И на практике, конечно, лучше применять формулу (если иного не требует условие).

Осваиваем технику решения и оформления:

Дискретная случайная величина задана своим законом распределения:

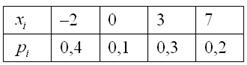
Найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.

Эта задача встречается повсеместно, и, как правило, идёт без содержательного смысла.
Можете представлять себе несколько лампочек с числами, которые загораются в ~~дурдоме~~ с определёнными вероятностями :)

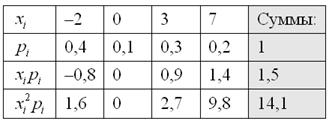
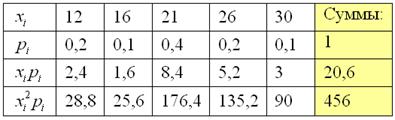
Решение: Основные вычисления удобно свести в таблицу. Сначала в верхние две строки записываем исходные данные. Затем рассчитываем произведения , затем и, наконец, суммы в правом столбце:

Собственно, почти всё готово. В третьей строке нарисовалось готовенькое математическое ожидание: .

Дисперсию вычислим по формуле:

И, наконец, среднее квадратическое отклонение:
– лично я обычно округляю до 2 знаков после запятой.

Все вычисления можно провести на калькуляторе, а ещё лучше – в Экселе:

вот здесь уже трудно ошибиться :)

Ответ:

Желающие могут ещё более упростить свою жизнь и воспользоваться моим калькулятором (демо), который не только моментально решит данную задачу, но и построит тематические графики (скоро дойдём). Программа доступна за символическую плaтy. Спасибо за поддержку проекта!

Пара заданий для самостоятельного решения:

Вычислить дисперсию случайной величины предыдущего примера по определению.

И аналогичный пример:

Дискретная случайная величина задана своим законом распределения:

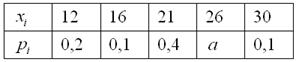
Да, значения случайной величины бывают достаточно большими (пример из реальной работы), и здесь по возможности используйте Эксель. Как, кстати, и в Примере 7 – это быстрее, надёжнее и приятнее.

Решения и ответы внизу страницы.

В заключение 2-й части урока разберём ещё одну типовую задачу, можно даже сказать, небольшой ребус:

Дискретная случайная величина может принимать только два значения: и , причём . Известна вероятность , математическое ожидание и дисперсия .

Решение: начнём с неизвестной вероятности. Так как случайная величина может принять только два значения, то сумма вероятностей соответствующих событий:

и поскольку , то .

Осталось найти …, легко сказать :) Но да ладно, понеслось. По определению математического ожидания:
– подставляем известные величины:

– и больше из этого уравнения ничего не выжать, разве что можно переписать его в привычном направлении:

ОК, едем дальше. По формуле вычисления дисперсии:
– подставляем известные данные:

О дальнейших действиях, думаю, вы догадываетесь. Составим и решим систему:

Десятичные дроби – это, конечно, полное безобразие; умножаем оба уравнения на 10:

Вот так-то лучше. Из 1-го уравнения выражаем:
(это более простой путь) – подставляем во 2-е уравнение:

Возводим в квадрат и проводим упрощения:

В результате получено квадратное уравнение, находим его дискриминант:
– отлично!

и у нас получается два решения:

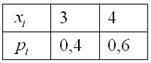
Условию удовлетворяет первая пара значений. С высокой вероятностью всё правильно, но, тем не менее, запишем закон распределения:

и выполним проверку, а именно, найдём матожидание:

В результате получены исходные значения, что и требовалось проверить.

Ответ:

Следует отметить, что это технически трудное задание, и поэтому в нём следует проявлять повышенное внимание. Потренируйтесь самостоятельно:

Случайная величина принимает только два значения: и , причём . Найти эти значения, если .

Тут вычисления попроще.

Жду вас в третьей, заключительной части урока, где мы познакомимся с многоугольником и функцией распределения. Её лучше изучить как можно скорее!

Решения и ответы:

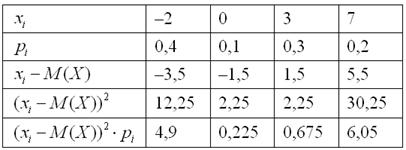
Пример 7. Решение: вычислим математическое ожидание:

Вычислим дисперсию по определению:
Заполним расчётную таблицу:

Таким образом:

Пример 8. Решение: случайная величина может принять только 5 значений, поэтому:

Заполним расчётную таблицу:

Математическое ожидание: .
Дисперсию вычислим по формуле:

Среднее квадратическое отклонение:

Пример 10. Решение: т.к. случайная величина может принимать только 2 значения, то:
.
По определению математического ожидания:

По формуле вычисления дисперсии:

Составим и решим систему:

Умножим оба уравнения на 5:

Из первого уравнения выразим: – подставим во второе:

Решим полученное квадратное уравнение:

Условию удовлетворяет первая пара.

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Что такое дисперсия в статистике

Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.

Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.

Характеристики равномерного распределения представлены на картинке:

При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.

Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.

Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.

Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.

Виды дисперсии дискретной случайной величины

Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.

Общая дисперсия

Простая дисперсия, без разделения на группы:

Или в несколько преобразованном виде:

Взвешенная дисперсия, для вариационного ряда:

где x_i – значение из ряда;

f_i – частота, количество повторений;

n – число вариантов.

Черта сверху указывает на среднюю величину.

Межгрупповая дисперсия

Как найти данную дисперсию? По формуле:

где k – количество групп;

n_j – элементов в группе с индексом j.

Внутригрупповая дисперсия

Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.

В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.

Если вычислить среднюю величину от всех групповых,

то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.

Взаимосвязь

В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.

Свойства дисперсии

Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.

Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ 2 можно по отклонениям от фиксированного числа.

Уменьшение всех цифр в k раз приведет к падению D[X] в k 2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.

Средний квадрат отклонений от постоянной величины X отличается в большую сторону от того же с использованием среднего значения. Разница составит (X_c_р – X) 2 .

Показатели вариаций

Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:

Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.

Пример расчета дисперсии

Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.

По альтернативной формуле:

Заключение

Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.

Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.

Математическое ожидание не дает полной характеристики закона распределения случайной величины.

Покажем это на примере с решением:

Пусть заданы две дискретные случайные величины и своими законами распределения:

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Вот еще один пример:

При одинаковой средней величине годовых осадков одна местность может быть засушливой и неблагоприятной для сельскохозяйственных работ (нет дождей весной и летом), а другая — благоприятной для ведения сельского хозяйства.

Пусть задана дискретная случайная величина

Определение 1. Отклонением случайной величины от ее Математического ожидания (или просто отклонением случайной величины назывется случайная величина

Видно, что для того, чтобы отклонение случайной величины приняло значение достаточно, чтобы случайная величина приняла значение Вероятность же этого события равна следовательно, и вероятность того, что отклонение случайной величины примет значение также равна Аналогично обстоит дело и для остальных возможных значений отклонения случайной величины Используя это, запишем закон распределения отклонения случайной величины

Вычислим теперь отклонения Пользуясь свойствами 5 и 1 (§2.1, п. 2), получим

Следовательно, справедлива следующая теорема.

Теорема. Математическое ожидание отклонения равно нулю:

Из теоремы видно, что с помощью отклонения не удается определить среднее отклонение возможных значений величины от ее математического ожидания, т.е. оценить степень рассеяния величины Это объясняется взаимным погашением положительных и отрицательных возможных значений отклонения. Однако можно освободиться от этого недостатка, если рассматривать квадрат отклонения случайной величины

Возможно вам будут полезны данные страницы:

Запишем закон распределения случайной величины (рассуждения те же, что и в случае случайной величины

Определение 2. Дисперсией дискретной случайной величины называется математическое отклонение квадрата отклонения случайной величины от ее математического отклонения (среднего значения):

Из закона распределения величины следует, что

Пример:

Пусть случайная величина задана своим законом распределения:

Найдем Имеем:

Таким образом, закон распределения случайной величины выразится таблицей:

Свойства дисперсии дискретной случайной величины

1. Дисперсия дискретной случайной величины равна разности между математическим ожиданием квадрата величины и квадратом ее математического ожидания:

Действительно, используя свойства математического ожидания, имеем:

С помощью этого свойства и свойств математического ожидания Устанавливаются и другие свойства.

2. Дисперсия постоянной величины равна нулю. Действительно,

3. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

4. Дисперсия суммы двух независимых случайных величин и равна сумме дисперсий этих величин:

Используя метод математической индукции, это свойство можно распространить и на случай любого конечного числа слагаемых.

Следствием свойств 3 и 4 является следующее свойство.

5. Дисперсия разности двух независимых случайных величин и равна сумме их дисперсий:

Примеры с решением

Пример 1.

Используя свойство 1 дисперсии, найдем дисперсию случайной величины имеющей следующий закон распределения:

Находим математические ожидания случайной величины и ее квадрата:

Отсюда в силу свойства 1 дисперсии

Пример 2.

Дисперсия случайной величины равна 3. Найдем дисперсию следующих величин:

Согласно свойствам 2, 3 и 4 дисперсии, имеем:

Примечание. Если множество возможных значений дискретной случайной величины бесконечно, то ее дисперсия определяется суммой сходящегося числового ряда

Биномиальное распределение

Пусть осуществляется испытаний, причем вероятность появления события в каждом испытании равна и не зависит от исхода других испытаний (независимые испытания). Такая последовательность испытаний называется схемой Бернулли*. Так как вероятность наступления события в одном испытании равна то вероятность его ненаступления равна

Найдем вероятность того, что при испытаниях событие наступит раз

Пусть событие наступило в первых испытаниях раз и не наступило во всех последующих испытаниях. Это сложное событие можно записать в виде произведения:

Общее число сложных событий, в которых событие наступает раз, равно числу сочетаний из элементов по элементов. При этом вероятность каждого сложного события оказывается равной Так как указанные сложные события являются несовместимыми, то вероятность их суммы равна сумме их вероятностей. Итак, если есть вероятность появления события раз в испытаниях, то

Формула (2.6) называется формулой Бернулли.

Пример 3.

Пусть всхожесть семян данного растения составляет 90%. Найдем вероятность того, что из четырех посеянных семян взойдут: а) три; б) не менее трех.

а) В данном случае

Применяя формулу Бернулли, получим

б) Искомое событие состоит в том, что из четырех семян взойдут или три, или четыре. По теореме сложения вероятностей Но Поэтому

Снова рассмотрим независимых испытаний, в каждом из которых наступает событие с вероятностью Обозначим через случайную величину, равную числу появлений события в испытаниях.

Понятно, что событие может вообще не наступить, наступить 1 раз, 2 раза и т. д. и, наконец, наступить раз. Следовательно, возможными значениями величины будут числа

По формуле Бернулли можно найти вероятности этих значений:

Запишем полученные данные в виде таблицы распределения:

Построенный закон распределения дискретной случайной величины называется законом биномиального распределения.

Найдем для биноминального распределения. Очевидно, что — число появлений события в каждом испытании — представляет собой случайную величину со следующим распределением:

Поэтому Но так как

Найдем далее Так как величина имеет распределение

то Поэтому

Наконец, в силу независимости величин

Отсюда для биноминального распределения

Пример 4.

Монета брошена 2 раза. Напишем в виде таблицы закон распределения случайной величины — числа выпадений герба. Вероятность появления герба в каждом бросании монеты

Следовательно, вероятность непоявления герба При двух бросаниях монеты герб может либо совсем не появиться, либо появиться 1 раз, либо появиться 2 раза. Таким образом, возможные значения таковы: Найдем вероятность этих возможных значений по формуле Бернулли:

Тогда искомый закон распределения будет иметь вид:

Пример 5.

На основании формулы Бернулли (2.6) для вероятности появления события в серии ровно раз имеет место формула

Пусть фиксировано. Тогда (здесь использован второй замечательный предел

Если велико, то в силу определения предела вероятность сколь угодно мало отличается от Отсюда при больших

для искомой вероятности имеем приближенную формулу Пуассона (для простоты знак приближенного равенства опущен).

Где

Пример 6.

Завод отправил на базу 500 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,002. Найдем вероятность того, что на базу придут три негодных изделия.

По условию Поэтому и искомая вероятность

Определение. Говорят, что случайная величина распределена по закону Пуассона, если эта величина задана таблицей

где — фиксированное положительное число (разным значениям отвечают разные распределения Пуассона).

Полезно проверить, что для приведенной таблицы сумма всех вероятностей равна единице. Действительно, с учетом известного разложения для имеем

Распределение Пуассона заслуживает особого внимания, так как из всех дискретных распределений оно наиболее часто встречается в приложениях.

Найдем математическое ожидание дискретной величины распределенной по закону Пуассона. Согласно определению математического ожидания (§ 2.2, п. 2, примечание 2), имеем

Таким образом, параметр в распределении Пуассона есть не что иное, как математическое ожидание величины

Найдем далее Сначала найдем начальный момент второго порядка (§ 2.3, п. 4):

Читайте также: