Деление отрезка в данном отношении кратко
Обновлено: 05.07.2024
Разделить отрезок в данном отношении это значит найти на заданном отрезке такую точку М, для которой имеет место равенство
Пусть точки имеют соответственно координаты Найдем координаты х, у точки М. Обозначим через проекции точек на ось (рис. 8). Из элементарной геометрии известно, что отрезки, заключенные между параллельными прямыми, пропорциональны. Следовательно,
Но поэтому . В этом отношении модули можно заменить разностями , если учесть, что эти разности имеют одинаковые знаки (см. рис. 8, а, на котором обе разности положительны, и рис. 8, б, на котором они отрицательны). Таким образом,
Аналогично можно получить соответствующее выражение и для у.
Окончательно, для координат х и у искомой точки М получим следующие формулы:
В частности, для координат середины отрезка получим формулы:
Таким образом, каждая из координат середины отрезка равна среднему арифметическому соответствующих координат его концов.
Пример. Разделить отрезок в отношении если
Решение. Так как , то по формулам (4) получим:
Таким образом, искомой оказалась точка
Замечание. При решении задачи о делении отрезка в данном отношении мы предполагали, что этот отрезок - направленный, т. е. имеющий начало М, и конец . Если сохранить численное значение , а точки поменять местами, то точка М, делящая отрезок в отношении , не будет, вообще говоря, совпадать с прежней точкой М, делившей в отношении отрезок .
Например, точкой, делящей в отношении отрезок имеющий начало и конец будет уже не точка , а точка , координаты которой находятся следующим образом:
Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.
Определение координат точки, делящей отрезок в заданном отношении, на плоскости
Исходные данные: задана прямоугольная система координат O x y и две лежащие на ней, несовпадающие точки с заданными координатами A ( x A , y A ) и B ( x B , y B ) . А также задана точка С , делящая отрезок А В в отношении λ (некоторое положительное действительное число). Необходимо определить координаты точки С : x C и y C .
В этом случае точка А – начало отрезка, точка В – конец отрезка. Если бы было задано, что точка С делит в заданном отношении отрезок В А , тогда верным было бы равенство: .
Ну и совсем очевидный факт, что если λ = 1 , то точка С является серединой отрезка А В .
Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки А , В и точку С на отрезке А В . Построим радиус-векторы указанных точек, а также векторы A C → и C B → . Согласно условиям задачи, точка С делит отрезок А В в отношении λ .

Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) и O B → = ( x B , y B ) .
Определим координаты вектора : они будут равны координатам точки С , которые и требуется найти по условию задачи.
Используя операцию сложения векторов, запишем равенства: O C → = O A → + A C → O B → = O C → + C B → ⇔ C B → = O B → - O C →
По условию задачи точка С делит отрезок А В в отношении λ , т.е. верно равенство A C = λ · C B .
Векторы A C → и C B → лежат на одной прямой и являются сонаправленными. λ > 0 по условию задачи, тогда, согласно операции умножения вектора на число, получим: A C → = λ · C B → .
Преобразуем выражение, подставив в него : C B → = O B → - O C → .
A C → = λ · ( O B → - O C → ) .
Равенство O C → = O A → + A C → перепишем как O C → = O A → + λ · ( O B → - O C → ) .
Используя свойства операций над векторами, из последнего равенства следует: O C → = 1 1 + λ · ( O A → + λ · O B → ) .
Теперь нам остается непосредственно вычислить координаты вектора O C → = 1 1 + λ · O A → + λ · O B → .
Выполним необходимые действия над векторами O A → и O B → .
O A → = ( x A , y A ) и O B → = ( x B , y B ) , тогда O A → + λ · O B → = ( x A + λ · x B , y A + λ · y B ) .
Таким образом, O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ ) .
Резюмируя: координаты точки С , делящей отрезок А В в заданном отношении λ определяются по формулам : x C = x A + λ · x B 1 + λ и y C = у A + λ · y B 1 + λ .
Определение координат точки, делящей отрезок в заданном отношении, в пространстве
Исходные данные: прямоугольная система координат O x y z , точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) .
Точка С делит отрезок А В в отношении λ . Необходимо определить координаты точки С .
Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:
O C → = 1 1 + λ · ( O A → + λ · O B → )
Векторы и являются радиус-векторами точек А и В , а значит:
O A → = ( x A , y A , z A ) и O B → = ( x B , y B , z B ) , следовательно
O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )
Таким образом, точка С , делящая отрезок А В в пространстве в заданном отношении λ , имеет координаты: ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )
Рассмотрим теорию на конкретных примерах.
Исходные данные: точка С делит отрезок А В в отношении пять к трем. Координаты точек А и В заданы A ( 11 , 1 , 0 ) , B ( - 9 , 2 , - 4 ) .
Решение
По условию задачи λ = 5 3 . Применим полученные выше формулы и получим:
x A + λ · x B 1 + λ = 11 + 5 3 · ( - 9 ) 1 + 5 3 = - 3 2
y A + λ · y B 1 + λ = 1 + 5 3 · 2 1 + 5 3 = 13 8
z A + λ · z B 1 + λ = 0 + 5 3 · ( - 4 ) 1 + 5 3 = - 5 2
Ответ: C ( - 3 2 , 13 8 , - 5 2 )
Исходные данные: необходимо определить координаты центра тяжести треугольника А В С .
Заданы координаты его вершин: A ( 2 , 3 , 1 ) , B ( 4 , 1 , - 2 ) , C ( - 5 , - 4 , 8 )
Решение
Известно, что центром тяжести любого треугольника является точка пересечения его медиан (пусть это будет точка М ). Каждая из медиан делится точкой М в отношении 2 к 1 , считая от вершины. Исходя из этого, найдем ответ на поставленный вопрос.
Допустим, что А D – медиана треугольника А В С . Точка М – точка пересечения медиан, имеет координаты M ( x M , y M , z M ) и является центром тяжести треугольника. М , как точка пересечения медиан, делит отрезок А D в отношении 2 к 1 , т.е. λ = 2 .
Найдем координаты точки D . Так как A D – медиана, то точка D – середина отрезка В С . Тогда, используя формулу нахождения координат середины отрезка, получим:
x D = x B + x C 2 = 4 + ( - 5 ) 2 = - 1 2 y D = y B + y C 2 = 1 + ( - 4 ) 2 = - 3 2 z D = z B + z C 2 = - 2 + 8 2 = 3
Требуется разделить отрезок АВ, соединяющий точки и , в заданном отношении , т.е. найти координаты точки отрезка АВ такой, что (рис. 3).
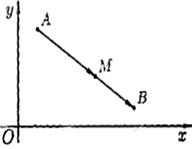
Для нахождения координат точки используют
Формулы (2) называются формулами деления отрезка в данном отношении. В частности, при λ = 1, т. е. если AM = MB, то они примут вид , . В этом случае точка М(х;у) является серединой отрезка АВ.
Пропорцию можно составить и в другом порядке: – сия запись означает, что отрезок в два раза длиннее отрезка , но какого-то принципиального значения для решения задач это не имеет. Можно так, а можно так.

Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:
Здесь справедливо соотношение: . Если составить пропорцию наоборот, тогда получаем: .
Формулы деления отрезка в данном отношении:
Если известны две точки плоскости , то координаты точки , которая делит отрезок в отношении , выражаются формулами:
В пространственном случае и добавляется дополнительная координата:
.
Откуда взялись данные формулы? В курсе аналитической геометрии эти формулы выводятся с помощью векторов (куда ж теперь без них? =)).
Задача 11
Найти координаты точки , делящей отрезок в отношении , если известны точки
Решение: по умолчанию, отсчёт начинается от первого конца отрезка: . По формулам деления отрезка в данном отношении, найдём точку :
Ответ:
Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате чего часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от многоэтажности дроби (см. Приложение Школьные материалы) и проводим окончательные упрощения.
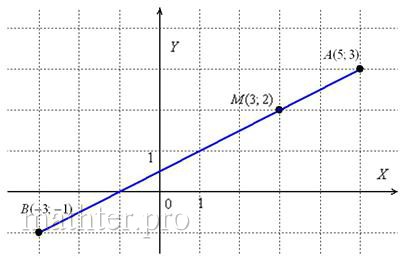
В задаче не требуется строить чертежа, но его полезно выполнить на черновике:
– чтобы убедиться в том, что соотношение действительно выполнено, то есть отрезок в три раза короче отрезка . Если длины не очевидны, то отрезки всегда можно тупо измерить обычной линейкой.
Существует и второй способ решения: в нём отсчёт начинается с точки и справедливым является отношение: (иными словами, отрезок в три раза длиннее отрезка ). По формулам деления отрезка в данном отношении:
Ответ:
Задача 12
а) Точка принадлежит отрезку . Известно, что отрезок в два раза длиннее отрезка . Найти точку , если . Выполнить проверку.
б) Даны точки . Найти точку , делящую отрезок в отношении .
Читайте также:

