Частица в бесконечно глубокой потенциальной яме кратко

Обновлено: 07.07.2024

В квантовой физике частица, движущаяся в свободном пространстве, может обладать любой энергией. Ее энергетический спектр – сплошной . У частицы, которая движется в силовом поле, удерживающем ее в ограниченной области пространства, спектр собственных значений энергии оказывается дискретным . Примером может служить финитное (т. е. ограниченное) движение электрона в кулоновском поле ядра атома водорода. Дискретность энергетических уровней частиц, запертых в ограниченной области, вытекает из двойственной природы частиц и является принципиальным отличием квантовой физики от классической.

Таким образом, стационарным состояниям частицы, запертой в потенциальной яме, соответствует дискретный набор длин волн. Поскольку в квантово-механическом случае длина волны однозначно связана с импульсом частицы: , а импульс частицы определяет энергию ее движения: (нерелятивистское приближение), то квантованной оказывается и энергия частицы. Квантово-механический расчет приводит к следующему выражению:

Здесь – масса частицы, – постоянная Планка, – энергия наинизшего состояния.

Следует обратить внимание, что квантово-механическая частица в отличие от классической не может покоиться на дне потенциальной ямы, то есть иметь энергию . Это противоречило бы соотношению неопределенностей

Действительно, у покоящейся частицы импульс строго равен нулю, следовательно, . В то же время неопределенность координаты частицы . Поэтому произведение у частицы, лежащей на дне потенциальной ямы, должно было бы равняться нулю.

Соотношение неопределенностей позволяет сделать оценку минимальной энергии частицы. Если принять, что в состоянии с минимальной энергией , то для минимальной энергии получается выражения

Эта грубая оценка дает правильное по порядку величины значение .

Стоячие волны де Бройля, образующиеся при движении частицы в потенциальной яме, это и есть волновые или пси-функции, с помощью которых квантовая механика описывает стационарные состояния микрообъектов. Квадрат модуля волновой функции определяется как вероятность нахождения частицы в различных точках пространства.

В компьютерной модели можно изменять ширину потенциальной ямы, а также массу запертой в ней частицы. В левом окне высвечиваются графические изображения волновых функций или квадратов их модулей для нескольких стационарных состояний (). В правом окне изображается энергетический спектр частицы, то есть спектр возможных значений ее энергии. Обратите внимание, что энергетические уровни опускаются при увеличении ширины потенциальной ямы и массы запертой в ней частицы.

В компьютерной модели масса частицы выражается в массах протона _p = 1,67∙10 –27 кг. Следовательно, моделируются состояния сравнительно тяжелых частиц (ядер тяжелых атомов), оказавшихся в потенциальной яме с шириной порядка размеров атомов.

Рассмотрим поведение частицы в бесконечно глубокой одномерной прямоугольной потенциальной яме.

Предположим, что частица движется вдоль оси Движение частицы ограничено областью 0 ≤ ≤ , в которой потенциальная энергия частицы (потенциальная энергия отсчитывается от дна ямы). За пределами ямы при потенциальная энергия В пределах ямы частица движется свободно. Сталкиваясь со стенками ямы, она отражается от них и изменяет направление своего движения. За пределы потенциальной ямы частица выйти не может. Волновую функцию, зависящую только от одной координаты обозначим Тогда уравнение Шредингера (7.44.10) примет вид:

За пределы ямы частица выйти не может, поэтому вероятность обнаружить ее, а следовательно и волновая функция , за пределами ямы равна нулю. Из условия непрерывности следует, что и на границах ямы должна быть равна нулю, т.е.:

Этим граничным условиям должны удовлетворять решения уравнения (7.44.15). Обозначим Тогда уравнение (7.44.15) примет вид:

Решение уравнения (7.44.17) имеет вид:

Значения и найдем, используя граничные условия (7.44.16). Из условия получим:

откуда следует, что Выполнение условия

возможно в том случае, если

Из (7.44.19) следует, что решения уравнения будут иметь физический смысл лишь при значениях энергии, удовлетворяющих соотношению:

Отсюда найдем собственные значения энергии:

Условие квантования энергии получено непосредственно из решения уравнения Шредингера без дополнительных предположений. Подставив (7.44.20) в (7.44.18), получим собственные функции для данной задачи:

Коэффициент найдем из условия нормирования волновой функции:

С учетом (7.44.24) собственные функции принимают вид:

Графики функций изображены на рисунке для различных значений

Контрольные вопросы для самоподготовки студентов:

1.Что определяет квадрат модуля волновой функции?

2. Общее уравнение Шредингера.

3.Уравнение Шредингера для стационарных состояний.

Рассмотрим поведение частицы в бесконечно глубокой одномерной прямоугольной потенциальной яме.

Решение уравнения (7.44.17) имеет вид:

Значения и найдем, используя граничные условия (7.44.16). Из условия получим:

откуда следует, что Выполнение условия

возможно в том случае, если

Отсюда найдем собственные значения энергии:

Потенциальной ямой называют область пространства, в которой потенциальная энергия меньше, чем в соседних областях.

Пусть частица находится в одномерной бесконечно глубокой потенциальной яме.

В такой яме частица может двигаться вдоль оси х от точки х = 0 до точки х = L. В области х L частица проникнуть не может.

Классическая частица в такой ситуации может двигаться внутри ямы совершенно свободно, но за стенки ямы проникнуть не может. Ее скорость в яме может быть любой. В частности, энергия может равняться нулю, т.е. частица может просто покоиться в какой либо точке с координатой L > x > 0.

Если скорость классической частицы отлична от нуля, то частица должна совершать колебания между точками х = 0 и x = L – долетев до какой-либо стенки ямы, частица отразится от нее и полетит в противоположную сторону.

Поведение квантовой частицы, в отличие от классической, более сложно, хотя есть и некоторое сходство. Сходство заключается в том, что в такой ситуации квантовая частица тоже не может проникнуть за стенки потенциальной ямы (так как они бесконечно высоки). На языке квантовой механики это означает, что y(0) = 0, y(L) = 0.

Все остальные особенности поведения квантовой частицы можно найти, решив уравнение Шрёдингера для этой ситуации.

Поскольку яма бесконечно глубока, уравнение записываем лишь для области 0 i k 0 +Be -ik0 = A + B = 0,

y = A( ikx – e -ikx ).

Поскольку e ikx = coskx + isinkx, выражение для волновой функции можно привести к виду

y = 2iAsinkx = Csinkx.

Так как y(L) = 0,

CsinkL = 0.

Поскольку С ¹ 0, нулю должен равняться синус: sinkL = 0.

Отсюда следует, что kL=np, т.е. k не может принимать произвольные значения, ему разрешены лишь значения из ряда , где n = 1, 2, 3.

Это означает, что волновая функция может иметь лишь такой вид, при котором на ширине ямы укладывается целое число полуволн де Бройля: и .

Как известно, наложение встречных волн, отвечающих такому условию, вызывает возникновение стоячей волны.

Следовательно, в бесконечно глубокой потенциальной яме волновая функция может иметь такой вид, при котором на ширине ямы возникают стоячие волны де Бройля.

Таким образом, волновая функция, описывающая квантовую частицу в бесконечно глубокой прямоугольной потенциальной яме, имеет следующий вид:

По условию частица обязательнонаходится внутри потенциальной ямы. Это значит, что

Учитывая, что мы можем получить, что .

Поэтому функция y(x) принимает окончательный вид

Отметим еще одну важную особенность.

Поскольку и k может принимать лишь дискретные значения, полная энергия квантовой частицы также может принимать лишь некоторые значения, определяемые соотношением , где n = 1, 2, 3.

Квантовая частица в такой яме может существовать лишь в движении, причем в движении, отвечающем волновому числу и энергии .

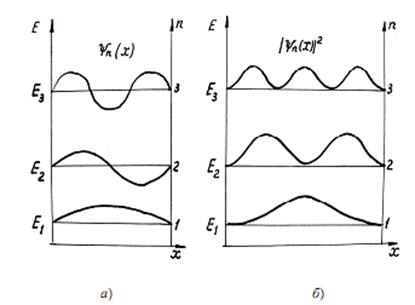
Вид волновых функций, соответствующих разрешенным состояниям, схематически изображен на рисунке.

Итак, квантовой частице в потенциальной яме разрешены лишь такие состояния, для которых на ширине ямы укладывается целое число полуволн де Бройля (т.е. разрешены состояния, для которых возможно возникновение стоячей волны де Бройля).

Как видно из рисунка, вероятность обнаружения частицы в разных точках ямы различна (у классической частицы она одинакова). Вероятность обнаружения частицы в той или иной точке зависит от координаты.

В состоянии с минимальной возможной энергией наиболее вероятно обнаружить частицу в центре ямы и практически невероятно обнаружить частицу у краев ямы.

Если частица имеет более высокую энергию (Е₂, Е₃ и т.д.), то вероятность обнаружения частицы в нескольких точках ямы максимальна. Между этими точками обязательно имеются такие, в которых квантовая частица не будет обнаружена никогда (точки, в которых квадрат модуля волновой функции равен нулю).

Квантовая частица может находиться на дискретных энергетических уровнях, разделенных интервалом .

Величина интервала зависит от массы частицы m, ширины потенциальной ямы L, значения квантового числа n.

Анализ выражения для расчета DE_n показывает, что интервал между соседними разрешенными значениями энергии квантовой частицы увеличивается по мере увеличения номера энергетического уровня n.

Чем больше масса квантовой частицы, тем ближе разрешенные уровни энергии частицы, тем ближе к непрерывному (классическому) спектр разрешенных значений энергии частицы.
И, наоборот, уменьшение массы частицы приводит к увеличению дискретности энергетических уровней. Другими словами, уменьшение массы частицы вызывает усиление проявления ее квантовых свойств.

С уменьшением ширины ямы дискретность энергетических уровней возрастает. Следовательно, чем точнее задается положение частицы, тем заметнее ее квантовый характер.

Следовательно, различия между квантовой и классической механикой становятся все менее заметными по мере увеличения массы частиц и ширины потенциальных ям, ограничивающих свободу перемещения частиц. Таким образом, квантовая механика ни в коей мере не перечеркивает классическую механику.

Частица в бесконечно глубокой одномерной потенциальной яме.
Прохождение частиц через потенциальный барьер

Частица в потенциальной яме. Чтобы пояснить сказанное в предыдущем параграфе, рассмотрим конкретный пример, достаточно простой для того, чтобы можно было решить уравнение Шредингера без большого труда.

Исследуем поведение частицы в бесконечно глубокой одномерной потенциальной яме. Предположим, что частица может двигаться только вдоль оси х. Пусть движение ограничено непроницаемыми для частицы стенками: х = 0 и х — I. Потенциальная энергия U имеет в этом случае следующий вид (рис. 195,а): она равна нулю при О i^x^Cl и обращается в бесконечность при х /.

(68.1)

За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружить частицу, а следовательно и функция -ф, за пределами ямы равна нулю. Далее, из условия непрерывности следует, что ф должна быть равна нулю и на границах ямы, т. е. что

Выражения (68.2) и определяют те условия, которым должны удовлетворять решения уравнения (68.1), имеющие физический смысл.

В области, где ф не равна тождественно нулю, уравнение (68.1) принимает следующий вид (U в этой области равна нулю):

Введя обозначение получим уравнение, хорошо известное из теории колебаний:

Решения такого уравнения, как известно 1 ), имеют вид;

Условиям (68.2) можно удовлетворить соответствующим выбором постоянных (о и а. Прежде всего, из условия яЬ(0) =0 получаем:

откуда следует, что а должна быть равна нулю. Далее, должно выполняться условие:

что возможно лишь в случае, если

(п = 0 отпадает, поскольку при этом получается *ф =0—■ частица нигде не находится).

Из (68.4) вытекает, что решения уравнения (68.3) будут иметь физический смысл не при всех значениях энергии £, а лишь при значениях, удовлетворяющих соотношению:

Таким образом, не прибегая ни к каким дополнительным предположениям (как это пришлось сделать Бору), мы получили квантование энергии частицы и нашли собственные значения этой энергии:

Схема энергетических уровней изображена на рис. 195,6, Произведем оценку расстояний между соседними уровнями для различных значений массы частицы т и ширины ямы /. Разность энергий двух соседних уровней равна

Если взять т гюрядка массы молекулы (~10~ 23 г), а/ порядка 10 см (молекулы газа в сосуде), получается

Столь густо расположенные энергетические уровни будут практически восприниматься как сплошной спектр энергии, так что хотя квантование энергии в принципе

будет иметь место, но на характере движения молекул сказываться не будет.

Аналогичный результат получается, если взять т порядка массы электрона (~10~ 27 г) при тех же размерах ямы (свободные электроны в металле). В этом случае

Однако совсем иной результат получается для электрона, если область, в пределах которой он движется, будет порядка атомных размеров (~10 -8 см). В этом случае

Очевидно, что в этом случае дискретность энергетических уровней будет проявляться весьма заметным образом.

Собственными функциями, как следует из условия (68.4), будут

Для нахождения коэффициента а воспользуемся условием нормировки (67.1), которое в данном случае запишется следующим образом:

На концах промежутка интегрирования подынтегральная функция обращается в нуль. Поэтому значение интеграла можно получить, умножив среднее значение s\n 2 (nnx/l) (равное, как известно, 1/2) на длину промежутка /.

В результате получится: а 2 (1/2)/— 1, откуда а — 1/2//. Таким образом, собственные функции имеют вид:

Графики функций (68.6) изображены на рис. 196, m На рис. 196,6 дана плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы, равная 1|уф*. Как следует из графиков, частица в состоянии*,

например, с п = 2 не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Такое поведение частицы,

очевидно, не совместимо с представлением о траекториях. Отметим, что согласно классическим представлениям все положения частицы в яме равновероятны.

Прохождение через барьер. Пусть частица, движущаяся слева направо, падает на потенциальный барьер

скорость частицы, но затем при х >/ снова принимает первоначальное значение). Если же Е меньше U₀ (как изображено на рисунке), то частица отражается от барьера и летит в обратную сторону; сквозь барьер частица проникнуть не может.

Совершенно иначе выглядит поведение частицы согласно квантовой механике. Во-первых, даже при £ > Uq имеется отличная от нуля вероятность того, что частица отразится от барьера и полетит в обратную сторону. Во-вторых, при Е /. Такое, совершенно невозможное с классической точки зрения, поведение микрочастицы вытекает непосредственно из уравнения Шредингера.

Рассмотрим случай Е

(68.7)

(68.8)

для областей I и III и

для области //, причем Е— U₀

Легко убедиться (хотя бы подстановкой), что общее решение уравнения Шредингера для каждой из трех областей имеет вид:

причем аир определяются из выражений:

Заметим, что решение вида e iax соответствует волне, распространяющейся в направлении оси х, а решение вида e~ iax — волне, распространяющейся в противоположном направлении. Чтобы это понять, вспомним, что обычная (звуковая, электромагнитная и т. п.) плоская волна, распространяющаяся в направлении оси х, имеет вид cos (tot — kx)_t а волна, распространяющаяся в на-

правлении убывания г, — вид cos (w/ + kx) [см. т. I, формулы (78.2) и .(78.5)]. В § 65 мы установили, что волновая функция свободной частицы, движущейся в направлении оси х, имеет вид (65.5). Если отбросить в этой формуле временной множитель, то для ф получится значение e l W ft > x . Для частицы, движущейся в противоположном направлении, нужно, очевидно, взять е-*№ к )*.

В области /// имеется только волна, лрошедшая через барьер и распространяющаяся слева направо. Поэтому коэффициент В₃ следует положить равным нулю. Для нахождения остальных коэффициентов воспользуемся условиями, которым должна удовлетворять функция ф. Для того чтобы i|) была непрерывна во всей области изменений х от —оо до'+оо, должны выполняться условия; ^i(O) =г|>₂(0) и л|>₂(0 =грз(/). Для того чтобы ф была гладкой, т. е. не имела изломов, должны выполняться условия: H>i(0) = i[)£(0) и ^(/^^(/J. Из этих условий вытекают соотношения:

Разделим все уравнения на А_х и введем обозначения:

Тогда уравнения (68.9) примут вид:

Отношение каадратов модулей амплитуд отраженной и падающей волны

определяет вероятность отражения частицы от потенциального барьера и может быть названо коэффициентом отражения.

Отношение квадратов модулей прошедшей и падающей волны

определяет вероятность прохождения частицы через барьер и может быть названо коэффициентом прохождения (или коэффициентом прозрачности).

Нас будет интересовать только прохождение частиц через барьер, и мы ограничимся нахождением величины D. Правда, найдя D, легко найти R, поскольку эти коэффициенты связаны очевидным соотношением: /? + £> = 1.

Умножим первое из уравнений (68.11) на I и сложим с третьим. В результате получим:

Теперь умножим второе из уравнений (68.11) на i и вычтем его из четвертого. Получим:

Решая совместно уравнения (68.13) и (68.14), найдем, что

Наконец, подставив найденные нами значения а₂ и Ь₂ во второе из уравнений (68.11), получим выражение для аз*.

обычно бывает много больше единицы. Поэтому в знаменателе выражения для а$ слагаемым, содержащим мно-

житель, можно пренебречь по сравнению со слагаемым, содержащим множитель (комплексные числа п + i и п — i имеют одинаковый модуль). Итак, можно положить

Согласно (68.12) квадрат модуля этой величины дает вероятность прохождения частицы через потенциальный

барьер. Учтя, что, получим:

Как следует из полученного нами выражения, вероятность прохождения частицы через потенциальный барьер сильно зависит от ширины барьера / и от его превышения над Е, т. е. от U₀ — Е. Если при какой-то ширине барьера коэффициент прохождения D равен, допустим, 0,01, то при увеличении ширины в два раза D станет равным 0,01 2 = 0,0001, т.е. уменьшается в 100 раз. Тот же эффект в этом случае вызвало бы возрастание в четыре раза величины U₀ — Е. Коэффициент прохождения резко уменьшается при увеличении массы частицы т.

В случае потенциального барьера произвольной формы (см., например, рис. 197,6) формула (68.15) должна быть заменена более общей формулой:

[см. формулу (68.8)1.

Выражение имеет величину порядки

единицы 1 ). Поэтому можно считать, что

Введем волновой вектор , обозначив

и перепишем уравнение в виде

Существуют, как известно, два линейно независимых решения уравнения (4.22), так что общее решение есть суперпозиция двух волн — или стоячих:

или бегущих:

(первый член — волна бежит направо, второй — налево; постоянные и произвольны). Аналогия: такие же решения описывают колебания свободной струны. Поскольку возможны волны с произвольным значением волнового числа , энергия частицы () также может принимать любые значения, то есть, в данном случае свободного инфинитного движения — не квантуется. Для частицы, движущейся в произвольном направлении вдоль произвольно направленного волнового вектора , справедливы те же решения при замене

При решении большинства задач квантовой механики следует обратить внимание на то, что волновая функция всегда должна быть непрерывной — вероятность пребывания частицы не может меняться скачком от точки к точке. Кроме того, если потенциальная энергия непрерывна или имеет скачки, но только первого рода (конечные скачки) и не имеет бесконечных скачков (скачков второго рода), то из уравнения Шредингера следует, что и первая производная волновой функции также непрерывна.

Частица в бесконечно глубокой потенциальной яме

Потенциальная энергия в этой задаче имеет вид

Такая система соответствует частице, движущейся вдоль прямой линии и отскакивающей от абсолютно отражающих препятствий в точках и . В область бесконечного потенциала частица проникнуть не может, следовательно, за пределами отрезка . Внутри ямы , и стационарное уравнение Шредингера имеет тот же вид, как для свободной частицы. Получатся те же решения в виде суперпозиции стоячих (или бегущих) волн, но в отличие от предыдущего случая добавятся граничные условия. Именно, в точках и волновая функция должна обращаться в нуль (поскольку она непрерывна и равна нулю вне ямы). В классической механике точно такие граничные условия имеет уравнение для струны с закрепленными концами.

Общее решение имеет вид

Используем сначала первое граничное условие

Мы получили, что решение уравнения Шредингера должно иметь вид

Если продолжить нашу аналогию, то можно сказать, что на струне, закрепленной в одной точке, бегущих волн не бывает: отражение от неподвижной точки обязательно порождает стоячую волну. Однако на длину волны никаких ограничений не накладывается.

Теперь наложим второе из граничных условий:

Здесь есть два типа решений. При получаем

что означает отсутствие частицы в яме (вероятность найти ее всюду равна нулю). Поэтому нас интересует второе – нетривиальное – решение, когда

Это возможно лишь при некоторых значениях волнового вектора:

Так как энергия частицы связана с волновым вектором, то

Подставляя найденные разрешенные значения волнового вектора в выражение для волновой функции, получаем ее в виде

Смысл квантового числа: оно на единицу больше числа нулей волновой функции. Значение постоянной

определяется из условия нормировки.

Рис. 4.8. Уровни энергии, волновые функции и распределение плотности вероятностей по координате x

Отметим, что значения , при которых граничное условие в точке также будет выполнено, новых состояний не дают. Это видно и из выражения для энергии (4.24), в которое n входит в квадрате, и из выражения для волновой функции (4.25): изменение знака n приведет лишь к изменению знака волновой функции , что оставит неизменным распределение вероятностей .

Откуда же берется дискретность уровней энергии, характерная и для атома? Сравним со свободной частицей: уравнения те же, но с иными граничными условиями! Здесь возможны две постановки задачи. В первом случае исследуется состояние, которому в классической механике соответствовало бы инфинитное движение (задача рассеяния). Обычно в таких случаях решения возможны при любых значениях энергии (как говорят, спектр непрерывен). Во втором случае исследуется состояние, которому в классике соответствует финитное движение в ограниченной области пространства (задача на связанные состояния). Требование конечности волновой функции во всем пространстве ведет к квантованию энергии. Подчеркнем: в этом случае стационарное уравнение имеет физически приемлемые решения не всегда, а лишь при некоторых значениях энергии . Как следствие возникает дискретный спектр энергии системы.

Пример. Определим разность соседних уровней энергии для частицы в бесконечно глубокой потенциальной яме при больших значениях n. Полученный результат используем для оценки разности энергий соседних уровней энергии поступательного движения молекул азота при комнатной температуре в сосуде. Примем массу молекулы , а линейный размер сосуда . Сравним полученный результат с кинетической энергией поступательного движения молекул азота.

Используя выражение (4.24) для уровней энергии частицы в потенциальной яме, находим разность энергий соседних уровней

при больших значениях . Средняя кинетическая энергия поступательного движения молекул азота равна

Приравнивая выражению (4.24) для энергии уровней частицы в яме, находим, что такая энергия соответствует квантовым числам порядка

Уже само по себе это число говорит о том, что в области крайне высоких возбуждений работают классические формулы. Разность энергий соседних уровней получается, подстановкой в формулу для найденного выражения для квантового числа:

В электрон-вольтах те же характеристики имеют значения

Относительная разность энергий соседних уровней ничтожно мала:

и потому в классическом пределе квантовой дискретностью пренебрегают.

Частица в трехмерной потенциальной яме

Это обобщение предыдущей задачи. Частица может двигаться в кубическом объеме с длиной ребра . Нетрудно убедиться, что общее решение для волновой функции представимо в виде произведения одномерных волновых функций, полученных в предыдущей задаче:

Такая волновая функция соответствует очевидному факту, что движения вдоль трех осей не зависят друг от друга, и каждое описывается прежними одномерными волновыми функциями. Энергия, как легко догадаться, будет равна сумме энергий движения по осям x, y, z:

Рис. 4.9. Трёхмерная потенциальная яма

Состояние системы теперь определяется тремя квантовыми числами ₁, ₂ и ₃, принимающими, как и прежде; целые значения. Здесь мы впервые сталкиваемся с важным понятием вырождения энергетических уровней, то есть с ситуацией, когда разные состояния системы имеют одинаковую энергию. В самом деле, минимальная энергия системы достигается при минимальных значениях всех квантовых чисел, то есть при ₁, ₂, ₃. Эта энергия равна

и ей соответствует одна волновая функция . Говорят, что основное состояние не вырождено (невырожденность состояния с минимальной энергией — общее правило). Первое возбужденное состояние получается, когда одно из квантовых чисел равно 2, а остальные по-прежнему равны единице; энергия его

Но такую энергию имеют теперь три состояния с волновыми функциями , , и (квантовое число 2 можно выбрать тремя способами), поэтому говорят, что кратность вырождения первого возбужденного уровня равна трем (g = 3). Естественно, в другой системе может быть совершенно иная кратность вырождения (или отсутствие такового). Последующие состояния частицы в трехмерной потенциальной яме с бесконечными стенками также вырождены. Ясно, что вырождение уровней связано с симметрией системы, с равноправием всех осей. Если бы размеры ямы были разными ₁, ₂, ₃ то всем трем направлениям, то для энергии мы бы получили вместо (4.27) выражение

и вырождение могло бы иметь место лишь при определенных соотношениях между длиной, шириной и высотой потенциального ящика.

Одномерный осциллятор

В классической физике пружинный маятник (одномерный осциллятор) представляет собой точечное тело массой m, прикрепленное к пружине и колеблющееся с круговой частотой . Потенциальная энергия такой системы описывается выражением

так что уравнение Шредингера записывается в виде

Отсюда можно найти решение для волновой функции основного состояния

Подставляя это выражение в уравнение Шредингера, легко убедиться, что энергия основного состояния равна

Мы не выписываем волновые функции возбужденных состояний осциллятора, но выражение для разрешенных значений энергии имеет вид ( — колебательное квантовое число)

Здесь воспроизводится формула Планка и нулевые колебания

полученные ранее из соотношения неопределенностей (см. разд. 3.3).

Рис. 4.10. Уровни энергии и распределения плотности вероятностей по координате x для разных значений колебательного квантового числа. График потенциальной энергии осциллятора показан синей линией

Рис. 4.11. Распределения вероятностей для классического (пунктир) и квантового (сплошная линия) осцилляторов.
a) n = 1; б) большие значения n

Трехмерный осциллятор

Эта задача является обобщением предыдущей. Как и для трехмерной потенциальной ямы с бесконечно высокими стенками, волновая функция представляется в виде произведения волновых функций одномерных осцилляторов, колеблющихся независимо вдоль осей ,,. Так, волновая функция основного состояния имеет вид

а уровни энергии трехмерного осциллятора описываются формулой

В отличие от одномерного осциллятора состояние определяется значениями трех квантовых чисел ₁, ₂, ₃. Легко понять, что все возбужденные состояния должны быть вырожденными.

Читайте также: