Биноминальное распределение это кратко

Обновлено: 05.07.2024

В настоящей и нескольких следующих заметках мы рассмотрим математические модели случайных событий. Математическая модель — это математическое выражение, представляющее случайную величину. Для дискретных случайных величин это математическое выражение известно под названием функция распределения. [1]

Если задача позволяет явно записать математическое выражение, представляющее случайную величину, можно вычислить точную вероятность любого ее значения. В этом случае можно вычислить и перечислить все значения функции распределения. В деловых, социологических и медицинских приложениях встречаются разнообразные распределения случайных величин. Одним из наиболее полезных распределений является биномиальное.

Биномиальное распределение используется для моделирования ситуаций, характеризующихся следующими особенностями.

Выборка состоит из фиксированного числа элементов n, представляющих собой исходы некоего испытания.
Каждый элемент выборки принадлежит одной из двух взаимоисключающих категорий, исчерпывающих все выборочное пространство. Как правило, эти две категории называют успех и неудача.
Вероятность успеха р является постоянной. Следовательно, вероятность неудачи равна 1 – р.
Исход (т.е. удача или неудача) любого испытания не зависит от результата другого испытания. Чтобы гарантировать независимость исходов, элементы выборки, как правило, получают с помощью двух разных методов. Каждый элемент выборки случайным образом извлекается из бесконечной генеральной совокупности без возвращения или из конечной генеральной совокупности с возвращением.

Биномиальное распределение используется для оценки количества успехов в выборке, состоящей из n наблюдений. Рассмотрим в качестве примера оформление заказов. Чтобы сделать заказ клиенты компании Saxon Company могут воспользоваться интерактивной электронной формой и послать ее в компанию. Затем информационная система проверяет, нет ли в заказах ошибок, а также неполной или недостоверной информации. Любой заказ, вызывающий сомнения, помечается и включается в ежедневный отчет об исключительных ситуациях. Данные, собранные компанией, свидетельствуют, что вероятность ошибок в заказах равна 0,1. Компания хотела бы знать, какова вероятность обнаружить определенное количество ошибочных заказов в заданной выборке. Например, предположим, что клиенты заполнили четыре электронных формы. Какова вероятность, что все заказы окажутся безошибочными? Как вычислить эту вероятность? Под успехом будем понимать ошибку при заполнении формы, а все остальные исходы будем считать неудачей. Напомним, что нас интересует количество ошибочных заказов в заданной выборке.

Какие исходы мы можем наблюдать? Если выборка состоит из четырех заказов, ошибочными могут оказаться один, два, три или все четыре, кроме того, все они могут оказаться правильно заполненными. Может ли случайная величина, описывающая количество неправильно заполненных форм, принимать какое-либо иное значение? Это невозможно, поскольку количество неправильно заполненных форм не может превышать объем выборки n или быть отрицательным. Таким образом, случайная величина, подчиняющаяся биномиальному закону распределения, принимает значения от 0 до n.

Допустим, что в выборке из четырех заказов наблюдаются следующие исходы:

Какова вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, причем в указанной последовательности? Поскольку предварительные исследования показали, что вероятность ошибки при заполнении формы равна 0,10, вероятности указанных выше исходов вычисляются следующим образом:

Поскольку исходы не зависят друг от друга, вероятность указанной последовательности исходов равна: р*р*(1–р)*р = 0,1*0,1*0,9*0,1 = 0,0009. Если же необходимо вычислить количество вариантов выбора X объектов из выборки, содержащей n элементов, следует воспользоваться формулой сочетаний (1):

где n! = n * (n –1) * (n – 2) * … * 2 * 1 — факториал числа n, причем 0! = 1 и 1! = 1 по определению.

Это выражение часто обозначают как . Таким образом, если n = 4 и X = 3, количество последовательностей, состоящих из трех элементов, извлеченных из выборки, объем которой равен 4, определяется по следующей формуле:

Следовательно, вероятность обнаружить три ошибочных заказа вычисляется следующим образом:

(Количество возможных последовательностей) *
(вероятность конкретной последовательности) = 4 * 0,0009 = 0,0036

Аналогично можно вычислить вероятность того, что среди четырех заказов окажутся один или два ошибочных, а также вероятность того, что все заказы ошибочны или все верны. Однако при увеличении объема выборки n определить вероятность конкретной последовательности исходов становится труднее. В этом случае следует применить соответствующую математическую модель, описывающую биномиальное распределение количества вариантов выбора X объектов из выборки, содержащей n элементов.

где Р(Х) — вероятность X успехов при заданных объеме выборки n и вероятности успеха р, X = 0, 1, … n.

Обратите внимание на то, что формула (2) представляет собой формализацию интуитивных выводов. Случайная величина X, подчиняющаяся биномиальному распределению, может принимать любое целое значение в диапазоне от 0 до n. Произведение р X (1 – р) n – X представляет собой вероятность конкретной последовательности, состоящей из X успехов в выборке, объем которой равен n. Величина определяет количество возможных комбинаций, состоящих из X успехов в n испытаниях. Следовательно, при заданном количестве испытаний n и вероятности успеха р вероятность последовательности, состоящей из X успехов, равна

Р(Х) = (количество возможных последовательностей) * (вероятность конкретной последовательности) =

Рассмотрим примеры, иллюстрирующие применение формулы (2).

1. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм три окажутся ошибочными? Используя формулу (2), получаем, что вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, равна

2. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными? Как показано в предыдущем примере, вероятность того, что среди четырех заполненных форм три окажутся ошибочными, равна 0,0036. Чтобы вычислить вероятность того, что среди четырех заполненных форм не менее трех будут неправильно заполнены, необходимо сложить вероятность того, что среди четырех заполненных форм три окажутся ошибочными, и вероятность того, что среди четырех заполненных форм все окажутся ошибочными. Вероятность второго события равна

Таким образом, вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными, равна

Р(Х > 3) = Р(Х = 3) + Р(Х = 4) = 0,0036 + 0,0001 = 0,0037

3. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм менее трех окажутся ошибочными? Вероятность этого события

Р(X 3. Тогда Р(Х 3) = 1 – 0,0037 = 0,9963.

По мере увеличения объема выборки n вычисления, аналогичные проведенным в примере 3, становятся затруднительными. Чтобы избегать этих сложностей, многие биномиальные вероятности табулируют заранее. Некоторые из этих вероятностей приведены рис. 1. Например, чтобы получить вероятность, что Х = 2 при n = 4 и p = 0,1, следует извлечь из таблицы число, стоящее на пересечении строки Х = 2 и столбца р = 0,1.

Рис. 1. Биномиальная вероятность при n = 4, Х = 2 и р = 0,1

Биномиальное распределение можно вычислить с помощью функции Excel =БИНОМ.РАСП() (рис. 2), имеющей 4 параметра: число успехов – Х, число испытаний (или объем выборки) – n, вероятность успеха – р, параметр интегральная, принимающий значения ИСТИНА (в этом случае вычисляется вероятность не менее Х событий) или ЛОЖЬ (в этом случае вычисляется вероятность точно Х событий).

Рис. 2. Параметры функции =БИНОМ.РАСП()

Для вышеприведенных трех примеров расчеты приведены на рис. 3 (см. также Excel-файл). В каждом столбце приведено по одной формуле. Цифрами показаны ответы на примеры соответствующего номера).

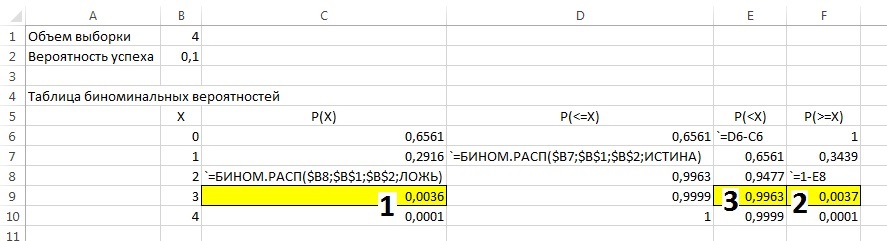
Рис. 3. Расчет биноминального распределения в Excel для n = 4 и p = 0,1

Свойства биномиального распределения

Биномиальное распределение зависит от параметров n и р. Биномиальное распределение может быть, как симметричным, так и асимметричным. Если р = 0,5, биномиальное распределение является симметричным независимо от величины параметра n. Однако, если р ≠ 0,5, распределение становится асимметричным. Чем ближе значение параметра р к 0,5 и чем больше объем выборки n, тем слабее выражена асимметрия распределения. Таким образом, распределение количества неправильно заполненных форм смещено вправо, поскольку p = 0,1 (рис. 4).

Рис. 4. Гистограмма биномиального распределения при n = 4 и p = 0,1

Математическое ожидание биномиального распределения равно произведению объема выборки n на вероятность успеха р:

В среднем, при достаточно долгой серии испытаний в выборке, состоящей из четырех заказов, может оказаться р = Е(Х) = 4 х 0,1 = 0,4 неправильно заполненных форм.

Стандартное отклонение биномиального распределения

Например, стандартное отклонение количества неверно заполненных форм в бухгалтерской информационной системе равно:

[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 307–313

Или биномиальный закон распределения вероятностей. Исходя из моих наблюдений и личной статистики – это наиболее распространённый вид дискретного распределения, с которым мы уже встречались добрый десяток раз.

Я буду формулировать задачу в общем виде и попутно приводить конкретный пример:

Пусть проводится независимых испытаний (не обязательно повторных), в каждом из которых случайное событие может появиться с вероятностью. Тогда случайная величина – число появлений события в данной серии испытаний, имеет биномиальное распределение.

Совершенно понятно, что эта случайная величина может принять одно из следующих значений: .

Например: монета подбрасывается 5 раз. Тогда случайная величина – количество появлений орла распределена по биномиальному закону. Орёл обязательно выпадет:

или раз, или , или , или , или , или раз.

Как вы догадались, соответствующие вероятности определяются формулой Бернулли:

– количество независимых испытаний;
– вероятность появления события в каждом испытании;
– вероятность непоявления события в каждом испытании;
– сколько раз может появиться событие в данной серии испытаний (список всех возможных значений).

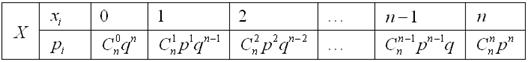
Сведём этот закон распределения в таблицу:

Вероятности представляют собой члены бинома Ньютона, благодаря чему распределение и получило своё название. По формуле бинома:
, что мы и ожидали увидеть.

В нашем примере с монеткой:

– вероятность того, что в 5 испытаниях орёл не выпадет вообще ();

– вероятность того, что в 5 испытаниях орёл выпадет ровно раз;

– вероятность того, что в 5 испытаниях орёл выпадет ровно раза;

Таким образом, закон распределения числа выпавших орлов:

Поэтому вычисления целесообразно автоматизировать в Экселе с помощью его стандартной функции:

=БИНОМРАСП(m; n; p; 0), где количество успехов в испытаниях, а – вероятность успеха в каждом испытании.

Именно так реализован Пункт 3 моего расчётного макета по ТерВеру, ну и особо крутая плюшка – это Пункт 6, в котором биномиальное распределение получается автоматически!

Однако на практике решение нужно расписывать подробно, да и техника не всегда бывает под рукой. В этой связи обязательно прорешайте хотя бы 2-3 типовых задачи и постукайте пальцами по клавишам микрокалькулятора.

Вероятность поражения цели при одном выстреле равна 0,6. Составить закон распределения случайной величины – числа попаданий в цель при четырех выстрелах. Вычислить и . Построить многоугольник и функцию распределения. Найти .

…таких задач очень много – составить закон распределения вероятностей и найти всё-всё-всё. Или почти всё. Или что-то ещё – зависит от фантазии составителя :)

Решение: по существу, текст условия совпадает с Задачей статьи о геометрическом распределении, но есть одно принципиальное отличие – здесь другая случайная величина. А именно, ~~под страхом расстрела~~ совершается серия из и строго из 4 выстрелов, вероятность попадания в каждом из которых составляет .

Очевидно, что испытания независимы, и случайная величина распределена по биномиальному закону.

Составим ряд распределения данной случайной величины. Используем формулу Бернулли:
для – всех возможных результатов рассматриваемой серии.

На этом шаге я сразу забью в свой расчётный макет (Пункт 6), чтобы контролировать правильность каждого пункта. Для удобства их можно нумеровать:

0)
– вероятность того, что в 4 выстрелах не будет попаданий;

1)
– вероятность того, что в 4 выстрелах будет ровно 1 попадание;

2)
– … ровно 2 попадания;

3)
– … ровно 3 попадания;

4)
– … ровно 4 попадания.

Таким образом, искомый закон распределения:

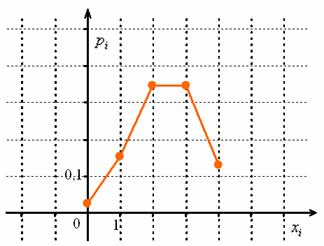
Пока таблица не ушла из поля зрения, построим многоугольник распределения:

Вычислим математическое ожидание и дисперсию. И тут есть отличная новость – для биномиального распределения можно не использовать общий алгоритм расчёта этих числовых характеристик – по той причине, что существуют готовые формулы:

– среднеожидаемое количество попаданий;

– рассеяние количества попаданий относительно матожидания.

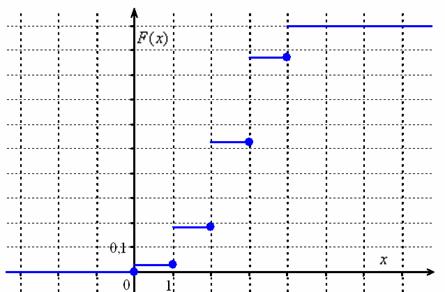
Я не буду вновь останавливаться на алгоритме её построения, и если что-то не понятно, то смотрите по ссылке выше. Раз ступенька, два ступенька – будет график:

Напоминаю, что в статье о функции распределения можно разыскать программу, которая строит чертежи автоматически.

Найдём – вероятность того, что значение случайной величины отклонится от своего математического ожидания не более чем на одно среднее квадратическое отклонение.

Среднее квадратическое отклонение:

и искомая вероятность:

(в чём смысл этого пункта решения?)

Дополнительные и многочисленные задания по теме можно найти в pdf-сборнике, и как я рекомендовал выше – непременно прорешайте пару-тройку задач вручную! Как говорится, автопилот хорошо, но без ручного управления – финиш.

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Рассмотрим осуществление схемы Бернулли, т.е. прозводится серия повторных независимых испытаний, в каждом из которых данное событие А имеет одну и ту же вероятность , не зависящую от номера испытания. И для каждого испытания имеются только два исхода:

1) событие А – успех;

2) событие - неуспех,

с постоянными вероятностями

Вероятность того, что случайную величину Х примет значение x_k находится по формуле Бернулли

(1)

Закон распределения дискретной случайной величины, определяемый формулой Бернулли (1), называется биномиальным законом распределения. Постоянные п и р (q=1-p), входящие в формулу (1) называются параметрами биномиального распределения.

(2)

А так как p+q=1, то правая часть равенства (2) равна 1

(3)

Это означает, что

(4)

В равенстве (3) первый член q n в правой части означает вероятность того, что в п испытаниях событие А не появится ни разу, второй член вероятность того, что событие А появится один раз, третий член – вероятность, что событие А появится два раза и наконец, последний член р п – вероятность того, что событие А появится ровно п раз.

Биномиальный закон распределения дискретной случайной величины представляют в виде таблицы:

Х	0	1	…	k	…	n
Р	q n		…		…	р п

Основные числовые характеристики биномиального распределения:

1) математическое ожидание (5)

2) дисперсия (6)

3) среднее квадратическое отклонение (7)

4) наивероятнейшее число появление события k₀ – это число которому при заданном п соответствует максимальная биномиальная вероятность

При заданных п и р это число определяется неравенствами

(8)

если число пр+р не является целым, то k₀ равно целой части этого числа, если же пр+р – целое число, то k₀ имеет два значения

Биномиальный закон распределения вероятностей применяется в теории стрельбы, в теории и практике статистического контроля качества продукции, в теории массового обслуживания, в теории надежности и т.д. Этот закон может применяться во всех случаях, когда имеет место последовательность независимых испытаний.

Пример 1: Проверкой качества установлено, что из каждых 100 приборов не имеют дефекты 90 штук в среднем. Составить биномиальный закон распределения вероятностей числа качественных приборов из приобретенных наугад 4.

Случайная величина Х – число качественных приборов из взятых 4, значит значения Х -Найдем вероятности значений Х по формуле (1):

Таким образом, закон распределения величины Х - число качественных приборов из взятых 4:

Х	0	1	2	3	4
Р	0,0001	0,0036	0,0486	0,2916	0,6561

Для проверки правильности построения распределения проверим чему равна сумма вероятностей

Ответ: Закон распределения

Х	0	1	2	3	4
Р	0,0001	0,0036	0,0486	0,2916	0,6561

Пример 2: Применяемый метод лечения приводит к выздоровлению в 95 % случаев. Пятеро больных применяли данный метод. Найти наивероятнейшее число выздоровевших, а так же числовые характеристики случайной величины Х – число выздоровевших из 5 больных применявших данный метод.

Решение: Событие А - больной применявший лечение выздоровел, тогда основные параметры биномиального распределения:

По формуле (8) найдем наивероятнейшее число выздоровевших из 5. Найдем получили не целое число значитравно целой части, т.е. .

Теперь найдем числовые характеристики Х – число выздоровевших из 5 больных применявших данный метод лечения:

1) математическое ожидание по формуле (5)

2) дисперсия по формуле (6)

3) среднее квадратическое отклонение по формуле (7)

Ответ:

1) событие А – успех;

2) событие - неуспех,

с постоянными вероятностями

Вероятность того, что случайную величину Х примет значение x_k находится по формуле Бернулли

(1)

(2)

А так как p+q=1, то правая часть равенства (2) равна 1

(3)

Это означает, что

(4)

Биномиальный закон распределения дискретной случайной величины представляют в виде таблицы:

Х	0	1	…	k	…	n
Р	q n		…		…	р п

Основные числовые характеристики биномиального распределения:

1) математическое ожидание (5)

2) дисперсия (6)

3) среднее квадратическое отклонение (7)

При заданных п и р это число определяется неравенствами

(8)

Таким образом, закон распределения величины Х - число качественных приборов из взятых 4:

Х	0	1	2	3	4
Р	0,0001	0,0036	0,0486	0,2916	0,6561

Для проверки правильности построения распределения проверим чему равна сумма вероятностей

Ответ: Закон распределения

Х	0	1	2	3	4
Р	0,0001	0,0036	0,0486	0,2916	0,6561

1) математическое ожидание по формуле (5)

2) дисперсия по формуле (6)

3) среднее квадратическое отклонение по формуле (7)

Содержание

Определение

$X_1 ,\ldots, X_n$

Пусть — конечная последовательность независимых случайных величин с распределением Бернулли, то есть

$X_i = \left\< \begin 1, & p \\ 0, & q \equiv 1-p \end \right.,\; i=1,\ldots, n.$

$Y\!$

Построим случайную величину :

$Y = \sum\limits_<i=1> ^n X_i$
.

$p_Y(k) \equiv \mathbb (Y = k) = \binom\, p^k q^,\; k=0,\ldots, n,$

$\binom<n> где = \frac$
— биномиальный коэффициент.

Функция распределения

Функция распределения биномиального распределения может быть записана в виде суммы:

$F_Y(y) \equiv \mathbb (Y \leqslant y) = \sum\limits_^ <\lfloor y \rfloor>\binom\, p^k q^,\; y \in\mathbb$
,

где обозначает наибольшее целое, не превосходящее число , или в виде неполной бета-функции:

$F_Y(y) \equiv \mathbb (Y \leqslant y ) = I_(n-\lfloor y \rfloor,\lfloor y \rfloor +1)$
.

Моменты

Производящая функция моментов биномиального распределения имеет вид:

$M_Y(t) = \left( pe^t + q\right)^n$

[Y] = np" width="" height="" />
, \left[Y^2\right] = np ( q + np )" width="" height="" />
,

а дисперсия случайной величины.

$\mathbb<D> [Y] = npq$
.

Свойства биномиального распределения

Связь с другими распределениями

См. также

Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.
Эта отметка установлена 12 мая 2011.

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое "Биномиальное распределение" в других словарях:

БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ — (binomial distribution) Распределение, позволяющее рассчитать вероятность наступления какого либо случайного события, полученного в результате наблюдений ряда независимых событий, если вероятность наступления, составляющих его элементарных… … Экономический словарь

БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ — (распределение Бернулли) распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна p(0 p 1). Именно, число ? появлений этого события есть… … Большой Энциклопедический словарь

биномиальное распределение — (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна р (0≤р≤1). Именно, число μ появлений этого события… … Энциклопедический словарь

биномиальное распределение — 1.49. биномиальное распределение Распределение вероятностей дискретной случайной величины X, принимающей любые целые значения от 0 до n, такое что при х = 0, 1, 2, . n и параметрах n = 1, 2, . и 0 Словарь-справочник терминов нормативно-технической документации

БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ — распределение Бернулли, распределение вероятностей случайной величины X, принимающей целочисленные значения с вероятностями соответственно ( биномиальный коэффициент; р параметр Б. р., наз. вероятностью положительного исхода, принимающей значения … Математическая энциклопедия

Биномиальное распределение — распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях. Если при каждом испытании вероятность появления события равна р, причём 0 ≤ p ≤ 1, то число μ появлений этого события при n независимых… … Большая советская энциклопедия

БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ — (распределение Бернулли), распределение вероятностей числа появлений нек рого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна р (0 Естествознание. Энциклопедический словарь

Биномиальное распределение вероятностей — (binomial distribution) Распределение, которое наблюдается в случаях, когда исход каждого независимого эксперимента (статистического наблюдения) принимает одно из двух возможных значений: победа или поражение, включение или исключение, плюс или … Экономико-математический словарь

биномиальное распределение вероятностей — Распределение, которое наблюдается в случаях, когда исход каждого независимого эксперимента (статистического наблюдения) принимает одно из двух возможных значений: победа или поражение, включение или исключение, плюс или минус, 0 или 1. То есть… … Справочник технического переводчика

Читайте также: