Алгоритм дейкстры кратко и понятно

Обновлено: 04.07.2024

Алгоритм Дейкстры – это последовательность действий, позволяющих оптимально найти на графе кратчайший путь от некоторой его вершины до всех остальных.

Граф представляет собой набор точек, называемых вершинами графа, и соединяющих их линий, называемых рёбрами.

Кратчайший путь между вершинами – это путь минимально возможной длины, соединяющий на графе одну вершину с другой.

Длина пути – это сумма длин всех дуг (ориентированных рёбер – рёбер с чётко указанными началом и концом), по которым проходит этот путь.

Длины дуг, называемые ещё весовыми коэффициентами, предполагаются известными. Если в графе нет дуги, соединяющей некоторые две отдельные вершины, то её длина условно считается равной бесконечности.

Алгоритм Дейкстры применяется исключительно для графов с неотрицательными длинами дуг.

Понятно, что для любых двух вершин произвольного графа могут существовать сразу несколько путей, соединяющих их. Чтобы найти кратчайший из этих путей будем придерживаться специальной стратегии, действуя согласно алгоритму, разработанному нидерландским учёным Дейкстрой.

Основная идея данного алгоритма заключается в том, что на каждом шаге помечается определённым образом выбранная вершина, а далее просматриваются все последующие (ещё не отмеченные) вершины графа и вычисляется длина пути до каждой из них от начальной точки.

Помеченная на каждом этапе новая вершина (та, до которой путь оказался кратчайшим) становится определяющей для следующего шага. И этот построенный до неё кратчайший путь закрашивается.

Повторяя данные действия, последовательно просматривая и поочерёдно отмечая вершины графа, в итоге добираемся до конечного пункта. Те рёбра графа, которые в результате оказались закрашенными (вместе с отмеченными их крайними точками), образуют ориентированное дерево кратчайших путей (с корнем в исходной вершине графа). Далее остаётся выбрать на нём путь, который соединяет начальную точку с конечной. Это и будет искомый путь.

Готовые работы на аналогичную тему

Пример поиска кратчайшего пути по алгоритму

Рассмотрим применение алгоритма Дейкстры к конкретному примеру. Пусть задан граф, представленный на рисунке:

Рисунок 1. Граф. Автор24 — интернет-биржа студенческих работ

Перед началом выполнения алгоритма все вершины и дуги на графе не раскрашены. Нужно найти и закрасить кратчайший путь от вершины $s$ до вершины $t$.

Для этого на каждом шаге по определённым правилам строятся пути, ведущие от начальной вершины $s$ до всех неотмеченных на графе вершин (обозначаемых здесь $y$), и далее из этих маршрутов выбирается условно кратчайший путь.

При переходе к каждой следующей итерации алгоритма среди всех непомеченных точек на графе отмечается та вершина (обозначается буквой $x$), до которой путь из вершины $s$ оказался самым коротким на этом шаге.

Каждый раз длина пути пересчитывается по формуле:

$r(x,y)$ – вес дуги, соединяющей вершины $x$ и $y$,
$S(y)$ – длина пути, соединяющего начальную точку $s$ с вершиной $y$.

Применим теперь данный алгоритм к графу, изображённому на рисунке.

Поскольку, очевидно, $S(s) = 0$ – самое короткое расстояние на графе (от стартовой точки $s$ до неё же), то отмечаем вершину $s$. При этом изначально считается, что $S(y) = ∞$ для всех остальных (отличных от $s$) вершин заданного графа.

Согласно алгоритму полагаем, что $x = s$. И далее вычисляем величины $S(y)$ для всех непомеченных вершин графа:

Выбираем среди полученных величин минимальную. В данном случае это $S(c) = 2$. Поэтому отмечаем вершину $c$ и закрашиваем дугу $(s,c)$, которая соответствует кратчайшему пути с длиной $S(c)$.

Продолжаем далее, пока не пройдём по графу до конечного пункта – вершины $t$. Сейчас оказалось, что $x = c$. И теперь по формуле пересчитываем величины $S(y)$ для ещё не отмеченных вершин:

Так как величина $S(a) = 5$ является минимальной из всех полученных на этом шаге величин, то отмечаем вершину $a$ и закрашиваем на графе дугу $(s,a)$, которая и определяет величину $S(a)$.

Аналогично предыдущему шагу за точку $x$ принимаем только что помеченную точку: $x = a$. Снова пересчитываем величины $S(y)$ для оставшихся вершин:

Поскольку величина $S(d) = 6$ оказалась здесь наименьшей, то отмечаем вершину $d$ и закрашиваем дугу $(c,d)$, определяющую эту величину $S(d)$.

Получили, что $x = d$. Теперь по формуле вычисляем величины:

Так как величина $S(b) = 7$ меньше величины $S(t)$, то на этом шаге помечаем вершину $b$ и закрашиваем дугу $(c,b)$, соответствующую выбранному кратчайшему расстоянию.

И теперь последняя итерация алгоритма. Здесь $x = b$ и расстояние

Наконец, вершина $t$ достигнута. Отмечаем её и закрашиваем кратчайший путь, ведущий к ней на этом шаге – дугу $(d,t)$.

В итоге, после применения алгоритма Дейкстры, мы получили дерево кратчайших путей, состоящее из дуг $(s,c), (s,a), (c,d), (c,b)$ и $(d,t)$:

Рисунок 2. Дерево кратчайших путей. Автор24 — интернет-биржа студенческих работ

Из них единственный кратчайший путь, соединяющий вершину $s$ с вершиной $t$, проходит по дугам $(s,c), (c,d), (d,t)$ и имеет длину $2 + 4 + 2 = 8$.

Пошаговое описание алгоритма Дейкстры

Теперь запишем в общей форме те действия, которые были выполнены в примере при отыскании кратчайшего пути. Это позволит в дальнейшем применять данный алгоритм для решения любой задачи такого же типа.

Перечислим шаги алгоритма Дейкстры по пунктам:

На графе каждой вершине $y$ ставится в соответствие число $S(y)$, которое вычисляется как длина условно кратчайшего пути из начальной точки $s$ в вершину $y$. При этом рассматриваются только пути, проходящие через уже помеченные вершины. Изначально полагается, что $S(s) = 0$ и $S(y) = ∞$ для любой (отличной от $s$) вершины $y$. Отмечается вершина $s$, и поэтому переменная $x = s$.
Для каждой неотмеченной вершины $y$ заданного графа пересчитывается величина $S(y)$ по следующей формуле: $S(y) = min\$, где $x$ – промежуточная вершина, отмеченная на предыдущем шаге. Данная формула позволяет выбрать наиболее короткий путь от начальной точки графа до нужной вершины, сравнивая величину пути $S(y)$ с длиной пути, составленного из нескольких дуг и включающего при этом помеченную вершину $x$.

Далее возможны следующие варианты:

Если $S(y) = ∞$ для всех неотмеченных вершин $y$, то отсутствуют пути из $s$ в оставшиеся вершины графа и требуется закончить процедуру алгоритма.
Иначе пометить на графе ту вершину $y$, для которой величина $S(y)$ оказалась минимальной, а также закрасить дугу, оптимально приводящую в эту вершину $y$. Далее полагаем, что $x = y$.

Если оказалось, что $x = t$, то алгоритм завершён, и в результате его применения найден искомый кратчайший путь (это единственный путь из вершины $s$ в вершину $t$, который в ходе выполнения алгоритма получился на графе закрашенным). Иначе требуется перейти к пункту 2 алгоритма и снова повторять его действия до тех пор, пока не будет получен кратчайший путь, соединяющий вершины $s$ и $t$.

Напомним, что данный метод поиска кратчайшего пути применим только для графов с неотрицательными весами дуг.

Обобщение алгоритма Дейкстры на случай, когда некоторым из его дуг соответствуют отрицательные весовые коэффициенты, получило название алгоритма Беллмана-Форда.

Алгоритм Дейкстры позволяет нам найти кратчайший путь между любыми двумя вершинами графа.

Он отличается от минимального остовного дерева тем, что кратчайшее расстояние между двумя вершинами может не включать все вершины графа.

Как работает алгоритм Дейкстры

Алгоритм Дейкстры работает на том основании, что любой подпуть B -> D кратчайшего пути A -> D между вершинами A и D также является кратчайшим путем между вершинами B и D.

Дейкстра использовал это свойство в противоположном направлении, т.е. мы переоцениваем расстояние каждой вершины от начальной вершины. Затем мы посещаем каждый узел и его соседей, чтобы найти кратчайший подпуть к этим соседям.

Пример алгоритма Дейкстры

Проще начать с примера, а затем подумать об алгоритме.

Алгоритм Дейкстры. Псевдокод.

Нам нужно сохранять расстояние пути каждой вершины. Мы можем сохранить его в массиве размера v, где v - количество вершин.

Нам также хотелось бы получить кратчайший путь, а не только знать его длину. Для этого мы сопоставляем каждую вершину с последней обновленной длиной пути.

Как только алгоритм закончен, мы можем вернуться от вершины назначения к исходной вершине, чтобы найти путь.

Очередь с минимальным приоритетом может использоваться для эффективного получения вершины с наименьшим расстоянием пути.

Код для алгоритма Дейкстры

Реализация алгоритма Дейкстры в C ++ приведена ниже. Сложность кода может быть улучшена, но абстракции удобны для связи кода с алгоритмом.

Инициализация

Метка самой вершины 1 полагается равной 0, метки остальных вершин – недостижимо большое число (в идеале — бесконечность). Это отражает то, что расстояния от вершины 1 до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные.

Первый шаг

Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6. Обходим соседей вершины по очереди.

Первый сосед вершины 1 – вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1 (значению её метки) и длины ребра, идущего из 1-й во 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2 (10000), поэтому новая метка 2-й вершины равна 7.

Аналогично находим длины пути для всех других соседей (вершины 3 и 6).

Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит. Вершина 1 отмечается как посещенная.

Второй шаг

Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.

Вершина 1 уже посещена. Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9, а 9 Реализация на C++

// Восстановление пути
int ver[SIZE]; // массив посещенных вершин
int end = 4; // индекс конечной вершины = 5 - 1
ver[0] = end + 1; // начальный элемент - конечная вершина
int k = 1; // индекс предыдущей вершины
int weight = d[end]; // вес конечной вершины

while (end != begin_index) // пока не дошли до начальной вершины
for ( int i = 0; i // просматриваем все вершины
if (a[i][end] != 0) // если связь есть
int temp = weight - a[i][end]; // определяем вес пути из предыдущей вершины
if (temp == d[i]) // если вес совпал с рассчитанным
< // значит из этой вершины и был переход
weight = temp; // сохраняем новый вес
end = i; // сохраняем предыдущую вершину
ver[k] = i + 1; // и записываем ее в массив
k++;
>
>
>
// Вывод пути (начальная вершина оказалась в конце массива из k элементов)
printf( "\nВывод кратчайшего пути\n" );
for ( int i = k - 1; i >= 0; i--)
printf( "%3d " , ver[i]);
getchar(); getchar();
return 0;
>

Результат выполнения

Алгоритм Дейкстры позволяет найти кратчайший путь между двумя любыми вершинами графа (или кратчайший путь сети между заданным исходным и любым другим узлом).

Граф — это совокупность двух множеств: точек (называются вершинами) и путей между ними (изображаются линиями и называются рёбрами).

Алгоритм Дейкстры применяется в жизни. Например, можно использовать графы для моделирования транспортной сети, где точки (вершины) являются объектами, которые отправляют или получают посылки/продукты (места, что водитель должен посетить), а рёбра (линии) представляют собой соединяющие их дороги:

Графы могут быть двух типов:

направленный граф: если для каждой пары узлов можно сделать переход от одного узла к другому только в определённом направлении; для обозначения такого графа используются стрелки вместо простых линий (пример из жизни: когда на дороге есть только одностороннее движение);
ненаправленный граф: если для каждой пары узлов можно сделать переход от одного к другому в обоих направлениях (пример из жизни: когда на дороге есть двустороннее движение).

Пример

Рассмотрим представленный выше пример:

Алгоритм произведёт кратчайший путь от узла 0 ко всем остальным узлам графа.

Для этого графа мы будем предполагать, что вес рёбер (вес или стоимость всегда являются неотрицательными, т.е. ≥ 0; это цифра возле каждой линии) представляет собой расстояние между двумя узлами:

Мы найдём кратчайший путь от узла 0 к узлу 1, потом к узлу 2, потом к узлу 3 и т. д. для каждого узла в графе.

Этот граф также можно представить в виде матрицы:

Таблица: слева "выходит из", сверху "куда направляется", и выставляем "вес" (пример: из "0" идёт в "1" с весом "7", из "0" идёт в "2" с весом "5", и больше из 0 не выходит ничего).

Если можно идти из одного узла в другой и обратно, это указывается в матрице (например: из 2 в 1 с весом 3 И из 1 в 2 с весом 3).

Пошаговый процесс нахождения минимального пути

Шаг 0. В этом примере исходным узлом будет узел 0 (т.к. расстояние от исходного узла до самого себя равно 0; но исходным узлом может быть любой узел, который вы выберете).

Шаг 1. Для первоначального представления расстояния от исходного узла до всех остальных узлов мы используем символ бесконечности, т.к. оно ещё не определено:

Делаем такой список узлов с расстояниями:

Расстояние:

Мы начали с узла 0, значит, отмечаем этот узел как посещённый на диаграмме и вычёркиваем его из списка непосещённых узлов (дистанцию, которая равна нулю, уже обозначили).

Шаг 2. Теперь проверяем расстояние от узла 0 до соседних с ним узлов. Как это видно на картинке, это узлы 1 и 2 (см. красные линии), это наши возможные пути:

Путь 1 = 7, путь 2 = 5, т.к. путь 2 короче (дешевле), то выберем его.

Рассматриваем дальнейшие пути/узлы:

путь от 2 до 1 равняется 3 (5 + 3 = 8, можно возле "1" поставить простым карандашом "8"),
путь от 2 до 4 равняется 4 (5 + 4 = 9, можно возле "4" поставить простым карандашом "9").

Однако существует прямой путь из 0 в узел 1, который равняется 7, а 7

Остались непосещёнными 3 и 4.

Непосещённый сосед 2 – это 4 (мы его ещё не посетили, мы только посчитали), в него можно попасть 5 + 4 = 9, ставим 9.

Непосещённый сосед 1 – это 3, в него можно попасть через:

0-1-3, это 7 + 5 = 12 (т.е. идём из 0 к 1 и потом к 3, и этот путь равен 12)
0-2-4-3 это 9 + 6 = 15 (идём из 0 к 2, потом к 4 и потом к 3, и этот путь равен 15)
0-2-1-3 это 5 + 3 + 5 = 13 (идём из 0 к 2, потом к 1 и потом к 3, и этот путь равен 13)

Естественно выбираем самый короткий путь (равный 12).

Путь 4 тоже оставляем тот, который был выбран, т.к. более короткого не видно (путь через 3 равен 12 + 6 = 18), ставим его посещённым.

Так как непосещённых узлов нет, всё готово!

Расстояние:

Минимальное расстояние каждого узла, что мы нашли, представляет собой минимальное расстояние от этого узла до узла 0 (мы его выбрали в начале в качестве начального узла).

Минимальное остовное дерево

Ещё существует метод "Минимальное остовное дерево", и эти процессы часто путаются. Однако алгоритм Дейкстры отличается от метода Минимального остовного дерева тем, что кратчайшее расстояние между двумя вершинами может не включать все вершины графа; т.е. в алгоритме Дейкстры все вершины должны быть посещены.

Из многих алгоритмов поиска кратчайших маршрутов на графе, на Хабре я нашел только описание алгоритма Флойда-Уоршалла. Этот алгоритм находит кратчайшие пути между всеми вершинами графа и их длину. В этой статье я опишу принцип работы алгоритма Дейкстры, который находит оптимальные маршруты и их длину между одной конкретной вершиной (источником) и всеми остальными вершинами графа. Недостаток данного алгоритма в том, что он будет некорректно работать если граф имеет дуги отрицательного веса.

Для примера возьмем такой ориентированный граф G:

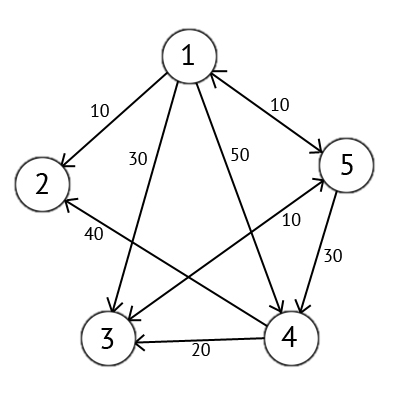
Этот граф мы можем представить в виде матрицы С:

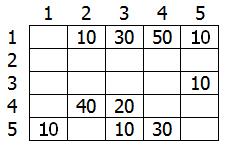
Возьмем в качестве источника вершину 1. Это значит что мы будем искать кратчайшие маршруты из вершины 1 в вершины 2, 3, 4 и 5.
Данный алгоритм пошагово перебирает все вершины графа и назначает им метки, которые являются известным минимальным расстоянием от вершины источника до конкретной вершины. Рассмотрим этот алгоритм на примере.

Присвоим 1-й вершине метку равную 0, потому как эта вершина — источник. Остальным вершинам присвоим метки равные бесконечности.

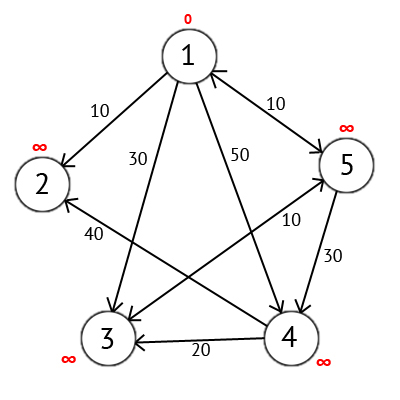
Далее выберем такую вершину W, которая имеет минимальную метку (сейчас это вершина 1) и рассмотрим все вершины в которые из вершины W есть путь, не содержащий вершин посредников. Каждой из рассмотренных вершин назначим метку равную сумме метки W и длинны пути из W в рассматриваемую вершину, но только в том случае, если полученная сумма будет меньше предыдущего значения метки. Если же сумма не будет меньше, то оставляем предыдущую метку без изменений.

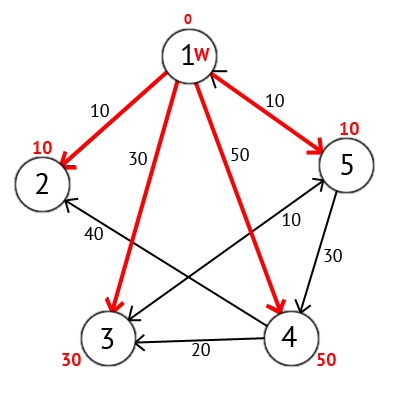
После того как мы рассмотрели все вершины, в которые есть прямой путь из W, вершину W мы отмечаем как посещённую, и выбираем из ещё не посещенных такую, которая имеет минимальное значение метки, она и будет следующей вершиной W. В данном случае это вершина 2 или 5. Если есть несколько вершин с одинаковыми метками, то не имеет значения какую из них мы выберем как W.

Мы выберем вершину 2. Но из нее нет ни одного исходящего пути, поэтому мы сразу отмечаем эту вершину как посещенную и переходим к следующей вершине с минимальной меткой. На этот раз только вершина 5 имеет минимальную метку. Рассмотрим все вершины в которые есть прямые пути из 5, но которые ещё не помечены как посещенные. Снова находим сумму метки вершины W и веса ребра из W в текущую вершину, и если эта сумма будет меньше предыдущей метки, то заменяем значение метки на полученную сумму.

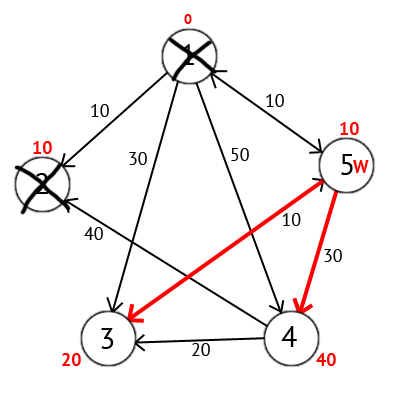
Исходя из картинки мы можем увидеть, что метки 3-ей и 4-ой вершин стали меньше, тоесть был найден более короткий маршрут в эти вершины из вершины источника. Далее отмечаем 5-ю вершину как посещенную и выбираем следующую вершину, которая имеет минимальную метку. Повторяем все перечисленные выше действия до тех пор, пока есть непосещенные вершины.

Выполнив все действия получим такой результат:

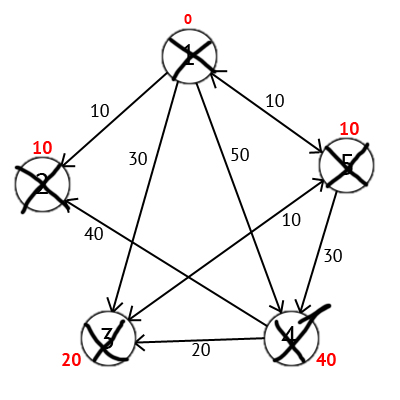
Зная что в каждом элементе вектора Р записана последняя промежуточная вершина на пути между источником и конечной вершиной, мы можем получить и сам кратчайший маршрут.

Читайте также: