Векторы на плоскости конспект
Обновлено: 07.07.2024
Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.
Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.
· Вектор — это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А - начало вектора, а, В — его конец, то вектор обозначается символом или .
· Вектор (у него начало в точке В, а конец в точке А) называется противоположным вектору . Вектор, противоположный вектору , обозначается .
· Длинойили модулемвектора называется длина отрезка и обозначается .
· Вектор, длина которого равна нулю, называется нулевым вектороми обозначается . Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называется единичнымвектором и обозначается через . Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается .
· Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают || .
Коллинеарные векторы могут быть направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным любому вектору.
· Два вектора и называются равными ( = ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку пространства.
· Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Если среди трех поизвольных векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
2. Линейные операции над векторами
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Пусть и — два произвольных вектора. Возьмем произвольную точку О и построим вектор = . От точки А отложим вектор .
· Вектор , соединяющий начало первого вектора с концом второго, называется суммойвекторов и : (см. рис. 1).
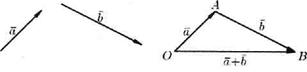
Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелограмма(см. рис. 2).
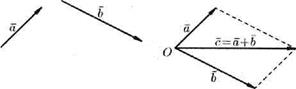
На рисунке 3 показано сложение трех векторов , и .
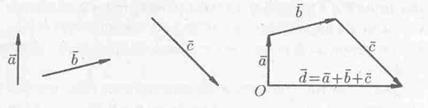
Получившийся многоугольник называют векторным многоугольником; если суммируемые вектора образуют замкнутый многоугольник, то их сумма равна нулю.
· Под разностьювекторов и понимается вектор = - такой, что + = (см. рис. 4).

Отметим, что в параллелограмме, построенном на векторах и , одна направленная диагональ является суммой векторов и , а другая — разностью (см. рис. 5).
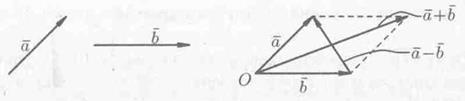
Можно вычитать векторы по правилу: , т. е. вычитание векторов заменить сложением вектора с вектором, противоположным вектору .

· Произведением вектора на скаляр (число) λ называется вектор λ· (или ·λ), который имеет длину |λ|·| |, коллинеарен вектору , имеет направление вектора , если λ > 0 и противоположное направление, если λ
3. Проекция вектора на ось
Пусть в пространстве задана ось l, т. е. направленная прямая.
Проекцией точки Мна ось l называется основание M1 перпендикуляра ММ1, опущенного из точки на ось.
Точка M1 есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).
Если точка М лежит на оси l, то проекция точки М на ось совпадает с М.
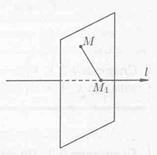
Рис. 7
Пусть — произвольный вектор ( ≠ ). Обозначим через А1 и В1 проекции на ось l соответственно начала А и конца В вектора и рассмотрим вектор .
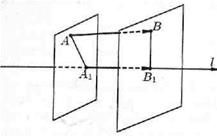
· Проекцией вектора на ось l называется положительное число | |, если вектор и ось l одинаково направлены и отрицательное число - | |, если вектор и ось l противоположно направлены (см. рис. 8). Если точки А1 и В1 совпадают ( = 0), то проекция вектора равна 0.
Проекция вектора на ось l обозначается так: прl . Если = или , то прl = 0.
Угол φ между вектором и осью l (или угол между двумя векторами) изображен на рисунке 9. Очевидно, 0 ≤ φ ≤ π.
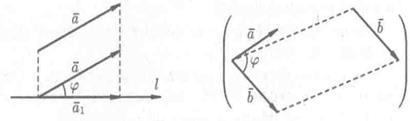
Рассмотрим основные свойства проекций.
С 1. Проекция вектора на ось l равна произведению модуля вектора на косинус угла φ между вектором и осью, т. е. прl = | |• cos φ.
ü Если φ π/2 (φ ≤ π), то прl = -| | = -| |·cos(π-φ) = | | · cos φ (см. рис. 10).
ü Если φ = π/2, то прl = 0 = |a|cos φ.
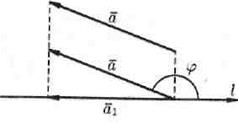
Рис. 10.
Следствие 1.Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол — прямой.
Следствие 2.Проекции равных векторов на одну и ту же ось равны между собой.
С 2.Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.
Пусть, например, = + + . Имеем прl = +| | = +| | + | | - | |, т. е. прl ( + + ) = прl + прl + прl (см. рис. 11).
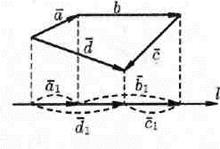
Рис. 11.
С 3. При умножении вектора на число λ его проекция на ось также умножается на это число, т. е. прl (λ· ) = λ· прl
При λ > 0 имеем прl (λ· ) = |λ |·сos φ = λ·| |·cos φ = λ· прl· .
При λ 2 = | | 2 · cos 2 α + | | 2 · cos 2 β + | | 2 · cos 2 γ.
Сократив на | | 2 ≠ 0, получим соотношение:
cos 2 α + cos 2 β + cos 2 γ = 1,
т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координатами единичного вектора являются числа cos α, cos β, cos γ, т. е. = (cos α; cos β; cos γ)
Итак, задав координаты вектора, всегда можно определить его модуль и направление, т. е. сам вектор.
5. Действия над векторами, заданными проекциями
Пусть векторы = (ах; ау; az) и = (bх; bу; bz) заданы своими проекциями на оси координат Ох, Оу, Oz или, что то же самое
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
1. Основные понятия
Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.
Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.
· Вектор — это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А - начало вектора, а, В — его конец, то вектор обозначается символом или .
· Вектор (у него начало в точке В, а конец в точке А) называется противоположным вектору . Вектор, противоположный вектору , обозначается .
· Длинойили модулемвектора называется длина отрезка и обозначается .
· Вектор, длина которого равна нулю, называется нулевым вектороми обозначается . Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называется единичнымвектором и обозначается через . Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается .
· Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают || .
Коллинеарные векторы могут быть направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным любому вектору.
· Два вектора и называются равными ( = ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку пространства.
· Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Если среди трех поизвольных векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
2. Линейные операции над векторами
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Пусть и — два произвольных вектора. Возьмем произвольную точку О и построим вектор = . От точки А отложим вектор .
· Вектор , соединяющий начало первого вектора с концом второго, называется суммойвекторов и : (см. рис. 1).
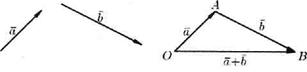
Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелограмма(см. рис. 2).

На рисунке 3 показано сложение трех векторов , и .

Получившийся многоугольник называют векторным многоугольником; если суммируемые вектора образуют замкнутый многоугольник, то их сумма равна нулю.
· Под разностьювекторов и понимается вектор = - такой, что + = (см. рис. 4).

Отметим, что в параллелограмме, построенном на векторах и , одна направленная диагональ является суммой векторов и , а другая — разностью (см. рис. 5).
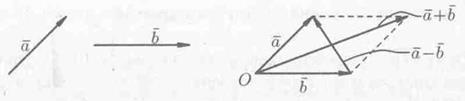
Можно вычитать векторы по правилу: , т. е. вычитание векторов заменить сложением вектора с вектором, противоположным вектору .
· Произведением вектора на скаляр (число) λ называется вектор λ· (или ·λ), который имеет длину |λ|·| |, коллинеарен вектору , имеет направление вектора , если λ > 0 и противоположное направление, если λ π/2 (φ ≤ π), то прl = -| | = -| |·cos(π-φ) = | | · cos φ (см. рис. 10).
ü Если φ = π/2, то прl = 0 = |a|cos φ.

Рис. 10.
Следствие 1.Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол — прямой.
Следствие 2.Проекции равных векторов на одну и ту же ось равны между собой.
С 2.Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.
Пусть, например, = + + . Имеем прl = +| | = +| | + | | - | |, т. е. прl ( + + ) = прl + прl + прl (см. рис. 11).

Рис. 11.
С 3. При умножении вектора на число λ его проекция на ось также умножается на это число, т. е. прl (λ· ) = λ· прl
При λ > 0 имеем прl (λ· ) = |λ |·сos φ = λ·| |·cos φ = λ· прl· .
При λ 2 = | | 2 · cos 2 α + | | 2 · cos 2 β + | | 2 · cos 2 γ.
Сократив на | | 2 ≠ 0, получим соотношение:
cos 2 α + cos 2 β + cos 2 γ = 1,
т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координатами единичного вектора являются числа cos α, cos β, cos γ, т. е. = (cos α; cos β; cos γ)
Итак, задав координаты вектора, всегда можно определить его модуль и направление, т. е. сам вектор.
5. Действия над векторами, заданными проекциями
Пусть векторы = (ах; ау; az) и = (bх; bу; bz) заданы своими проекциями на оси координат Ох, Оу, Oz или, что то же самое
Вектором на плоскости называется направленный отрезок прямой, причем один из концов отрезка (точка) является началом вектора, а второй – его концом (рис. 1).

![]()
. Также для обозначения векторов используются строчные латинские буквы:
![]()
Нулевой вектор
![]()
называется вектор, у которого начало совпадает с концом (рис. 1).
![]()
придают любое направление на плоскости.
Длинойили модулем \right|" width="38" height="24" />
вектора " width="30" height="16" />
называется неотрицательное число, равное длине отрезка , который задает вектор.
![]()
равна нулю.
![]()

Коллинеарные и неколлинеарные векторы на плоскости
Два вектора на плоскости называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2). В противном случае векторы называются неколлинеарными.
![]()
коллинеарен любому другому вектору плоскости.
Сонаправленные и противоположно направленные векторы на плоскости
Два коллинеарных вектора и " width="8" height="16" />
называются сонаправленными, если их направления совпадают. Сонаправленные векторы обозначаются следующим образом: " width="47" height="20" />
. Два коллинеарные вектора и " width="8" height="16" />
называются противоположно направленными, если их направления противоположны. Обозначение " width="47" height="20" />
.
![]()
сонаправлен с любым другим вектором плоскости.

Два вектора плоскости называются равными, если они сонаправлены и их длины равны (рис. 3):
![]()

Вектор называется противоположным к вектору , если эти векторы противоположно направлены и их длины равны.
Отложим от некоторой точки на плоскости два произвольных вектора и " width="8" height="16" />
(рис. 4). Лучи, исходящие из этой точки образуют угол , который называется углом между векторами и " width="8" height="16" />
:
![]()

Угол между сонаправленными векторами равен " width="16" height="14" />
(или нулю радиан), а угол между противоположно направленными векторами – " width="33" height="15" />
(или радиан).
Два вектора и " width="8" height="16" />
называются ортогональными (или перпендикулярными), если угол между ними равен " width="25" height="14" />
(>\right.\kern-\nulldelimiterspace> 2>" width="30" height="18" />
радиан) (рис. 5).
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Конспект урока по геометрии.
Подготовила: учитель математики Анна Николаевна
проверить знания основных понятий и формул по векторам;
формировать навыки в умении решать ключевые задачи по данной теме, применяя известные понятия, свойства и формулы по векторам;
способствовать развитию умения ориентироваться в теоретическом материале, выделять главное, необходимое для решения задач;
формировать навыки самообразовательной деятельности;
воспитание культуры устной и письменной математической речи;
умения общаться, толерантности отношений, интереса к предмету.
Тип урока: урок обобщения и систематизации знаний.
Организационный момент.
Мотивация учебной деятельности.
3. Постановка целей и задач.
Итак, цели и задачи поставлены, приступим к работе по их выполнению.
4. Работа по теме урока.
- Начнём урок с основных понятий связанных с этой темой. Понятие вектора, изображение и обозначение, нулевой вектор, коллинеарные векторы, одинаково направленные, равные, противоположно направленные, противоположные векторы, характеристические данные: длина и направление.
- Давайте заполним таблицу, в которой вы должны определить соответствие между понятиями и формулами с пояснениями.
Б) ( )
В) ( )
Г)
Умножение вектора на число
Д) ( )
Ж) cos( )
Скалярное произведение векторов.
З) ( )
И)
1 - В; 2 - Г ; 3 - Д ; 4 - Б ; 5 - З ; 6 - И ; 7 - Е ; 8 - А, Ж .
- Чем отличается результат действий сложения, вычитания, умножения вектора на число от результата скалярно произведения?
- Как определить вид треугольника с помощью векторов?
- Как доказать, что данный четырехугольник параллелограмм?
- Как доказать, что параллелограмм – является ромбом?
- Как найти неизвестные координаты вершины параллелограмма?
- Как определить вид треугольника по углам и сторонам?
5. Закрепление изученного материала.
Мы с вами вспомнили основные понятия и формулы и теперь приступим к решению задач. Сейчас небольшая разминка. Решаем тестовые задания.
Найти координаты вектора , если А(3;-4), В(0;2).
Вычислить модуль вектора (-1;4).
А) 3; Б) 5; В) ; Г) .
При каком значении х векторы (4;2) и (х;-4) коллинеарные?
А) -2; Б) 2; В) -8; Г) 8.
Вычислить скалярное произведение векторов (5;-4) и (2;3)
А) -4; Б) 4; В) 2; Г) -2.
При каком значении n векторы (n;3) и (-3;3) перпендикулярны?
А) -3; Б) 3; В) -2; Г) 2
Определить вид угла между векторами (-3;5) и (-4;-2).
А) тупой; Б) острый; В) прямой; Г) определить невозможно.
Выполняем взаимопроверку. 1-В; 2-В; 3-В; 4-Г; 5-Б; 6-Б.
- А теперь решим текстовую задачу.
Даны координаты вершин пирамиды АВС D :
А (2;3,1), В (6,1;-1), С (4,8;-9), D (2;-1,2).
- Записать векторы АВ,АС, А D в системе орт i , j , k и найти модули этих векторов.
Определение. Вектор - это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины. (рис.1)
 |
| рис. 1 |
Обозначение вектора
Вектор началом которого есть точка А, а концом - точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .
Длина вектора
Определение. Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB .
Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.
Нулевой вектор
Нулевой вектор обычно обозначается как 0 .
Длина нулевого вектора равна нулю.
Коллинеарные вектора
Определение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).
 |
| рис. 2 |
Сонаправленные вектора
Определение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a ↑↑ b (рис. 3).
 |
| рис. 3 |
Противоположно направленные вектора
Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a ↑↓ b (рис. 4).
 |
| рис. 4 |
Компланарные вектора
Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).
 |
| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Равные вектора
Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
 |
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b , если a ↑↑ b и | a | = | b |.
Единичный вектор
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Читайте также:

