Прямая на плоскости конспект

Обновлено: 07.07.2024

Прямые в пространстве. Прямая и плоскость в пространстве.

Вложение	Размер
Прямые в пространстве. Прямая и плоскость в пространстве.	185 КБ

Предварительный просмотр:

Теоретическое занятие по теме:

Прямые в пространстве. Прямая и плоскость в пространстве.

Маршрутный лист занятия:

1. Запишите конспект в тетрадь. Текст, выделенный желтым цветом, конспектировать НЕ нужно, его необходимо внимательно прочитать и разобрать.

Основные понятия стереометрии

Простейшими и, можно сказать, основными фигурами в пространстве являются точки, прямые и плоскости . Наряду с этими фигурами мы будем рассматривать так называемые геометрические тела и их поверхности . Представление о геометрических телах дают окружающие нас предметы.

Основными понятиями стереометрии являются точка, прямая и плоскость, которые являются идеализациями объектов реального пространства.

Прямая является идеализацией тонкой натянутой нити, края стола прямоугольной формы. По прямой распространяется луч света.

Плоскость является идеализацией ровной поверхности воды, поверхности стола, доски, зеркала и т. п.

Точки будем обозначать прописными латинскими буквами A, B, C,…., прямые — строчными латинскими буквами а, Ь, с , . плоскости — греческими … .

Точки, прямые и плоскости будем изображать, как показано на рисунке 1.

Рис. 1

Обратим внимание на то, что прямая является бесконечной, а мы изображаем лишь конечный участок прямой — отрезок, который можно продолжать в обе стороны. Плоскость также является бесконечной, и мы будем изображать лишь ее конечный участок.

А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

А
В (точки А, В, С лежат в плоскости )
С

А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

АB
Прямая АВ лежит в плоскости

Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.

а = М
Прямая а и плоскость пересекаются в точке М.

А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

= a
и пересекаются по прямой а.

Следствие 1. Через прямую a и не лежащую на ней точку A проходит плоскость, и притом только одна.

Рис. 6
Следствие 2. Через две пересекающиеся прямые a и b проходит плоскость, и притом только одна.

Взаимное расположение прямых в пространстве

Возможны три случая взаимного расположения двух прямых в пространстве (Рис. 8):

а) прямые пересекаются, т. е. имеют только одну общую точку (рис. а);

б) прямые параллельны, т. е. лежат в одной плоскости и не пересекаются (рис.б);

в) прямые скрещивающиеся, т. е. не лежат в одной плоскости (рис. в).

Обязательно запомнить обозначения!

Пересекающиеся прямые обозначают так: a b

Параллельные прямые обозначают так: a b

Скрещивающиеся прямые обозначают так: a ∸ b

Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Параллельность прямой и плоскости.

Если две точки прямой лежат в данной плоскости, то по аксиоме 2 вся прямая лежит в этой плоскости. Отсюда следует, что возможны три случая взаимного расположения прямой и плоскости в пространстве:

а) прямая лежит в плоскости

б) прямая и плоскость имеют только одну общую точку, т. е. пересекаются

в) прямая и плоскость не имеют ни одной общей точки.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Параллельность прямой а и плоскости α обозначается так: а ∥ 𝛼 . Наглядное представление о прямой, параллельной плоскости, дают натянутые троллейбусные или трамвайные провода — они параллельны плоскости земли. Другой пример дает линия пересечения стены и потолка — эта линия параллельна плоскости пола.

Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Доказательство. Рассмотрим плоскость а и две параллельные прямые а и b, расположенные так, что прямая b лежит в плоскости а, а прямая а не лежит в этой плоскости (Рис. 9).

Докажем, что а ∥ 𝛼 .. Допустим, что это не так. Тогда прямая а пересекает плоскость а, а значит, по лемме о пересечении плоскости параллельными прямыми прямая b также пересекает плоскость а. Но это невозможно, так как прямая

b лежит в плоскости а. Итак, прямая а не пересекает плоскость а, поэтому она параллельна этой плоскости. Теорема доказана.

Запишем еще два утверждения , которые часто используются при решении задач.

1°. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

2°. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Параллельные прямые в пространстве.

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Параллельность прямых а и b обозначается так: а ∥ 𝑏 . Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Доказательство. Рассмотрим прямую а и точку М, не лежащую на этой прямой (Рис. 1о). Через прямую а и точку М проходит плоскость, и притом только одна (п. 3). Обозначим эту плоскость буквой а. Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т. е. должна лежать в плоскости а. Но в плоскости а, как известно из курса планиметрии, через точку М проходит прямая, параллельная прямой а, и притом только одна. На рисунке эта прямая обозначена буквой b. Итак, b - единственная прямая, проходящая через точку M параллельно прямой а. Теорема доказана.

Перпендикулярные прямые в пространстве.

Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°. Перпендикулярность прямых а и b обозначается так: a ⊥ 𝑏 . Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.

Лемма. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Окружающая нас обстановка дает много примеров, иллюстрирующих перпендикулярность прямой и плоскости. Не покосившийся телеграфный столб стоит прямо, т. е. перпендикулярно к плоскости земли. Так же расположены колонны здания по отношению к плоскости фундамента, линии пересечения стен по отношению к плоскости пола и т. д.

Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

Теорема (O). Если две прямые перпендикулярны к плоскости, то они параллельны.

Признак перпендикулярности прямой и плоскости.

Как проверить, перпендикулярна ли данная прямая к данной плоскости? Этот вопрос имеет практическое значение, например, при установке мачт, колонн зданий и т. д., которые нужно поставить прямо, т. е. перпендикулярно к той плоскости, на которую они ставятся. Оказывается, что для этого нет надобности проверять перпендикулярность по отношению к любой прямой, как о том говорится в определении, а достаточно проверить перпендикулярность лишь к двум пересекающимся прямым, лежащим в плоскости. Это вытекает из следующей теоремы, выражающей признак перпендикулярности прямой и плоскости.

Теорема. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Перпендикуляр и наклонная

Рассмотрим плоскость α и точку А, не лежащую в этой плоскости. Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью а (Рис. 11).

Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости а, а точка Н — основанием перпендикуляра. Отметим в плоскости а какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости а, а точка М — основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость а. Сравним перпендикуляр АН и наклонную AM: в прямоугольном треугольнике АМН сторона АН — катет, а сторона AM— гипотенуза, поэтому АН

Когда мы говорим, что некоторый предмет, например лампочка уличного фонаря, находится на такой-то высоте, скажем, 6 м от земли, то имеем в виду, что расстояние от лампочки до поверхности земли измеряется по перпендикуляру, проведенному от лампочки к плоскости земли.

Теорема о трех перпендикулярах.

Теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

Доказательство. Обратимся к рисунку, на котором отрезок АН — перпендикуляр к плоскости a, AM —наклонная, а — прямая, проведенная в плоскости а через точку М перпендикулярно к проекции НМ наклонной. Докажем, что a ⊥ AM. Рассмотрим плоскость АМН. Прямая а перпендикулярна к этой плоскости, так как она перпендикулярна к двум пересекающимся прямым АН и МНа ⊥ HM по условию и a ⊥ AH, так как АН ⊥ 𝛼 ). Отсюда следует, что прямая а перпендикулярна к любой прямой, лежащей в плоскости АМН, в частности a ⊥ AM. Теорема доказана.

Эта теорема называется теоремой о трех перпендикулярах, так как в ней говорится о связи между тремя перпендикулярами АН, НМ и AM.

Определение. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.

2. Рассмотрим следующую задачу (записать в тетрадь):

Точка D не лежит в плоскости треугольника ABC, точки М, N и Р — середины отрезков DA, DB и DC соответственно, точка К лежит на отрезке BN. Выясните взаимное расположение прямых: a) ND и АВ; б) РК и ВС; в) MN и АВ; г) МР и АС; д) KN и AC; е) MD и ВС.

Посмотреть видео-разбор, законспектировать.

3. Вопросы для самоконтроля (ответить устно):

Дать определение стереометрии?
Какие основные фигуры в пространстве вы знаете?
Как обозначаются основные фигуры в пространстве (точка, прямая, плоскость)?
Какие аксиомы стереометрии и следствия из них вы знаете?

4. Домашнее задание (письменно):

1. Перечислите известные вам аксиомы стереометрии.

2. Дан куб .

Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.

Прямая на плоскости – понятие

Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.

Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.

Взаимное расположение прямой и точки

На каждой прямой и в каждой плоскости могут быть отмечены точки.

Точки обозначают как большими, так и маленькими латинскими буквами. Например, А и D или a и d .

Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.

Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.

Данное высказывание считается акисомой, поэтому не требует доказательств. Если рассмотреть это самостоятельно, видно, что при существующих двух точках имеется только один вариант их соединения. Если имеем две заданные точки А и В , то прямую, проходящую через них можно назвать данными буквами, например, прямая А В . Рассмотрим рисунок, приведенный ниже.

Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:

Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.

Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.

Краткая запись принадлежности включает в себя использование знаков ∈ и ∉ . Для того, чтобы зафиксировать расположение отрезка относительно заданной прямой, применяют ⊂ . Если в условии дано, что отрезок А Р принадлежит прямой b , значит, и запись будет выглядеть следующим образом: А Р ⊂ b .

Случай принадлежности одновременно трех точек одной прямой имеет место быть. Это верно, когда одна точка лежит между двумя другими. Данное утверждение принято считать аксиомой. Если даны точки А , В , С , которые принадлежат одной прямой, а точка В лежит между А и С , следует, что все заданные точки лежат на одной прямой, так как лежат по обе стороны относительно точки B .

Точка делит прямую на две части, называемые лучами. Имеем аксиому:

Любая точка O , находящаяся на прямой, делит ее на два луча, причем две любые точки одного луча лежат по одну сторону луча относительно точки O , а другие – по другую сторону луча.

Взаимное расположение прямых на плоскости

Расположение прямых на плоскости может принимать вид двух состояний.

Две прямые на плоскости могут совпадать.

Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.

Две прямые на плоскости могут пересекаться.

Данный случай показывает, что имеется одна общая точка, которую называют пересечением прямых. Вводится обозначение пересечение знаком ∩ . Если имеется форма записи a ∩ b = M , то отсюда следует, что заданные прямые a и b пересекаются в точке M .

При пересечении прямых имеем дело образовавшимся углом. Отдельному рассмотрению подвергается раздел пересечения прямых на плоскости с образованием угла в 90 градусов, то есть прямого угла. Тогда прямые называют перпендикулярными. Форма записи двух перпендикулярных прямых такая: a ⊥ b , а это значит, что прямая a перпендикулярна прямой b .

Две прямые на плоскости могут быть параллельны.

Только в том случае, если две заданные прямые не имеют общих пересечений, а, значит, и точек, они параллельны. Используется обозначение, которое можно записать при заданной параллельности прямых a и b : a ∥ b .

Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.

Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.

Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.

Для этого приводим необходимы факторы, доказывающие их взаимное расположение:

если две прямые параллельны третьей, тогда они все параллельны;
если две прямые перпендикулярны третьей, тогда эти две прямые параллельны;
если на плоскости прямая пересекла одну параллельную прямую, тогда пересечет и другую.

Рассмотрим это на рисунках.

Способы задания прямой на плоскости

Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.

Прямая задается при помощи указанных двух точек, расположенных в плоскости.

Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.

Прямая может быть задана через точку и прямую, которой она параллельна.

Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.

Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.

Прямая задается через указанную точку и направляющий вектор.

Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.

Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:

Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.

И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Прямая линия на плоскости

Уравнение линии на плоскости

Как известно, любая точка на плоскости определяется двумя координатами в какой- либо системе координат. Системы координат могут быть различными в зависимости от выбора базиса и начала координат.

Определение. Уравнением линии называется соотношение y = f ( x ) между координатами точек, составляющих эту линию.

Отметим, что уравнение линии может быть выражено параметрическим способом, то есть каждая координата каждой точки выражается через некоторый независимый параметр t .

Характерный пример – траектория движущейся точки. В этом случае роль параметра играет время.

Нахождение координат вектора по координатам начала и конца

В репере рассмотрим две точки плоскости: , .

Каждая координата вектора равна разности соответствующих координат конца и начала этого вектора.

Деление отрезка в данном отношении

Пусть даны координаты концов отрезка , . Пусть точка с неизвестными координатами принадлежит отрезку и делит отрезок в отношении , то есть .

Определение. Отношение , в котором точка делит направленный отрезок , называется простым отношением трех точек.

1) Как видно из формул (1) на прямой АВ не существует точки, делящей отрезок в отношении

2) , если точка М – внутренняя точка отрезка АВ;

3) , если точка М –внешняя точка отрезка АВ;

4) если то М – середина отрезка АВ, тогда из формул (2) следует

Расстояние между двумя точками

Определение. Расстоянием между точками , называется длина отрезка или модуль вектора .

4. Направляющий вектор прямой.

Рассмотрим аффинную систему координат и относительно этой системы рассмотрим прямую линию.

Определение. Направляющим вектором прямой называется не нулевой вектор, коллинеарный данной прямой.

Различные способы задания прямой

1. Каноническое уравнение прямой (уравнение прямой заданной точкой и направляющим вектором)

Из (*) (1) – уравнение прямой

Если то (1`) - каноническое уравнение прямой .

Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Решение: Воспользуемся формулой (1 `).

2. Параметрические уравнения прямой.

Из уравнения (1) , t – множитель пропорциональности

- уравнение прямой в параметрическом виде.

Пример 1. Дано . Записать данное параметрическое уравнение в каноническом виде. Для этого нужно исключить параметр t . - каноническое уравнении.

3. Уравнение прямой, проходящей через две точки.

На прямой возьмем две фиксированные точки .

– уравнение прямой, проходящей через две точки.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Применяя записанную выше формулу, получаем:

Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.

Уравнение прямой имеет вид: ;

Для самостоятельного решения: Составить уравнения прямых, проходящих через точку М(-3, -4) и параллельных осям координат.

4. Уравнение прямой в отрезках.

уравнение прямой в отрезках.

5. Уравнение прямой с угловым коэффициентом.

Пусть дана прямая -направляющий вектор. .

Определение. Угловым коэффициентом прямой называется число равное отношению второй координаты направляющего вектора к первой.

Лемма : Угловой коэффициент не зависит от направляющего вектора.

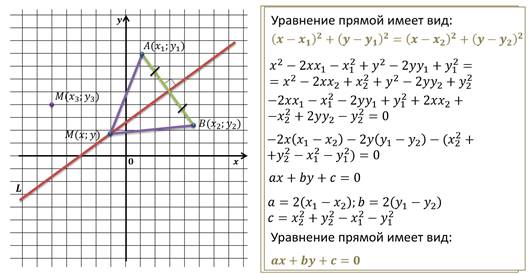
6. Общее уравнение прямой.

Теорема 1 . Всякая прямая является алгебраической линией второго порядка.

Обратно : Линия на плоскости, заданная в аффинной системе координат уравнением есть прямая. Направляющий вектор этой прямой имеет координаты (-В, А) или (В, -А).

Вывод : Всякая алгебраическая линия первого порядка есть прямая (6) – общее уравнение прямой, А, В – коэффициенты при текущих координатах, С - свободный член.

7. Уравнение прямой, заданной точкой и нормальным вектором.

Определение. Нормальным вектором прямой называется любой не нулевой вектор ортогональный данной прямой.

Определение. Прямая, перпендикулярная данной прямой, называется нормальной данной прямой.

Направляющим вектором нормали является нормальный вектор данной прямой.

– уравнение прямой, заданной точкой и нормальным вектором.

Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Составим при =3 и =-1 уравнение прямой:

Взаимное расположение двух прямых

Рассмотрим в аффинной системе координат две прямые, заданные уравнениями:

Две прямые на плоскости пересекаются тогда и только тогда, когда коэффициенты уравнений при х и у не пропорциональны.

Две прямые совпадают тогда и только тогда, когда все коэффициенты в их уравнениях пропорциональны.

Две прямые параллельны тогда и только тогда, когда коэффициенты в их уравнениях при х и у пропорциональны, а свободные члены не пропорциональны.

Угол между двумя прямым

Определение. Углом между данными прямыми называется угол, который не больше .

Определение. Направленным углом между прямыми , взятыми в указанном порядке на ориентированной плоскости называется угол от направляющего вектора первой прямой до направляющего вектора второй прямой, который не больше .

Расстояние от точки до прямой

Определение. Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из этой точки на прямую.

Пример. Определить угол между прямыми: y = -3 x + 7; y = 2 x + 1.

= -3; k ₂ = 2 tg = ;  =  /4.

Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Находим: k ₁ = 3/5, k ₂ = -5/3 , k ₁ k ₂ = -1 , следовательно, прямые перпендикулярны.

Пример. Даны вершины треугольника А(0; 1), B (6; 5), C (12; -1). Найти уравнение высоты, проведенной из вершины С.

Находим уравнение стороны АВ:

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b .

k = . Тогда y = .

Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: откуда b = 17. Итого: .

Для самостоятельного решения:

Даны стороны треугольника x + y – 6 = 0, 3 x – 5 y + 15 = 0, 5 x – 3 y – 14 = 0. Составить уравнения его высот.

Указание: Сначала следует найти координаты вершин треугольника, как точек пересечения сторон, затем воспользоваться методом, рассмотренном в предыдущем примере.

Геометрический смысл коэффициентов общего уравнения прямой

1. В этом случае уравнение (7) примет вид:

это уравнение прямой, проходящей через начало координат.

2. Тогда уравнение (7) примет вид:

- это уравнение прямой, параллельной оси Направляющий вектор будет иметь координаты

3. Тогда уравнение (7) примет вид:

- это уравнение оси Направляющий вектор будет иметь координаты

4. Тогда уравнение (7) примет вид:

- это уравнение прямой, параллельной оси Направляющий вектор будет иметь координаты

5. Тогда уравнение (7) примет вид:

- это уравнение оси . Направляющий вектор будет иметь координаты

подготовка к ЕГЭ/ОГЭ и ВПР
по всем предметам 1-11 классов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 933 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 683 человека из 75 регионов

Курс повышения квалификации

Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam

Курс добавлен 31.01.2022
Сейчас обучается 24 человека из 17 регионов

ЗП до 91 000 руб.
Гибкий график
Удаленная работа

Дистанционные курсы для педагогов

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 610 739 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

30.01.2017 590
DOCX 247.3 кбайт
3 скачивания
Оцените материал:

Настоящий материал опубликован пользователем Аленина Татьяна Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

40%

Подготовка к ЕГЭ/ОГЭ и ВПР
Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В приграничных пунктах Брянской области на день приостановили занятия в школах

Время чтения: 0 минут

Минтруд предложил упростить направление маткапитала на образование

Время чтения: 1 минута

Рособрнадзор предложил дать возможность детям из ДНР и ЛНР поступать в вузы без сдачи ЕГЭ

Время чтения: 1 минута

Минпросвещения России подготовит учителей для обучения детей из Донбасса

Время чтения: 1 минута

Время чтения: 2 минуты

Отчисленные за рубежом студенты смогут бесплатно учиться в России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Уравнения прямой и линии на плоскости"

· вывести уравнения прямой и произвольной линии на плоскости.

И начнём мы наш урок с повторения уравнения прямой.

В координатной плоскости прямая может располагаться либо вертикально (параллельно оси Oy), горизонтально (параллельно оси Ox) либо быть наклонной к обеим осям.

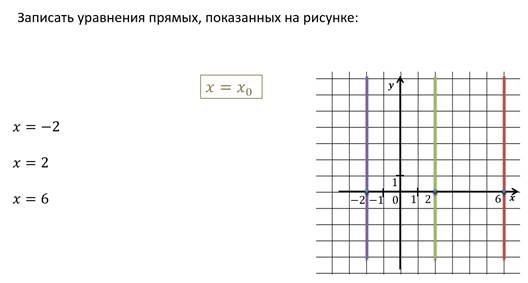
Первым давайте рассмотрим случай, когда прямая параллельна оси Oy.

Возьмём на оси Ox, например, точку с координатой 3 и проведём через эту точку прямую, параллельную оси Oy. Абсцисса любой точки этой прямой равна 3. То есть координаты любой точки этой прямой удовлетворяют уравнению x = 3, а координаты любой точки, которая не лежит на данной прямой не удовлетворяют данному уравнению. Значит, уравнение x = 3 является уравнением прямой параллельной оси Oy и проходящей через точку с координатами (3; 0).

Можно сказать, что произвольная прямая параллельная оси Oy задаётся уравнением:

Ось Oy задаётся уравнением x = 0.

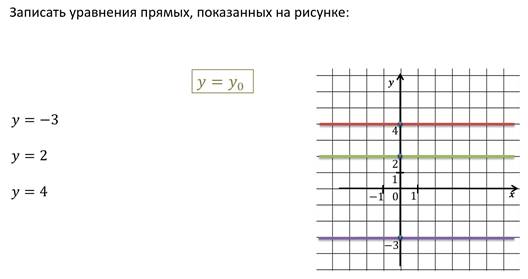
Рассмотрим теперь случай, когда прямая параллельна оси Ox.

Возьмём на оси Oy, например, точку 5 и проведём через неё прямую параллельную оси Ox. Любая точка этой прямой удовлетворяет уравнению y = 5, любая точка, которая не лежит на этой прямой не удовлетворяет этому уравнению, значит, эту прямую задаёт уравнение y = 5.

Можно сказать, что произвольная прямая параллельная оси Ox задаётся уравнением:

Ось Ox задаётся уравнением y = 0.

Теперь рассмотрим случай, когда прямая наклонная к обеим осям.

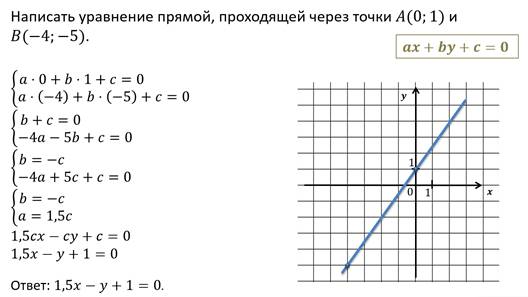
Запишем общее уравнение прямой.

Выразим y через x:

Число k называется угловым коэффициентом прямой.

Отметим, что две параллельные прямые, не параллельные оси Oy имеют одинаковые угловые коэффициенты и если две прямые имеют одинаковые угловые коэффициенты, то эти прямые параллельны. Почему мы говорим о прямых, не параллельных оси Oy? Потому что, мы помним, что уравнение прямых, параллельных оси имеют вид x = x₀, и они все параллельны между собой.

Решим несколько задач.

Решим ещё одну задачу.

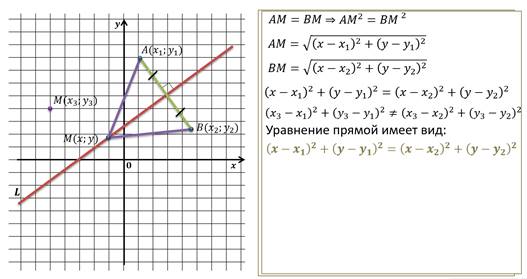
Теперь давайте вспомним как мы вводили понятие уравнения для произвольной линии.

Пусть в декартовой системе координат дана произвольная линия L.

Уравнение с двумя переменными x и y называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

Давайте решим задачу.

Рассмотрим ещё один пример.

Решим ещё одну задачу.

Сегодня на уроке мы с вами повторили уравнения прямой и произвольной линии на плоскости.

Читайте также: