Производная степенной функции 11 класс алимов конспект урока

Обновлено: 05.07.2024

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Приветствовать обучающихся, отметить отсутствующих.

Проверить подготовленность обучающихся к учебному занятию.

Подготовится к учебному занятию.

Проверка выполнения домашнего задания

Ответы на вопросы по домашнему заданию (решение примеров)

Контроль усвоения материала. Фронтальный опрос : Производная. Определение производной

Введение новых понятий.

Определение производной.

Геометрический и физический смыслы.

Ответить на вопросы

Показать д - е задание.

Подготовка обучающихся к работе на основном этапе

Развивающие: - содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать ;

Воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся, повышать мотивацию к изучению математики. Тип урока: комбинированный, включающий освоение новых знаний.

Мобилизирующий момент: Вспомним о степенных функциях. Давайте составим кластер.

Объявление темы урока

Тема Производная степенной функции.

Правила вычисления производных.

Производная степеннной функци.

Производная обратной степенной функции.

Производная корня х.

Подготовить тетради и ручки. Составить кластер.

Алгебра и начала математического анализа.

Формирование новых знаний и способов деятельности

Консультация Правила вычисления производных

Пусть функции и имеют производные в точке . Тогда

1. Константу можно выносить за знак производной.

2. Производная суммы/разности.

Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.

3. Производная произведения.

4. Производная частного.

5. Производная сложной функции.

Производная сложной функции равна производной этой функции по промежуточному аргументу , умноженной на производную от промежуточного аргумента по основному аргументу .

и имеют производные соответственно в точках и . Тогда

(О производной обратной функции)

Если функция непрерывна и строго монотонна в некоторой окрестности точки и дифференцируема в этой точке, то обратная функция имеет производную в точке , причем .

Таблица производных, производные основных элементарных функций

Внимательно слушать консультацию. Записывать важные информации.

Алгебра и начала математического анализа.

Первичная проверка понимания изученного материала

Закрепление новых знаний и способов деятельности

ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ

Формула

Производная степенной функции равна произведению показателя степени и основания в степени на единицу меньше.

Заметим, что в качестве степени может быть как натуральное число , то есть 1, 2, 3, . ; так и любое отрицательное число: - 1, - 2 и т.д., а также и любое дробное, например, 2,34; - 4,1 или , .

Заметим, что если аргумент у степенной функции есть сложная функция (то есть там стоит более сложное выражение, чем просто ), то производную нужно находить по следующей формуле:

Примеры вычисления производной степенной функции

Задание. Найти производную функции

Решение. Искомая производная

По правилам дифференцирования выносим константу за знак производной:

Далее находим производную степенной функции по формуле:

Ответ.

Задание. Вычислить производную функции

Решение. Искомая производная равна:

Далее находим производную по формуле, но учитываем, что основание степени есть что-то более сложное, чем (то есть ищем производную от сложной функции), то умножаем еще все на производную от основания степени:

В первом множителе упрощаем степень, а также находим производную, учитывая тот факт, что производная от суммы равна сумме производных :

Находя производные от степенной функции и от константы, получаем:

Упрощаем полученное выражение:

Ответ.

ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ

Известно свойство степеней, что

Примеры вычисления производной обратной функции

Задание. Найти производную функции

Решение. Искомая производная

Константу - 3 выносим за знак производной (согласно правилам дифференцирования ):

Тогда, согласно формуле получаем:

Или после упрощения

Ответ.

Задание. Вычислить производную функции

Решение. В знаменателе заданной функции стоит функция , то есть

Поэтому необходимо найти производную сложной функции . Для этого находим производную от :

и умножаем на производную от функции :

Производная суммы/разности равна сумме/разности производных. Тогда имеем:

Производная от независимой переменной равна единице: , а производная от единицы, как от константы, равна нулю:

Ответ.

ПРОИЗВОДНАЯ КОРНЯ ИКС

Производная от корня равна единице, деленной на два таких же корня.

Если под корнем находится сложная функция , то производная от корня этой функции будет равна: единице, деленной на два таких же корня и умноженной на производную подкоренного выражения, то есть

Примеры вычисления производной корня

Задание. Найти производную функции

Решение. Искомая производная равна:

Согласно правилам дифференцирования , вынесем константу 2 за знак производной, в итоге будем иметь:

Ответ.

Задание. Вычислить производную функции

Решение. Искомая производная

Находим как производную сложной функции , то есть вначале находим как производную от корня, а затем умножаем на производную подкоренного выражения. В результате будем иметь:

Константу выносим за знак производной, а производная независимой переменной равна единице , тогда получаем:

Ответ.

Решить примеры вместе с преподавателем. Записывать важные информации.

Алгебра и начала математического анализа. 10-11 Алимов Москва 2014

Применение знаний и способов деятельности

Работа на доске.

Обобщение и систематизация знаний

Контроль и самоконтроль усвоения знаний и способов деятельности

Коррекция знаний и способов деятельности

Информация о домашнем задании

Записать домашнее задание

Алгебра и начала анализа

Подведение итогов занятия и рефлексия

Урок насыщенный,в доступной форме.разработка поможет детям усвоить материал.

Дата: __25-09-2018г._

Тема: Производная степенной функции.

способствовать выработке навыка вычисления производной степенной функции;

воспитывать чувство уважения между учащимися для максимального раскрытия их способностей;

воспитывать аккуратность выполнения записей в тетради и на доске;

совершенствовать умения вычислять производные.

I. Организационный момент.

II. Изучение нового материала.

Формула для вычисления производной степенной функции x n , где n — произвольное натуральное число, большее 1, такова:

Формула производной функции х 2 уже известна: (х 2 )' = 2х. Пользуясь формулой дифференцирования произведения, получаем:

(x 3 )’=( x 2 ⋅x)’= (x 2 )’x+ x 2 (x)’= 2x⋅x + x 2 ⋅1=3 x 2 ;

(x 4 )’=( x 3 ⋅x)’= (x 3 )’x+ x 3 (x)’= 3x 2 ⋅x+ x 3 ⋅1=4x 3 .

Заметим теперь, что

(x 2 )’=2x 2-1 , (x 3 )’=3x 3-1 , (x 4 )’=4x 4-1 ,т.е. для n, равного 2, 3 и 4, формула (1) доказана. Продолжая аналогичные рассуждения, нетрудно убедиться в справедливости формулы (1) для n, равного 5, 6 и т. д.

Докажем, что формула (1) верна для любого натурального n4.

Допустим, что формула (1) верна при n = k, т. е. что (x k )’=kx k-1 .

Покажем, что тогда формула (1) верна при n = k+1. Действительно,

(x k+1 )’=(x k ⋅x)’=( x k )’⋅x + x k ⋅(x)’= kx k-1 ⋅x + x k = (k+1) x k

Поэтому из того, что формула (1) верна при п = 4, следует, что она верна и при n = 5, но тогда она верна и при п = 6, а следовательно, и при n = 7 и т. д. до любого n∈ N (строгое доказательство основано на методе математической индукции).

Если n = 1 или n = 0, то при х≠0 эта формула также справедлива. Действительно, по формуле (1) при х≠0

(x 1 )’=1⋅x 1-1 = 1⋅x 0 =1,

(x 0 )’=0⋅x 0-1 = 0,что совпадает со значениями производных функций х и 1, уже известными из предыдущего пункта.

Пусть, наконец, п — целое отрицательное число, тогда n = —m, , где т — число натуральное. Применяя правило дифференцирования частного и пользуясь уже доказанной для натуральных т формулой (1), получаем при х≠0:

В результате можно сделать вывод:

Для любого целого n и любого x (x≠0 при n≤1)

Из дифференцируемости степенной функции и основных правил вычисления производных вытекает, что целые рациональные функции (многочлены) и дробно-рациональные функции дифференцируемы в каждой точке своей области определения.

III. Закрепление нового материала.

Применим правило суммы:

Вынесем постоянные множители за знак производной:

Найдем производные степенных функций:

Вычислить производную функции y=(3√)2−52√.

Производная постоянной величины равна нулю. Следовательно,

Найти производную функции y=1x+2x2+3x3.

Дифференцируем сначала как сумму функций:

Вынося постоянные множители за знак производной и вычисляя производные степенных функций, получаем

Найти производную следующей функции y=8x5−6x4+5x3−7x2+4x+3.

Используя правило дифференцирования полинома, получаем выражение для производной в виде

Найти производную функции y=x22+x33+x44.

Производная записывается в виде:

Найти производную функции y=x22−2x2.

Производная имеет следующий вид:

Вычислить значение производной функции y=x2−12x2 в точке x=1.

Производная данной функции имеет вид:

Значение производной в точке x=1 равно:

Найти производную функции y=7√3x+3√7.

Здесь мы имеем дело с линейной функцией, коэффициенты которой являются иррациональными числами. Производная будет равна

Найти производную функции y=x3−−√4.

Представив данную иррациональную функцию как степенную, получаем:

Найти производную иррациональной функции y=xn−−√m, где m≠0.

Дифференцируя как степенную функцию с дробным показателем степени, получаем

Вычислить производную функции y=x2−−√π.

Производная данной степенной функции равна

Найти производную следующей функции: y=x(x2+2)(x3−3).

Данную функцию можно представить в виде полинома:

Дифференцируя почленно, получаем:

Вычислить производную функции y=x5−−√+5x−−√.

Перепишем функцию в виде:

Используем формулу производной суммы двух функций:

Вынесем постоянные множители и вычислим производные:

Здесь мы использовали выражение (x√)′=(x12)′=12x−12=12x√. После упрощения получаем

Найти производную функции y=x√3−1x√3.

Перейдем к записи в степенной форме:

Производная разности функций, очевидно, равна разности производных этих функций:

Вычисляя производные степенных функций, получаем

Найти производную функции y=5x3+3−2x3+x5−−√3.

Преобразуем слагаемые данной функции в степенную форму:

Применяя линейные свойства производной и правило дифференцирования степенной функции, получаем:

Найти производную функции y=1x+1x√+1x√3.

Представив слагаемые в виде степенных функций, получаем следуюшее выражение для производной:

В данном видеоуроке мы вспомним определение производной функции. Познакомимся с формулой производной степенной функции.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Производная степенной функции"

Сегодня на уроке мы вспомним определение производной функции. Познакомимся с формулой производной степенной функции.

Прежде чем приступить к рассмотрению новой темы, давайте вспомним определение производной.

Итак, пусть функция определена на некотором промежутке, – точка этого промежутка и число такое, что также принадлежит данному промежутку. Тогда предел разностного отношения при (если этот предел существует), называется производной функции в точке и обозначается . Таким образом, .

Давайте с вами докажем, что .

Сейчас докажем, что .

На предыдущем занятии мы с вами получили следующие формулы для производных:

; ; ; .

На этом занятии мы доказали, что , .

Четыре последние формулы являются формулами производной степенной функции для , для , для и для .

Заметим, что эти четыре формулы мы можем записать следующим образом:

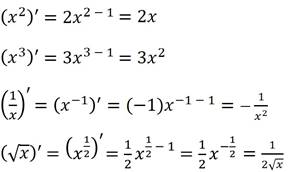
Ещё раз посмотрев на каждую из формул, сделаем вывод, что для любого действительного показателя справедлива формула производной степенной функции:

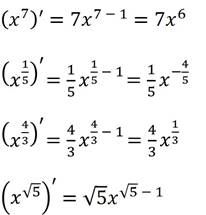
Познакомимся с ещё одной формулой. Если нам с вами надо найти производную , то мы воспользуемся формулой производной степенной функции и получим . Если надо найти , то мы воспользуемся известной вам формулой и в результате получим .

Но бывают более сложные случаи. Например, нам надо найти . Здесь мы можем воспользоваться вот такой формулой .

В нашем случае , , . Тогда по этой формуле получаем, что .

А сейчас давайте выполним несколько заданий.

Задание первое. Найдите производные функций:

а) ; б) ; в) ; г) ; д) ; е) .

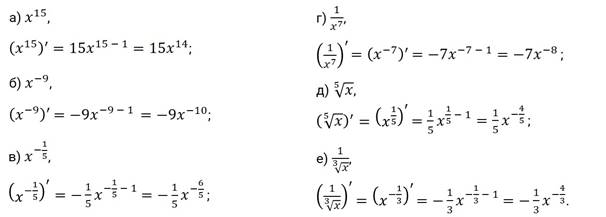
Задание второе. Найдите производные функций:

а) ; б) ; в) ; г) ; д) .

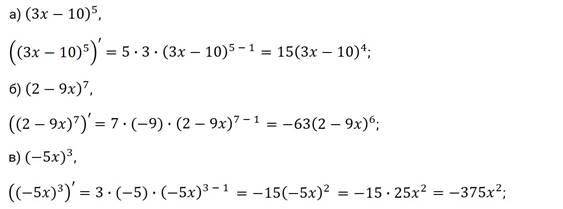
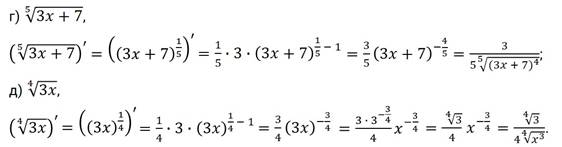
Задние третье. Найдите , если:

Данная функция является четной, значит ее график симметричен относительно оси ординат. Точки пересечения с осью абсцисс х= -1,х=1; с осью ординат у= -1. Найдем производную функции .

в точках х= -1,х=1 производная не существует.

Читайте также: