Построение графиков функций y f x b и y f x a конспект
Обновлено: 07.07.2024
Асимптота графика функции y = f(x) – прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1и х2, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Выпуклость вверх. Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка.
Выпуклость вниз. Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.
Максимум функции. Значение функции в точке максимума называют максимумом функции.
Минимум функции. Значение функции в точке минимума называют минимумом функции.
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Производная второго порядка (вторая производная). Производная второго порядка есть первая производная от производной первого порядка.
Производную определяют, как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к 0, если такой предел существует.

Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .
Точка перегиба. Точки, в которых выпуклость вверх меняется на выпуклость вниз или наоборот, называются точками перегиба.
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y=f(x) убывает на интервале X, если для любых х1 и х2 , из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.
Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит вышепроведенного отрезка.
Полная схема построения графика функции:
- Найти область определения функции D(f).
- Исследовать функцию на четность (найти f(-x)).
- Найти асимптоты.
- Найти стационарные и критические точки.
- Найти промежутки монотонности.
- Найти интервалы выпуклости вверх и выпуклости вниз.
- Найти точки перегиба
- Составить таблицу значений функции для некоторых точек.
- По полученным данным построить график функции.
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Постройте график функции у = х 3 – 3х + 3, используя краткую схему построения. схему построения.

2) Функция не является ни четной, ни нечетной, т. к.
4) f’(x) = 3x 2 – 3, f’(x) = 0 при х = 1, х = -1.
х = 1, х = -1 – стационарные точки.

5) f’(x)>0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки возрастания.

1)

2) Функция не является ни четной, ни нечетной, т. к.
3) х = 1 – вертикальная асимптота
х = 2, х = 0 – стационарные точки.

5) f’(x)>0 при . Так как в точках х = 0, х = 2 функция непрерывна, то эти точки также включаются в промежутки возрастания.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Лекция: Построение и преобразование графиков.
Преподаватель: Горячева А.О.
Графики элементарных функций
Прямая линия - график линейной функции y = ax + b . Функция y монотонно возрастает при a > 0 и убывает при a b = 0 прямая линия проходит через начало координат т. 0 ( y = ax - прямая пропорциональность)/
y =3 x +4 (построить)
Парабола - график функции квадратного трёхчлена у = ах 2 + b х + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а ax 2 + bx +с =0.
1. Найти координаты вершины параболы, выяснить направление ветвей.
2. Найти точки пересечения с осями координат.
3. Найти координаты еще 2-х контрольных точек.
у = х 2 –х – 2, у = 4х 2 +17х+1
Гипербола - график функции . При а > О расположена в I и III четвертях, при а II и IV . Асимптоты - оси координат. Ось симметрии - прямая у = х(а > 0) или у - - х(а
Дробно-линейная функция .
Функция, которую можно задать формулой вида у = , где буквой х обозначена независимая переменная, а буквами а, в, с и d – произвольные числа, причём с≠0 и аd – вс ≠ 0, называется дробно-линейной функцией.
Графиком дробно-линейной функции является гипербола.
Зная, как строить графики функции y = f(x), всегда можно построить график функции y = af(kx + b) + m.
Параллельный перенос графика вдоль оси абсцисс на | b | единиц:
влево, если b > 0;
Параллельный перенос графика вдоль оси ординат на | m | единиц:
вверх, если m > 0,
Симметричное отражение графика относительно оси ординат.
Симметричное отражение графика относительно оси абсцисс.
Сжатие и растяжение графика
При k > 1 — сжатие графика к оси ординат в k раз, при 0
При k > 1 — растяжение графика от оси абсцисс в k раз, при 0
Преобразования графика с модулем
При f(x) > 0 — график остаётся без изменений, при f(x)
При x>0 — график остаётся без изменений, при x
Cуществует 2 алгоритма построения графика функции вида у =f(х+t)+m,
Алгоритм 1:
Построить график функции у =f(x).
Осуществить параллельный перенос графика у =f(x) вдоль оси х на |t| масштабных единиц влево, если t>0, и если t
Осуществить параллельный перенос полученного на втором шаге графика вдоль оси у на |m| масштабных единиц вверх, если m>0, и вниз, если m
Алгоритм 2:
Перейти к вспомогательной системе координат, проведя (пунктиром) вспомогательные прямые х =-t, у = m, т.е. выбрав в качестве начала новой системы координат точку(-t;m).
К новой системе координат "привязать" график функции у =f(х).
Пример 1 . Построим график функции у =(х+3) 2 +1
Введем вспомогательную систему координат: это прямые х=-3, у=1. Основная функция у=х 2
График функции у =(х+3) 2 +1 получается с помощью сдвига функции у=х 2 на 3 масштабные единицы влево и на 1 единицу вверх.
Задачи урока: 1. Экспериментальным путём вывести алгоритм построения графиков функций у=f(x)+b и у=f(x+a). 2. Развивать у обучающихся умения сравнивать, анализировать и обобщать изучаемые факты.
Если вам понравилась статья, лучший способ сказать cпасибо — это поделиться ссылкой со своими друзьями в социальных сетях :)
Также вас может заинтересовать



Войти на сайт
Войти через социальную сеть
Свидетельство участника образовательного сообщества
Скачайте документ бесплатно сразу после регистрации на сайте.

Презентация содержит в себе все этапы урока и может быть использована на нем без привлечения дополнительных источников.


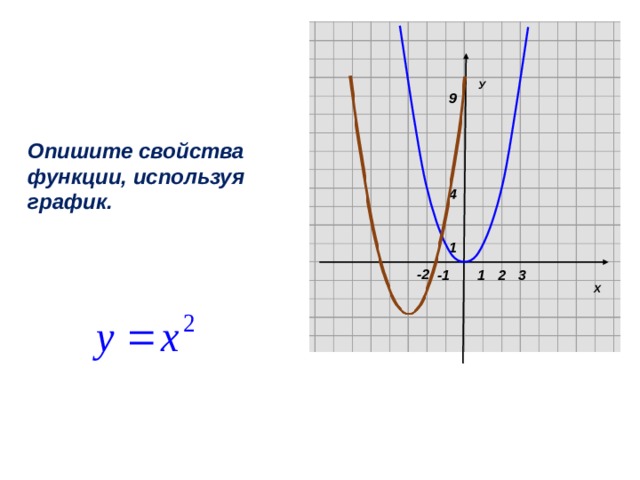
Опишите свойства
функции, используя
график.

Урок повторения
Сдвиг графика функции вдоль осей координат

Цели :
График квадратичной функции вида
у=ах 2
0 ,5
4 ,5
0 ,5
4 ,5
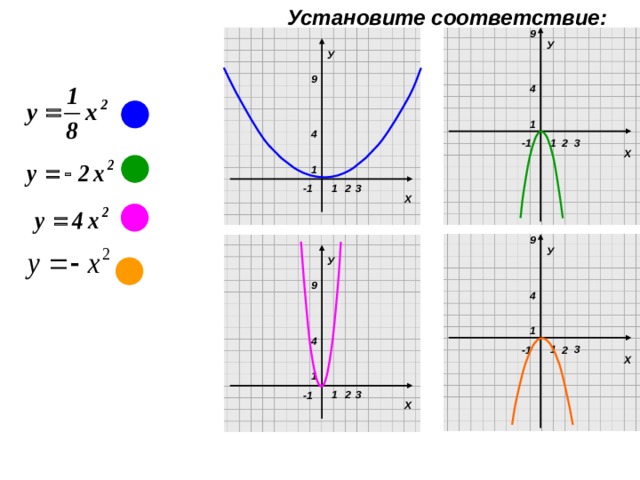
Установите соответствие :
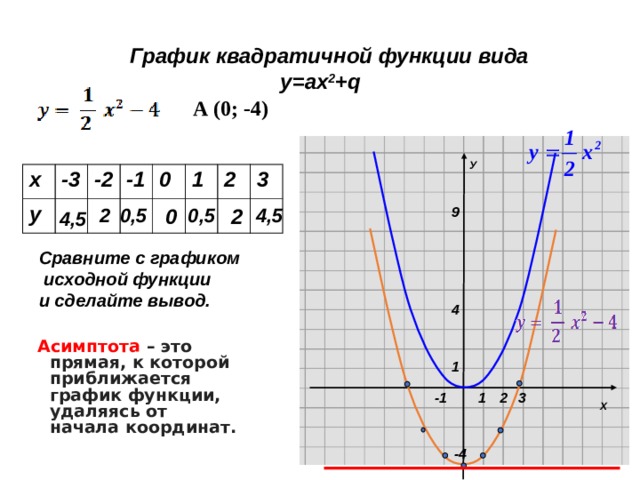
Асимптота – это прямая, к которой приближается график функции, удаляясь от начала координат.
Читайте также:

