Переход к новому основанию конспект

Обновлено: 07.07.2024

Цели: вывести формулу перехода к новому основанию логарифма и сформировать представление о связи логарифмических функций с разными основаниями логарифма; вывести два следствия из указанной формулы; формировать умение использовать формулу перехода для решения задач.

I. Организационный момент.

II. Устная работа.

а) log 2 16; б) 32; в) lg 0,0001;

г) log 3 + log 2 18; д) lg 500 – lg 5; е) log 5 25 4 .

2. Замените * соответствующим числом.

а) log * 4 = –2; б) = 11; в) log 2 16 * = 20;

г) log 2 100 – log 2 * = 1; д) = 81; е) = 1.

III. Объяснение нового материала.

1. Актуализация знаний.

Вспоминаем, как связаны графики функций y = f ( x ), y = f ( x ) + b ,
y = k · f ( x ), y = f ( x + a ) и y = f ( mx ). Механические преобразования предполагают параллельный перенос либо сжатие (растяжение) вдоль осей координат графика исходной функции.

2. На рисунке 215 учебника представлены графики функций y = log 2 x , y = log 3 x . Замечаем, что график функции y = log 2 x получен растяжением графика функции y = log 3 x вдоль оси Oу . Но возможно это только видимость, доказать можно вывод, если верно равенство log 2 x = k · log 3 x , где k – некоторое число. Возникает проблемная ситуация.

3. Для решения поставленной проблемы нам необходима теорема:

log a b = , где a > 0, b > 0, c > 0, a ≠ 1.

Пусть x = log a b , y = log c b , z = log c a , тогда a x = b ; c y = b ; c z = a , значит, a x = c y . Так как a = c z , то ( c z ) x = c y , то есть c zx = c y . Следовательно, zx = y , то есть x = или log a b =

Необходимо провести это доказательство с учащимися в классе. Это позволит еще раз проследить связь взаимообратных функций y = log a x и y = a x .

4. На основании доказанной теоремы мы можем подтвердить свою догадку:

log 3 x = ⇒ log 2 x = log 2 3 · log 3 x .

Значит, коэффициент растяжения k = log 2 3.

5. Предлагаем учащимся самостоятельно вывести следствия из доказанной теоремы. На доску выносим запись всех трех формул.

Третью формулу можно также выписать в виде:

IV. Формирование умений и навыков.

1. Упражнения, выполняемые на этом уроке, направлены как на закрепление самой формулы перехода к новому основанию логарифма, так и на применение её и её следствий для вычисления значений выражений и сравнения чисел. В каждом примере возникает необходимость обоснования выбора нового основания логарифма, к которому осуществляется переход.

2. № 46.1 (а; б), № 46.2, № 46.4 (а; б)

а) log 2 + log 4 9 = log 2 + 3 2 = log 2 + log 2 3 =
= log 2 = log 2 1 = 0.

б) log 3 = log 3 2 –1 = –1 · log 3 2 = –1 · ;

в) log 3 4 = log 3 2 2 = 2 log 3 2 = 2 · ;

г) log 3 = log 3 4 –1 = – log 3 4 = .

а) log 4 9 = 3 2 = log 2 3 = a ;

б) log 8 18 = log 8 2 + log 8 9 = 2 + 3 2 = log 2 2 +
+ · 2 · log 2 3 = a = ;

в) log 4 81 = log 4 9 2 = 2 log 4 9 = 2 a ;

г) log 8 54 = log 8 (18 · 3) = log 8 18 + log 8 3 = + 3 =
= + · log 2 3 = = a + .

3. № 46.5 (а; б), № 46.6 (а; б).

Для сравнения чисел необходимо привести логарифмы к одному основанию. Кроме того, необходимо учитывать характер монотонности логарифмической функции.

log 2 7 и log 7 4.

Приведем второй логарифм к основанию 2.

log 7 4 = 2 log 7 2 = .

Оценим полученные выражения:

Значит, 2 7, или log 7 4 2 7.

Функция y = x – монотонно убывает. Так как 3 > , то 3 , значит, 3 1,5.

4. № 46.9 (а; б), № 46.10*.

Для решения упражнений данной группы учащимся необходимо применять все ранее изученные свойства логарифмов и формулу перехода к новому основанию логарифма.

Необходимо побуждать ребят использовать разные следствия теорем о переходе к новому основанию в зависимости от задачной ситуации.

б) log 3 8 · log 2 27 – = log 3 2 3 · log 2 3 3 – =
= 3 · log 3 2 · 3 · log 2 3 – = 9 – 5 = 4.

а) = log 2 56 · log 2 28 – log 2 7 · log 2 224 =
= (log 2 7 + log 2 8)(log 2 4 + log 2 7) – log 2 7 (log 2 7 + log 2 32) =
= (log 2 7 + 3)(2 + log 2 7) – log 2 7 (log 2 7 + 5) = 2 log 2 7 + +
+ 6 + 3 log 2 7 – – 5 log 2 7 = 6.

б) = log 3 135 · log 3 45 – log 3 5 · log 3 1215 =
= (log 3 5 + log 3 27)(log 3 5 + log 3 9) – log 3 5 (log 3 5 + log 3 243) =
= (log 3 5 + 3)(log 3 5 + 2) – log 3 5 (log 3 5 + 5) = + 2 log 3 5 +
+ 3 log 3 5 + 6 – – 5 log 3 5 = 6.

– Каким образом связаны графики различных логарифмических функций?

– Назовите формулу перехода к новому основанию логарифма.

– Какие следствия существуют из теоремы о переходе к новому основанию логарифма?

Домашнее задание: № 46.1 (в; г), № 46.3, № 46.4 (в; г), № 46.5 (в; г), № 46.6 (в; г), № 46.9 (в; г).

По теме: методические разработки, презентации и конспекты

План – конспект урока алгебры и начала анализа в 11 классе по теме "Применения производной".

План -конспект урока алгебры в 11 классе.

конспект урока, алгебра и начала анализа, 10 класс, Применение производной

Конспект урока по алгебре и началам анализа к учебнику Колмагорова 10 класс по теме Применение производной.

Планы конспекты уроков алгебра и начала анализа 10 класс.

Архив содержит планы конспекты уроков алгебра и начала анализа 10 класс по учебнику Мордковича. Понятие производной, нахождение производной. Самостоятельные работы по данным темам.

Конспект урока алгебры и начал анализа в 11 классе по теме "Иррациональные уравнения"

Урок по формированию у учащихся умений решать иррациональные уравнения.

Конспект урока алгебры и начала анализа для 10 класса "Понятие логарифма"

Урок направлен на формирование понятия логарифма, изучение его основных свойств и развитие умения применять эти свойства при решении заданий.

На этом уроке вводится формула перехода к новому основанию логарифма. Вводятся свойства логарифмов, которые следуют из этой формулы.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Переход к новому основанию логарифма"

• ввести формулу перехода к новому основанию логарифма;

• познакомить со свойствами логарифмов, которые следуют из этой формулы.

Прежде чем перейти к изучению нового материала, давайте повторим некоторый теоретический материал.

Решая логарифмические уравнения и неравенства у нас встречались логарифмы, основания которых либо были одинаковыми, либо приводились к одинаковым путем простейших преобразований. А как же быть, если в уравнении или неравенстве присутствуют логарифмы, основания которых нельзя путем простейших преобразований привести к одинаковому числу?

Например, можно ли как-нибудь преобразовать:

И если да, то какое основание будет у такого логарифма и какой будет подлогарифмическая функция?

Для решения такого рода заданий используется следующая теорема:

Эта формула называется формулой перехода к новому основанию логарифма.

Докажем эту формулу.

Теперь можно очень просто логарифм по основанию 2 преобразовать в логарифм с основанием 3.

Таким образом, мы получили, что:

То есть логарифмы одной функции, но разных оснований отличаются в k раз.

Аналогично, можно записать, что:

Это равенство выполняется для логарифмов по произвольному основанию.

Рассмотрим частные случаи данной формулы.

Следствие 1.

Доказательство.

Следствие 2.

Доказательство.

Рассмотрим пример.

Рассмотрим еще один пример.

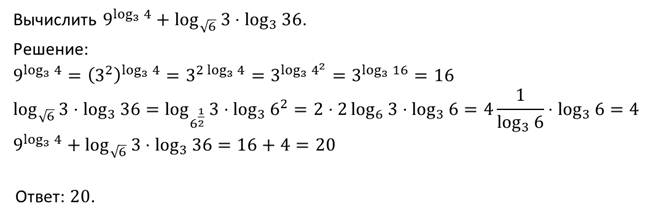
Давайте еще раз повторим формулы, с которыми мы познакомились на этом уроке:

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Переход к новому основанию..doc

Технологическая карта (план) занятия №14

Предмет

Тема занятия

Переход к новому основанию.

Вид занятия

(тип урока )

Комбинированный

Время

Цель занятия

Учебная: повторить определение логарифма числа, основное логарифмическое тождество;

закрепить основные свойства логарифмов;

познакомить обучающихся с формулой перехода к новому основанию, научиться применять ее при решении задач.

Воспитательная: воспитывать внимательность при записи лекций, аккуратность, самостоятельность.

Развивающая: развивать математические способности, логическое мышление, навыки самоконтроля.

Компетенции:

общие:

профессиональные

Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности (ОК 2)

Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами (ОК 4)

Осуществлять устную и письменную коммуникацию на государственном языке с учетом особенностей социального и культурного контекста (ОК 5)

Обеспечение занятия

Наглядные пособия: мультимедийная презентация;

Технические средства обучения: ноутбук, проектор;

Учебные места (для лаб. работ, прак. занятий): 204 аудитория;

Д. Литература: 1) Математика: алгебра и начала математического анализа, геометрия: учеб. для студ. учреждений сред. проф. образования/ М.И.Башмаков.

2) Ш.А. Алимов и др. Алгебра и начала анализа, 10-11 кл.

3) А.Г. Мордкович и др. Алгебра и начала анализа, 10-11 кл. Задачник.

Содержание занятия

I 1. .1

2 Орг. момент.

-проверка присутствующих на занятии;

-проверка готовности учащихся к занятию;

-формулировка целей занятия.

Проверка домашнего задания н

1. Сформулировать определение логарифма числа в по основанию а.

2. Записать на доске основное логарифмическое тождество.

3.Сформулировать определение десятичных логарифмов.

4. Сформулировать определение натуральных логарифмов.

5. Соотнести свойства логарифмов на слайде.

6. Устная работа на слайде.

Изучение нового материала

Формула перехода от одного основания логарифма к другому используется для решения уравнений. Пусть мы хотим перейти от логарифмов по основанию а к логарифмам по другому основанию c . Запишем основное логарифмическое тождество: a = b

Прологарифмируем его по основанию c : log = log , используя свойство логарифма получим: log * log = log , отсюда получим ,

Где b >0, a >0, a ≠1, c >0, c ≠1

Следствия: ей ,

Пример1: Пример 2: (из учебника на стр 96.)

формацией выполняет аз

Решение упражнений. № 305, № 306, № 308, № 314

1597 . ( Задачник МордковичА . Г .)

Известно, что log ₂3= a . Найдите:

*** Дано : lg3=a, lg5=b. Вычислить : log ₂ 15.

Решение : log ₂ 15= (lg15/ lg2)= lg(3*5)/ lg(10/5)= (lg3+ lg5)/ (lg10- lg5)=(a+b)/(1-b)

Итог занятия.

Задание на дом: конспект лекций ; № 309, №310, стр.97 .; № 1598 у (Задачник МордковичА.Г.)

На этом уроке мы познакомимся с важнейшим свойством логарифмов, которое называется свойством перевода логарифма к новому основанию. Из этого свойства мы выведем несколько следствий. Также мы рассмотрим примеры, при решении которых используются формула перехода к новому основанию и следствия из нее.

I. Организационный момент.

II. Устная работа.

а) log ₂ 16; б) 32; в) lg 0,0001;

г) log ₃ + log ₂ 18; д) lg 500 – lg 5; е) log ₅ 25 4 .

2. Замените * соответствующим числом.

а) log _* 4 = –2; б) = 11; в) log ₂ 16 * = 20;

г) log ₂ 100 – log ₂ * = 1; д) = 81; е) = 1.

III. Объяснение нового материала.

1. Актуализация знаний.

Вспоминаем, как связаны графики функций y = f (x), y = f (x) + b,
y = k · f (x), y = f (x + a) и y = f (mx). Механические преобразования предполагают параллельный перенос либо сжатие (растяжение) вдоль осей координат графика исходной функции.

2. На рисунке 215 учебника представлены графики функций y = log ₂ x, y = log ₃ x. Замечаем, что график функции y = log ₂ x получен растяжением графика функции y = log ₃ x вдоль оси Oу. Но возможно это только видимость, доказать можно вывод, если верно равенство log ₂ x = k · log ₃ x, где k – некоторое число. Возникает проблемная ситуация.

3. Для решения поставленной проблемы нам необходима теорема:

log _a b = , где a 0, b 0, c 0, a  1.

 Пусть x = log _a b, y = log _c b, z = log _c a, тогда a x = b; c y = b; c z = a, значит, a x = c y . Так как a = c z , то (c z ) x = c y , то есть c zx = c y . Следовательно, zx = y, то есть x = или log _a b = 

Необходимо провести это доказательство с учащимися в классе. Это позволит еще раз проследить связь взаимообратных функций y = log _a x и y = a x .

4. На основании доказанной теоремы мы можем подтвердить свою догадку:

log ₃ x =  log ₂ x = log ₂ 3 · log ₃ x.

Значит, коэффициент растяжения k = log ₂ 3.

Третью формулу можно также выписать в виде:

IV. Формирование умений и навыков.

2. № 46.1 (а; б), № 46.2, № 46.4 (а; б)

а) log ₂ + log ₄ 9 = log ₂ + 3 2 = log ₂ + log ₂ 3 =
= log ₂ = log ₂ 1 = 0.

б)

= 2.

а) log ₃ 2 = ;

б) log ₃ = log ₃ 2 –1 = –1 · log ₃ 2 = –1 · ;

в) log ₃ 4 = log ₃ 2 2 = 2 log ₃ 2 = 2 · ;

г) log ₃ = log ₃ 4 –1 = – log ₃ 4 = .

а) log ₄ 9 = 3 2 = log ₂ 3 = a;

б) log ₈ 18 = log ₈ 2 + log ₈ 9 = 2 + 3 2 = log ₂ 2 +
+ · 2 · log ₂ 3 = a = ;

в) log ₄ 81 = log ₄ 9 2 = 2 log ₄ 9 = 2a;

г) log ₈ 54 = log ₈ (18 · 3) = log ₈ 18 + log ₈ 3 = + 3 =
= + · log ₂ 3 = = a + .

3. № 46.5 (а; б), № 46.6 (а; б).

Приведем второй логарифм к основанию 2.

log ₇ 4 = 2 log ₇ 2 = .

Оценим полученные выражения:

;

Значит, ₂ 7, или log ₇ 4 ₂ 7.

3 и 1,5.

Имеем: .

Функция y = x – монотонно убывает. Так как 3 , то 3 , значит, 3 1,5.

4. № 46.9 (а; б), № 46.10*.

а)
+ = 16 + 4 = 20;

б) log ₃ 8 · log ₂ 27 – = log ₃ 2 3 · log ₂ 3 3 – =
= 3 · log ₃ 2 · 3 · log ₂ 3 – = 9 – 5 = 4.

а) = log ₂ 56 · log ₂ 28 – log ₂ 7 · log ₂ 224 =
= (log ₂ 7 + log ₂ 8)(log ₂ 4 + log ₂ 7) – log ₂ 7 (log ₂ 7 + log ₂ 32) =
= (log ₂ 7 + 3)(2 + log ₂ 7) – log ₂ 7 (log ₂ 7 + 5) = 2 log ₂ 7 + +
+ 6 + 3 log ₂ 7 – – 5 log ₂ 7 = 6.

б) = log ₃ 135 · log ₃ 45 – log ₃ 5 · log ₃ 1215 =
= (log ₃ 5 + log ₃ 27)(log ₃ 5 + log ₃ 9) – log ₃ 5 (log ₃ 5 + log ₃ 243) =
= (log ₃ 5 + 3)(log ₃ 5 + 2) – log ₃ 5 (log ₃ 5 + 5) = + 2 log ₃ 5 +
+ 3 log ₃ 5 + 6 – – 5 log ₃ 5 = 6.

V. Итоги урока.

– Каким образом связаны графики различных логарифмических функций?

– Назовите формулу перехода к новому основанию логарифма.

– Какие следствия существуют из теоремы о переходе к новому основанию логарифма?

Домашнее задание: № 46.1 (в; г), № 46.3, № 46.4 (в; г), № 46.5 (в; г), № 46.6 (в; г), № 46.9 (в; г).

Читайте также: