Конспект урока компланарные векторы 11 класс атанасян
Обновлено: 05.07.2024
Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскости.
векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
На рисунке векторы CA,CA1,DD1 компланарны, так как, если отложить от точки C вектор CC1=DD1 то все три вектора CA, CA1,CC1 и окажутся лежащими в одной плоскости. Векторы DC,CA,DD1 не компланарны, так как вектор DD1 не лежит в плоскости ACD.
Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также компланарны. Три произвольных вектора могут быть как компланарными, так и некомпланарными.
Докажем признак компланарности трех векторов. Если вектор можно представить в виде =x , где х и у – некоторые числа, то векторы – компланарны.
Для доказательства будем считать, что векторы а и в неколлинеарны, так как если они коллинеарны, то компланарность очевидна. Отложим от произвольной точки О векторы ОА и ОВ, равные соответственно векторам данным а и в. Вектороы ОА и ОВ лежат в одной плоскости ОАВ. Вектор ОА1 равен вектору ОА, умноженному на число х. Вектор ОВ1 равен вектору ОВ, умноженному на число у. Векторы ОА1 и ОВ1 так же лежат в этой плоскости. Следовательно, их сумма тоже лежит в этой плоскости. А их сумма равна вектору с. Значит , и вектор с лежит в этой плоскости. Векторы а, в и с компланарны. Что и требовалось доказать.
Справедливо и утверждение, обратное признаку компланарности векторов:
Если векторы а, в, с компланарны, а векторы а и в неколлинеарны, то вектор с можно представить как сумму x , при чем коэффициенты х и у определяются единственным образом.
В таком случае говорят, что вектор с разложен по векторам а и в.
Рассмотрим задачу №355(а) Дан параллелепипед АВСDA1B1C1D1.
Компланарны ли векторы АА1, СС1, ВВ1?
Решение : Три вектора, среди которых имеются два коллинеарных, компланарны. А в нашем случае все три вектора являются коллинеарными так как лежат на параллельных ребрах параллелепипеда, значит, эти векторы компланарны.
Дан параллелепипед АВСDA1B1C1D1.
Компланарны ли векторы АD, СС1, А1В1?
Решение: Вектор АА1 равен вектору СС1, вектор АВ равен А1В1. Векторы АВ, АD и АА1 не компланарны, так как вектор АА1 не лежит в плоскости АВС. Значит, и АD, СС1, А1В1- некомпланарны.
по ОУДу,04 Математика: алгебра и начала анализа, геометрия.
учебной дисциплине/междисциплинарному курсу
для обучающихся гр. 101, 103, 106, 108, 112, курс 1,
специальность 40.02.01. ПРАВО И ОРГАНИЗАЦИЯ СОЦИАЛЬНОГО ОБЕСПЕЧЕНИЯ
дата проведения 7 мая 2018 г.
преподаватель Л.В. Лазарева
Обучающая : обучение решению задач на разложения вектора по трем некомпланарным направлениям.
Воспитательная: воспитание внимательности, аккуратности.
Развивающая: развитие пространственного воображения, умения самостоятельной работы с учебной литературой, с электронными носителями.
- И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
- Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
- Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Webmath.exponenta.ru ( Источник ).
- СтудопедиЯ ( Источник ).
- Научная библиотека ( Источник ).
Междисциплинарные связи: алгебра и начала анализа, информатика, естествознание.
Внутридисциплинарные связи: раздел 3, геометрия: параллелограмм, свойства параллелограмма, геометрические преобразования пространства, метод координат.
1.АКТУАЛИЗАЦИЯ РАНЕЕ ИЗУЧЕННОГО МАТЕРИАЛА УЧЕБНОГО КУРСА
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
(по 5-ти бальной шкале)
- Справедливы ли утверждения: а) любые два противоположно направленных вектора коллинеарны; б)любые два коллинеарных вектора сонаправлены; в)любые два равных вектора коллинеарны; г)любые два сонаправленных вектора равны.
- Приведите примеры векторов, известных вам из физики.
- Обозначьте векторы с началами А и В и концами С и D соответственно.
2.ИЗУЧАЕМЫЕ ВОПРОСЫ УЧЕБНОГО ЗАНЯТИЯ
1.Основные определения по теме векторы.
2.Разложение вектора на плоскости и в пространстве.
3.Решение задач на разложение вектора по трем некомпланарным направлениям.
Вектором называется направленный отрезок. У вектора точка А – начало вектора, точка В – конец.
Для вектора важна не только длина, но и направление.
Коллинеарными называют векторы, лежащие на одной прямой или на параллельных прямых.
Коллинеарные векторы могут быть сонаправленными и противоположно направленными.
Равными называют коллинеарные сонаправленные векторы, длины которых равны.
Любой вектор можно единственным образом отложить от произвольной точки.
Для сложения векторов применяются правила треугольника, параллелограмма, многоугольника и параллелепипеда.
При умножении вектора на положительное число его длина умножается на это число, а направление остается неизменным. При умножении вектора на отрицательное число его длина умножается на это число, а направление меняется на противоположное.
Новым для векторов в пространстве относительно векторов на плоскости является понятие компланарности.
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
Источники дополнительной информации по 1 вопросу
Автор и наименование
(форма доступа для Интернет-ресурсов)
2..И Ф. Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
3..Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
Контрольные задания по вопросу 1.
(по 5-ти бальной шкале)
- Выполните рисунок параллелепипеда и выделите цветом равные векторы.
Мы знаем, что если заданы два неколлинеарных вектора на плоскости, то любой третий вектор на той же плоскости можно однозначно разложить по этим векторам (рис. 1, 2):
Рис. 1. Векторы на плоскости
Рис. 2. Разложение вектора через два неколлинеарных
Данный факт легко доказывается. Пусть . Из точки С проводим прямую CB, параллельно вектору . Получаем вектор , коллинеарный вектору . Аналогично из точки С проводим прямую CА, параллельно вектору . Получаем вектор , коллинеарный вектору . Это означает, что существуют такие два числа х и у, причем единственные, что:
Вопрос на понимание компланарности векторов. Если вектор можно представить в виде , где х и у – конкретные числа, то векторы и компланарны.
Если заданы три некомпланарных вектора, то мы можем однозначно разложить любой заданный четвертый вектор через три заданных. Например, заданы некомпланарные векторы и .Тогда любой вектор можно представить в виде суммы: , где х, у и z – конкретные числа, причем для заданного вектора единственные. Эти числа называются коэффициентами разложения.
Источники дополнительной информации по 2 вопросу
Автор и наименование
(форма доступа для Интернет-ресурсов)
2. И. Ф. Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / И. Ф. Шарыгин – М.: Дрофа, 1999. – 208 с.: ил.
3. Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
Контрольные задания по вопросу 2.
(по 5-ти бальной шкале)
- Запишите формулу для разложения вектора в пространстве по трем некомпланарным направлениям.
2. №355, стр.95, (Л. С. Атанасян)
3.№359 (а), стр.95, (Л. С. Атанасян)
Задача 1: дан куб с ребром m. Точка К – середина ребра . Разложить вектор по векторам и найти его длину.
Решение: построим заданный куб (рис. 3).
Рис. 3. Куб, задача 1
Векторами и задается плоскость квадрата . Третий вектор не лежит в этой плоскости, отсюда заключаем, что три заданных вектора , и некомпланарны, и мы можем выразить через них искомый вектор . Найдем вектор по правилу многоугольника. Очевидно, что в данной задаче для этого есть множество способов, но мы выбираем самый короткий путь: . вектор мы по условию обозначили как вектор . Вектор согласно свойствам куба равен вектору , обозначенному за вектор .
вектор составляет половину вектора , так как точка К – середина ребра по условию: . Вектор согласно свойствам куба, равен вектору , обозначенному как вектор . Имеем:
Так, заданный вектор выражен через три некомпланарных вектора. Осталось найти его длину. Здесь нужно применить теорему Пифагора. Рассмотрим прямоугольный треугольник . Он прямоугольный потому, что ребро перпендикулярно всей плоскости основания , значит и любой прямой в этой плоскости, значит прямой . Один из катетов равен m как ребро куба. Катет найдем из другого прямоугольного треугольника – , где он уже является гипотенузой. Здесь катет равен m как ребро куба. Катет равен , так как точка К – середина ребра . Имеем:
Вернемся к первому треугольнику:
Задача 2 : векторы , и компланарны. Компланарны ли векторы , и ? Компланарны ли векторы ?
Решение: тот факт, что векторы , и компланарны, означает, что, будучи отложенными от одной точки, они расположены в одной плоскости (рисунок 4.а). Это значит, что один из векторов, например, вектор , можно однозначно разложить по двум другим: . Очевидно, что векторы , и тоже компланарны, т. к. умножение вектора на положительное число не меняет его направления, а меняет только длину, и векторы останутся в той же плоскости (рисунок 4.б).
Очевидно, что тройка векторов также компланарна, потому что всякая линейная комбинация компланарных векторов есть вектор, им компланарный. Мы имеем три вектора, компланарных заданным векторам, очевидно, что они компланарны между собой.
Итак, мы вспомнили все основные определения и теоремы касательно векторов в пространстве, подробно остановились на понятии компланарности векторов и рассмотрели типовые задачи на эту тему.
Источники дополнительной информации по 3 вопросу
Автор и наименование
(форма доступа для Интернет-ресурсов)
1.И. Ф. Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / И. Ф. Шарыгин – М.: Дрофа, 1999. – 208 с.: ил.
2.Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
- признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов.
- основы векторного метода решения задач.
Основная литература:
Атанасян Л.С. и др. Геометрия. Учебник для 10-11классов - М.: Просвещение, 2017. C. 77-85.
Теоретический материал для самостоятельного изучения:
Противоположно направлены и их длины равны.
Сонаправлены и их длины равны.
Лежат на одной или параллельных прямых
Появилось новое понятие о векторах в пространстве, которого не было на плоскости - компланарность векторов. С определения компланарных векторов и начинаются главные отличия векторов в планиметрии и стереометрии.
Компланарные векторы.
Определение2.Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Рассмотрим некоторые случаи:
1 случай. Любые два вектора всегда будут компланарными, ведь через них
можно провести прямые, а через две прямые всегда можно провести
единственную плоскость.
2 случай. Три вектора будут компланарными если среди них есть пара коллинеарных
векторов. Тогда через один из коллинеарных векторов и вектор не коллинеарный ему
можно провести плоскость. А для второго из коллинеарных векторов легко
изобразить равный в этой плоскости.
3 случай. Если хотя бы один из трёх векторов является нулевым, то эти три вектора компланарны
Из планиметрии: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Следующая теорема выражает признак компланарности трех векторов. Теорема (признак) Если вектор можно представить в виде = х + у, где х и у - некоторые числа, то векторы , и компланарны.
Для сложения трёх некомпланарных векторов можно пользоваться правилом параллелепипеда. Отложим от произвольной точки О векторы =, =, = и построим параллелепипед так, чтобы отрезки ОА, ОВ и ОС были рёбрами.
Тогда ОD - диагональ этого параллелепипеда равна сумме векторов, и . Если вектор можно представить в виде суммы: = х + у + z, то говорят, что вектор d разложен по векторам , и . Числа х, у, z называют коэффициентами разложения.
Теорема. Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.
Часть 2. Векторный метод решения задач
Векторный метод решения задач – один из наиболее общих методов решения геометрических задач. Векторное решение стереометрических задач значительно проще их решения средствами элементарной геометрии.
Рассмотрим следующую задачу: Доказать, что прямая, проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон.
Пусть ABCD - данная трапеция, M и N - середины оснований BC И AD, а O - точка пересечения прямых AB и CD.
Докажем, что точка О лежит на прямой МN.
Решением задач векторным методом занимались ученые: Уильман Гамильтон Иога́нн Берну́лли, Пьер Ферма, Рене Декарт, Леонард Эйлер.
Примеры и разбор решения заданий тренировочного модуля:
Задача. В параллелепипеде АВСDА1В1С1D1 М —точка пересечения диагоналей грани A1B1C1D1, точка K — середина ребра ВВ1. Докажите, что прямые А1В1, KМ и ВС1 параллельны некоторой плоскости.
Решение. Введем векторы: . Векторы некомпланарны.
Разложим векторы и по векторам. Получим:
+= .
Тогда векторы = + компланарны. Следовательно, они параллельны некоторой плоскости, тогда этой плоскости параллельны и прямые А1В1, KМ и ВС1.

Рисунки Савченко Е.М. Рисунки в презентации выполнены с помощью инструментов панели рисования программы Microsoft PowerPoint .
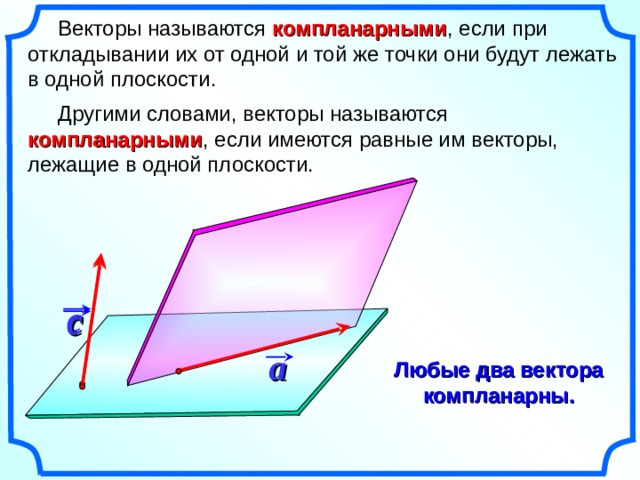
Векторы называются компланарными , если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
Другими словами, векторы называются компланарными , если имеются равные им векторы, лежащие в одной плоскости.
Любые два вектора компланарны.
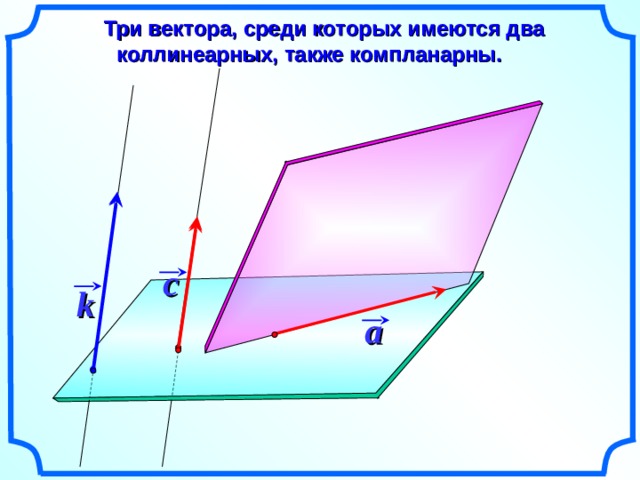
Три вектора, среди которых имеются два коллинеарных, также компланарны.
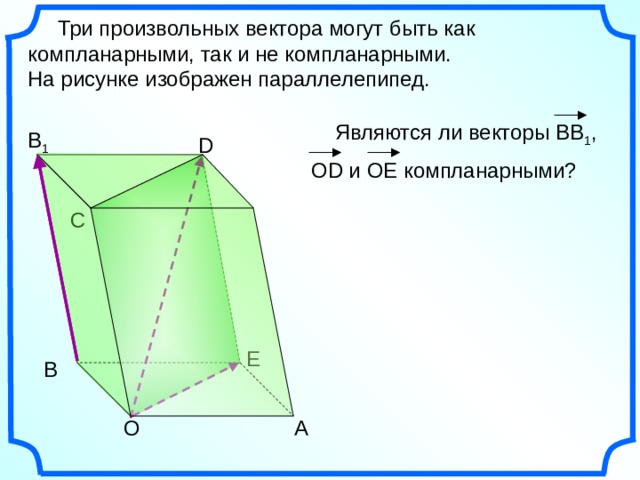
Три произвольных вектора могут быть как компланарными, так и не компланарными.
На рисунке изображен параллелепипед.
Являются ли векторы ВВ 1 ,
О D и ОЕ компланарными?
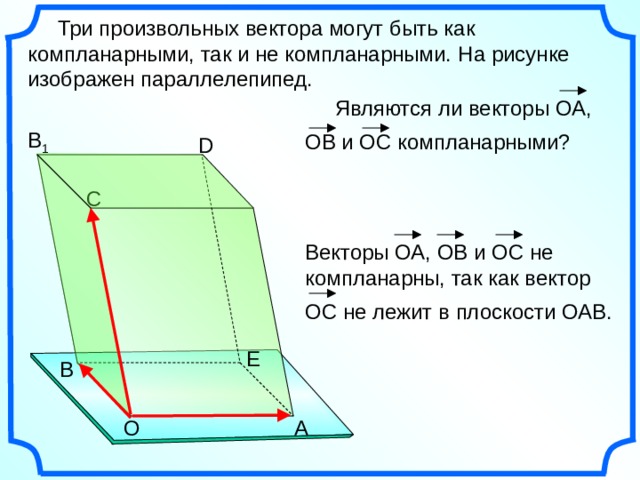
Три произвольных вектора могут быть как компланарными, так и не компланарными. На рисунке изображен параллелепипед.
Являются ли векторы ОА,
ОВ и ОС компланарными?
Векторы ОА, ОВ и ОС не компланарны, так как вектор
ОС не лежит в плоскости ОАВ.
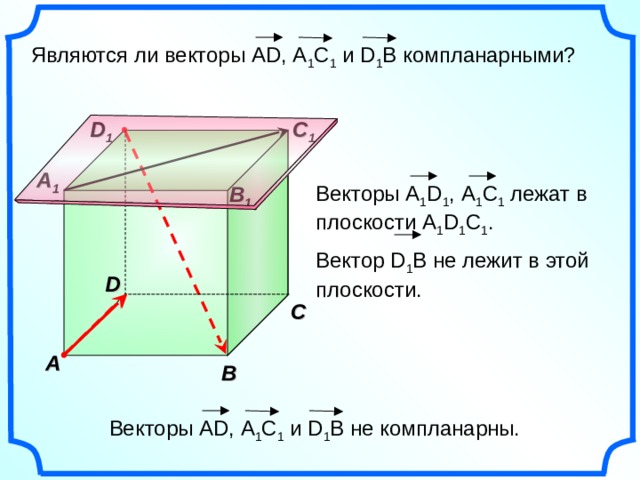
Являются ли векторы AD , А 1 С 1 и D 1 B компланарными?
D 1
C 1
A 1
Векторы А 1 D 1 , A 1 C 1 лежат в плоскости А 1 D 1 C 1 .
Вектор D 1 В не лежит в этой плоскости.
B 1
Векторы AD , А 1 С 1 и D 1 B не компланарны.
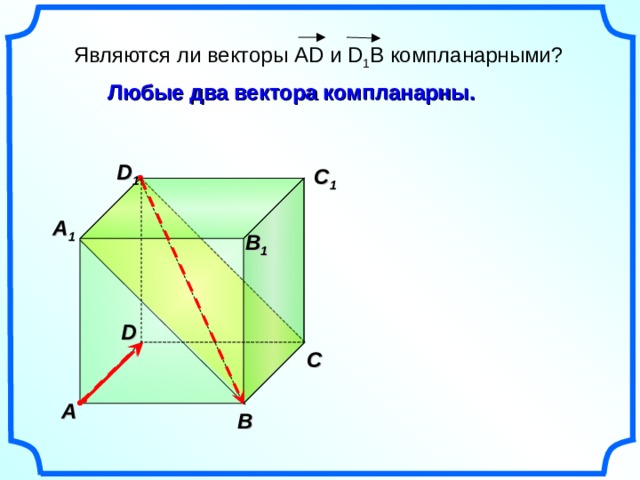
Являются ли векторы AD и D 1 B компланарными?
Любые два вектора компланарны.
D 1
C 1
A 1
B 1
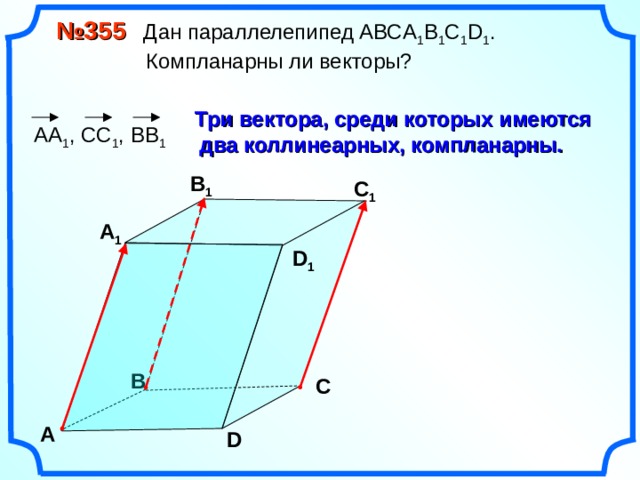
№ 355 Дан параллелепипед АВС A 1 B 1 C 1 D 1 .
Компланарны ли векторы?
Три вектора, среди которых имеются
два коллинеарных, компланарны.
АА 1 , СС 1 , ВВ 1
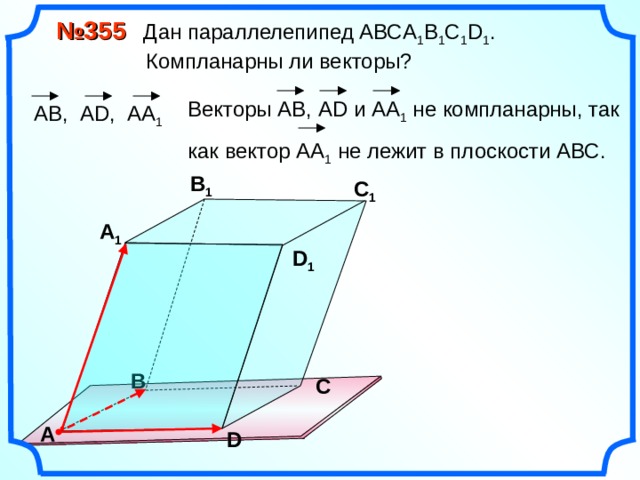
№ 355 Дан параллелепипед АВС A 1 B 1 C 1 D 1 .
Компланарны ли векторы?
Векторы АВ, А D и АА 1 не компланарны, так
как вектор АА 1 не лежит в плоскости АВС.
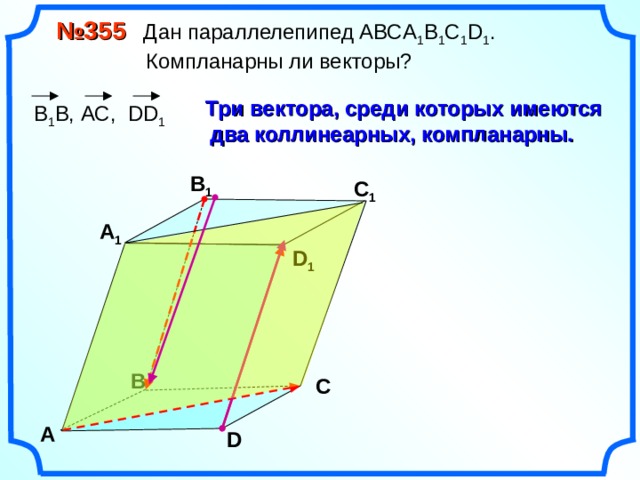
№ 355 Дан параллелепипед АВС A 1 B 1 C 1 D 1 .
Компланарны ли векторы?
Три вектора, среди которых имеются
два коллинеарных, компланарны.
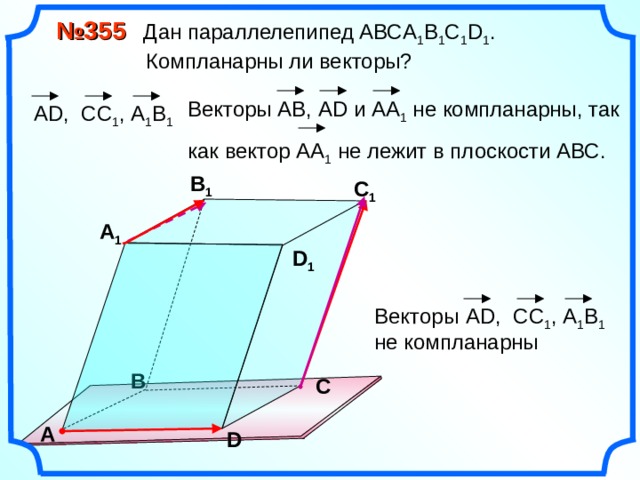
№ 355 Дан параллелепипед АВС A 1 B 1 C 1 D 1 .
Компланарны ли векторы?
Векторы АВ, А D и АА 1 не компланарны, так
как вектор АА 1 не лежит в плоскости АВС.
А D , CC 1 , А 1 B 1
А D , CC 1 , А 1 B 1

Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также компланарны.
Признак компланарности
Если вектор можно разложить по векторам
и , т.е. представить в виде
где x и y – некоторые числа, то векторы , и
компланарны.
c = xa + yb

Справедливо и обратное утверждение.
Признак компланарности
Если векторы , и компланарны, а векторы
и не коллинеарны, то вектор можно
разложить по векторам и
коэффициенты разложения определяются
единственным образом.
Если вектор можно разложить по векторам
и , т.е. представить в виде
где x и y – некоторые числа, то векторы , и
Читайте также:

