Исследование уравнений и неравенств с параметром конспект

Обновлено: 07.07.2024

Если уравнение f x ; a = 0 надо решить относительно переменной \(x\), а буквой \(a\) обозначено произвольное действительное число, то f x ; a = 0 называют уравнением с параметром \(a\).

Решить уравнение с параметром значит найти все значения параметра, при которых уравнение имеет решение.

При разных значениях параметра уравнение может иметь разное число корней или совсем не иметь корней. Также при разных значениях параметра уравнение может решаться по-разному.

Решить неравенство с параметром значит исследовать, каким будет решение неравенства для всех возможных значений параметра.

Развивающая: расширить и углубить изучение различных приемов решения уравнений с параметром.

Воспитательная: показать значимость зависимости ответа в задаче с параметром от выбранного значения параметра.

Используемые методы обучения – их применение.

Объяснительно-иллюстративный.
Обобщения, аналогии и сравнения.
УДЕ – создание ключевых задач, аналогия изображений на плоскости.
Интегрированный – сопоставление алгебры и геометрические интерпретации, слайды.

Формирование общеучебных умений и навыков:

Выделение существенных признаков изучаемых объектов;
Выработка практических навыков;
Используемые методы работы с аудиторией: работа в диалоговом режиме;
Психологические аспекты урока;
Создание комфортной рабочей атмосферы;
Побуждение к активной диалоговой деятельности.

Ход урока

Введение. Вступительное слово учителя.

Уравнения стали привычной частью вариантов вступительных экзаменов ЕГЭ.

Уравнения с параметром вызывают серьезные трудности логического характера.
Каждое такое уравнение – это, по существу, краткая запись семейства уравнений. Ясно, что выписать каждое уравнение из бесконечного семейства невозможно, но тем не менее каждое из них должно быть решено. Поэтому возникает необходимость в рассмотрении системы понятий и поиске методов решения уравнений с параметрами (линейных, рациональных и т.д.)

Поставим задачу: Выяснить, какой может быть ситуация при выбранном значении параметра?

Работа с учащимися в диалоговом режиме.

Обычное линейное уравнение с одной переменной сколько может иметь решений?
Уравнение F(а; х) = 0 что собой представляет?
Как осуществляется его решение?

Итак, при выбранном значении параметра возможна одна из ситуаций;
Уравнение (система):

не имеет смысла;
не имеет корней (решений);
имеет одно, два, три….. корня (решения);
имеет бесконечное множество (решений).

Таким образом, ответ в задаче с параметром существенно зависит от выбранного значения а.

Обозначим основные проблемы:

Установить основные понятия уравнений с параметрами.
Для каждого вида уравнений школьного курса математики установить общий метод решения соответствующих уравнений с параметрами – единый как для одного, так и для двух параметров.
Рассмотреть примеры заданий на исследование уравнений.
Каково установление числа корней уравнений.
Нахождение общего корня двух уравнений – в чем его суть?
Геометрические интерпретации.

I этап – решение первой проблемы.

Работа с учащимися в диалоговом режиме.

Какие вопросы вы себе определите для установления основных понятий?

Что такое задача с параметром?
Что является областью допустимых значений параметра?
Что значит решить задачу с параметром?
Сколько видов задач с параметрами существует?
Что необходимо учитывать при их решении?

Появляется слайд и конспект
- Задача с параметром – это множество задач, каждая из которых получается из условия подстановкой конкретного значения параметра.
- Область допустимых значений параметра – это множество значений параметра, при подстановке которых получается задача, имеющая смысл.
- Решить задачу с параметром означает для любого допустимого значения параметра найти множество всех решений данной задачи.
- Рассматривать мы с вами будем задачи с параметром двух основных типов.
В задачах I типа требуется для каждого значения параметра решить задачу.
Для этого необходимо:

разбить ОДЗ параметра на части, на каждой из которых задачу можно решить одним и тем же способом;
на каждой из полученных частей решить задачу.

1) Решить уравнение а (а – 1) = а – 1.

Делить на ноль нельзя. Придется рассмотреть отдельно случай, когда коэффициент при неизвестном равен о. Получим:

а = 1, тогда уравнение примет вид 0·х = 0, где х – любое число;
а = 0, тогда 0∙х = - 1 – уравнение корней не имеет;
а 0, а 1, тогда а (а – 1)·х = а – 1 х = .

Ответ: 1) если а 0, а 1, то х = ;

2) если а = 1, то х – любое число;

3) если а = 0, то корней нет.

2) Решить уравнение (а – 1)х 2 + 2 (2а – 1)х + 4 а + 3 = 0.

Решение. Рассмотрим два случая:

а = 1 – получим линейное уравнение 2х + 7 = 0, откуда х = - 3,5;
а 1 – получим квадратное уравнение.

Рассмотрим дискриминант: D = (2а – 1) 2 – (а – 1)(4а + 3) = - 3а + 4.

Далее, если а > , то D , то корней нет;

2) если а = 1, то х = - 3,5;

3) если а и а1, то х_1,2 = .

II этап – решение второй проблемы.

Рассмотрим способ классификации частных уравнений с помощью модели общих решений.
Появляется слайд.

Например. В рациональном уравнении функция f₁(а) = является общим решением для тех значений параметра, для которых . Поскольку

общее решение уравнения на А_f1 = >.

Функция f₂(а) = есть общее решение уравнения на множестве А_f2 = .
Построим модель общих решений в следующем виде

На модели выделяем все типы частных уравнений: ; ; .

Итак, на примерах рассмотрены основные понятия уравнений с параметрами: область допустимых значений; область определения; общие решения; контрольные значения параметров; типы частных уравнений.

На базе введенных параметров определим общую схему решения всякого уравнения F(а;х) = 0 с параметром а (для случая двух параметров схема аналогична):

устанавливается область допустимых значений параметра и область определения;
определяются контрольные значения параметра, разбивающие область допустимых значений параметра на области однотипности частных уравнений;
для контрольных значений параметра соответствующие частные уравнения исследуются отдельно;
находятся общие решения х = f₁(а), …, f_k(а) уравнения F(а;х) =0 на соответствующих множествах А_f1, ……, А_fk значений параметра;
составляется модель общих решений, контрольных значений параметра в следующем виде (на слайде);

на модели выделяются промежутки значений параметра с одинаковыми решениями (области однотипности);
для контрольных значений параметра и выделенных областей однотипности записываются характеристики всех типов частных решений.

III этап – примеры заданий на исследование уравнений.

Рассмотрим примеры решения задач с параметрами 2 типа.

1) При каких значениях параметра а уравнение (а 2 + а + 1)х 2 + (2а – 3)х + а – 5 = 0 имеет два корня, один из которых больше 1, а другой меньше 1?

Решение. Пусть f(х) = (а 2 + а + 1)х 2 + (2а – 3)х + а – 5. Так как а 2 + а + 1 >0, то для квадратичной функции f(х) условие задачи может выполняться только при условии f (х) 2 + 4а – 7 2 – 2mх + m + 3 = 0 положительны?

Решение. Пусть f(х) = (m-1)х 2 - 2 mх + m + 3 тогда:

1) если, m = 1,то -2х + 4=0, х= 2- корень положителен;

2) если m 1, то с помощью рисунка можно получить следующие соотношения:

Рассмотрим 2 случая:

1) если 1,5 m > 0, тогда из 2 и 3 неравенств последней системы получим, что m > 1, т.е. окончательно 1,5 m > 1;

2) если m 0 получим, что m-1 2 x – (2а + 9)cosx + 9а = 0 не имеет корней.

Решение. Пусть у = cosх, тогда исходное уравнение примет вид 2у 2 – (2 а + 9)у + 9а = 0, корни которого у₁ = а, у₂ = 4,5. Уравнение cosх = 4,5 корней не имеет, а уравнение cosх = а не имеет корней, если > 1.

Пример 2. Найдите все значения параметра а, при которых уравнение не имеет корней.

Решение. Данное уравнение равносильно системе: .

Уравнение не имеет решения в двух случаях: а = и

Пример 3. При каких значениях параметра а уравнение имеет единственное решение?

Решение. Решение уравнения может быть единственным только, если х = 0. Если х = 0,то а 2 -1 = 0, и а = 1.

Рассмотрим 2 случая:

1) если а = 1, то х 2 - = 0 – корней три;

2). Если а = -1, то то х 2 + = 0, х = 0 - единственный корень.

Пример 4. При каких значениях параметра а уравнение имеет 2 корня?

Решение. Данное уравнение равносильно системе: . Выясним, когда квадратное уравнение х 2 – х – а = 0 имеет 2 неотрицательных корня.

Полученное уравнение имеет два корня, если 1+ 4а > 0; они неотрицательны, если

Во многих случаях при установлении числа корней уравнении имеет значение симметрия.

V этап - нахождение общего корня двух уравнений.

Пример 1. При каких значениях параметра а уравнение х 2 + 3х + 7а -21 =0 и х 2 +6х +5а -6 =0 имеют общий корень?

Решение. Исключим параметр а из полученной системы. Для этого первое уравнение умножим на -5, второе - на7, а результаты сложим. Получим: 2х 2 + 27х +63 =0, корни которого х₁ = -3, х₂ = -10,5. Подставим корни в одно из уравнений и найдем значение параметра а.

Пример 2. При каких значениях параметра а уравнение х 2 – ах + 2 = 0 и 3х 2 + (а - 9)х+ 3=0 равносильны?

Решение. Как известно уравнения равносильны, если множество их корней совпадают. Рассмотрим 2 случая.

1) Уравнения не имеют корней (множество корней пусто). Тогда их дискриминанты отрицательны:

Система неравенств решений не имеет.

2) Уравнения имеют общие корни. Тогда

Следовательно, данные уравнения могут иметь общие корни только при а = 3 или а = .

VI этап – геометрические интерпретации.

Решение задач с параметрами может существенно облегчить использование графиков.

Пример 1. Решите уравнение в зависимости от параметра а: .

Решение. Понятно что при а 0:

Все ли корни подходят. Чтобы это выяснить, построим график функции а =.
Количество корней можно увидеть на рисунке:

Найдем эти корни.

При а = 0 получим х 2 – 2х – 3 = 0 и х₁ = -1, х₂ = 3; при а > 4 это корни уравнения х 2 – 2х – 3 – а = 0.

Если 0 4, то х_1,2 = 1 .

Пример 2. При каких значениях а уравнение имеет более двух корней?

Решение. Если подставить х = 0 в исходное уравнение, то получим 6 = 6, это означает, что х = 0 является решением уравнения при любом а.

Пусть теперь х 0, тогда можно записать . Выясним знаки выражений 2х + 3 и 2х – 3.

Раскроем модули: а = (1)

В плоскости х0а построим множество точек (х;а), координаты которых удовлетворяют соотношению (1).

Если а = 0, то уравнение имеет бесконечное множество решений на промежутке , при других значениях а число решений уравнения не превышает двух.

Тестовый контроль

1 вариант

2 вариант

1) Решите уравнение: 0 · х = а

Ответы: а) при а ≠ 0, х = 1, при а = 0, х R

б) при а = 0, х R, при а ≠ 0 корней нет

в) при а = 0 нет корней, при а ≠ х =

1) Решить уравнение: а х = а.

Ответы: а) при а ≠ 0, х = 1, при а = 0, х R

б) при а = 0, х R, при а ≠ 0 корней нет

в) при а = 0 нет корней, при а ≠ х =

2) Решит уравнение: (в – 2)·х = 5 + в.

а) при в = 2 нет корней; при в ≠2, х = ;

б) при в = -2 нет корней, при в ≠-2 х =

в) при в = -1 нет корней, при а ≠ - 1

2) Решите уравнение (в + 1)·х = 3 – в.

а) при в = 2 нет корней; при в ≠2, х = ;

б) при в = -2 нет корней, при в ≠-2 х =

в) при в = -1 нет корней, при а ≠ - 1

3) При каких значениях параметра с уравнение имеет бесконечное множество решений?

с·(с + 1)·х = с 2 – 1.

Ответ: а) при с = -1, х R,

в) при с = - 1, х R,

3) При каких значениях параметра с уравнение имеет бесконечное множество решений?

(с 2 – 4)·х = (с – 2)·(с+ 1).

Ответ: а) при с = -1, х R,

в) при с = - 1, х R,

4) При каких значениях параметра m уравнения не имеет решений?

Ответы: а) при m = 6 нет корней;

б) при m = 7 нет корней;

в) при m = 8 нет корней.

4) При каких значениях параметра m уравнения не имеет решений?

Ответы: а) при m = 6 нет корней;

б) при m = 7 нет корней;

в) при m = 8 нет корней.

5) Решить уравнение .

а) при а = 0 нет корней, при а ≠ 0 х = ;

б) при а = 0 нет корней, при а ≠ 0 х = ;

в) при а = 0 нет корней, а ≠ 0 х = - 2а.

5) Решить уравнение .

а) при а = 0 нет корней, при а ≠ 0 х = ;

б) при а = 0 нет корней, при а ≠ 0 х = ;

в) при а = 0 нет корней, а ≠ 0 х = - 2а.

6) При каких значениях параметра n уравнение имеет один корень?

nх 2 + 4х + (5 – n) = 0.

а) при n = 0 х =1, при n = 2 х = 2, при n =2 х = ;

б) при n = 0 х = -, при n = 1 х = 2, при n = - 4 х = ;

в) при n= 0 х = - , при n = 1 х = - 2, при n =4 х = - .

6) При каких значениях параметра n уравнение имеет один корень?

nх 2 + 4х + (3 + n) = 0.

а) при n = 0 х =1, при n = 2 х = 2, при n =2 х = ;

б) при n = 0 х = -, при n = 1 х = 2, при n = - 4 х = ;

в) при n= 0 х = - , при n = 1 х = - 2, при n =4 х = - .

Задание:

2. Проверить правильность своего кода с ключом учителя.

Домашнее задание: решить самостоятельно:

1. При каких значениях а уравнение а = имеет более трех корней?

2. При каждом значении параметра а решите уравнение = х – а.

Ответ: если а (- , решений нет

если а [- ] (- 3; 3], то х = ;

3. Сколько корней в зависимости от параметра а имеет уравнение nх = а?

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Уравнения и неравенства с параметрами"

• рассмотреть подробные примеры решения уравнений и неравенств с параметрами.

Мы с вами рассмотрели и решили уже много уравнений, но есть еще один вид уравнений, который часто встречается в алгебре и заслуживает того, чтобы рассмотреть его отдельно. Сначала дадим определение.

Определение.

Особенность таких уравнений состоит в том, что при одних значениях параметра а такое уравнение может не иметь корней, при других – иметь бесконечно много решений. При одних значений – решаться по одним формулам, при других – по другим.

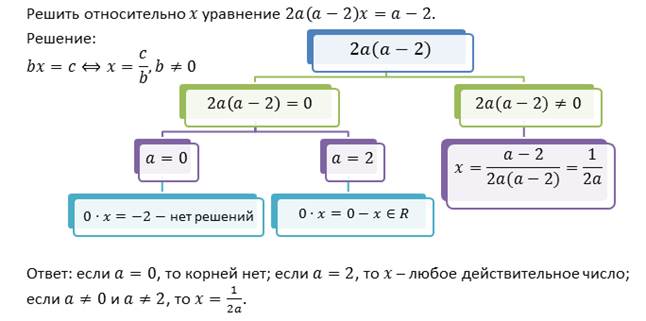
Теперь давайте рассмотрим неравенство с параметрами.

При решении неравенства, необходимо учитывать знак коэффициента перед х. Поэтому к тем случаям, которые мы рассмотрели при решении уравнения добавятся случаи, когда а 2.

Вообще решению уравнений и неравенств с параметрами посвящена масса учебно-методической литературы.

Уравнения вида f (x; y) =0 называется уравнением с двумя переменными.

Уравнение (неравенство) с параметрами – математическое уравнение (неравенство), внешний вид и решение которого зависит от значений одного или нескольких параметров.

Параметр (от греч рarametron – отмеривающий) в математике, величина, числовые значения которой позволяют выделить определенной элемент из множества элементов того же рода.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Вы уже встречались с уравнениями и неравенствами с параметрами. Наша задача обобщить изученный материал.

Уравнения вида f (x; y) =0 называется уравнением с двумя переменными. Решением уравнения с двумя переменными является упорядоченная пара чисел(х;у), при подстановке которой в уравнение f(x;y)=0 оно обращается в верное равенство.

Уравнение х 2 +у 2 =1 имеет бесконечно много решений. Решением является любая пара чисел, лежащая на окружности, R=1.

Изменяем уравнение: х 2 +у 2 =а. Это уравнение с двумя переменными и с параметром а.

При а=0 одно решение х=0, у=0.
При а 0 бесконечно много решений.

Если поставить знак 2 +у 2 2 +В 2 ≠0) есть уравнение прямой

х 2 +у 2 =R 2 (R ≠ 0) есть уравнение окружности

ху=а (а ≠ 0) есть уравнение гиперболы

у=ах 2 +bх+с (а ≠ 0) есть уравнение параболы

Примеры и разбор решения заданий тренировочного модуля

Решение уравнений с параметрами возможно аналитически и графически. Решение уравнений графически позволяет наглядно представить решение.

Задание 1. Сколько решений имеет система?

Построим графики уравнений.

Из рисунка видно, при любом значении а, система будет иметь 2 решения.

Задание 2: Сколько корней в зависимости от параметра а имеет уравнение?

Читайте также: