Формула ньютона лейбница конспект

Обновлено: 16.05.2024

представляю Вам учебный материал по теме "Интеграл. Формула Ньютона - Лейбница".

Вложение	Размер
презентация к уроку	323.62 КБ
конспект урока	65.5 КБ
опорный конспект	35.04 КБ
домашнее задание	24.69 КБ

Предварительный просмотр:

Подписи к слайдам:

Интеграл. Формула Ньютона – Лейбница. составитель: преподаватель математики ГОУНПО ПУ № 27 п. Щельяюр Семяшкина Ирина Васильевна

Цель урока: Ввести понятие интеграла и его вычисление по формуле Ньютона – Лейбница, используя знания о первообразной и правила её вычисления; Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции; Закрепить изученное в ходе выполнения упражнений.

Определение: Пусть дана положительная функция f(x) , определенная на конечном отрезке [ a;b ] . Интегралом от функции f(x) на [ a;b ] называется площадь её криволинейной трапеции. y=f(x) b a 0 x y

Обозначение неопределённого интеграла ввёл Эйлер. Жан Батист Жозеф Фурье Леонард Эйлер Оформление определённого интеграла в привычном нам виде придумал Фурье.

Формула Ньютона - Лейбница

Пример 1. Вычислить определённый интеграл: = Решение:

Пример 2. Вычислите определённые интегралы: 5 9 1

Пример 3 . S y x Вычислить площадь фигуры, ограниченной линиями и осью абсцисс. Для начала найдем точки пересечения оси абсцисс с графиком функции . Для этого решим уравнение. = Решение: S =

y x S A B D C Пример 4 . Вычислить площадь фигуры, ограниченной линиями и Найдём точки пересечения (абсциссы) этих линий, решив уравнение S=S BADC - S BAC S BADC = = S BAC = S = 9 – 4,5 = 4,5 смотри пример 1 Решение:

ПРАВИЛА СИНКВЕЙНА 1строка – тема синквейна 1 слово 2строка – 2 прилагательных, описывающих признаки и свойства темы 3строка – 3 глагола описывающие характер действия 4строка – короткое предложение из 4 слов, показывающее Ваше личное отношение к теме 5строка – 1 слово, синоним или Ваша ассоциация тема предмета.

Интеграл 2. Определённый, положительный Считают, прибавляют, умножают 4. Вычисляют формулой Ньютона - Лейбница 5. Площадь

Список используемой литературы : учебник Колмагорова А.Н. и др. Алгебра и начала анализа 10 - 11 кл .

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

ОГБПОУ СОТА

Осипян К.В., преподаватель ОГБПОУ СОТА

Образовательная - сформировать понятие определенного интеграла, отработать навыки вычисления определенного интеграла; ввести формулу Ньютона-Лейбница, рассмотреть свойства определенного интеграла.

Развивающая - создать условия для развития мышления (умения строить аналогии, систематизировать и обобщать), развить познавательный интерес.

Воспитательная - воспитать осознанное отношение к учебной деятельности.

Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись

Как видно на графиках (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F(b) - F(a)).

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.

Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,

Это равенство называется формулой Ньютона-Лейбница.

Разность F(b) – F(a) кратко записывают так:

Поэтому формулу Ньютона-Лейбница будем записывать и так:

Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b, далее - значение нижнего предела a и вычисляется разность F(b) - F(a). Полученное число и будет определённым интегралом.

При a = b по определению принимается

Свойство 1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю , т.е.

Свойство 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.

Свойство 3. Постоянный множитель можно выносить за знак определённого интеграла , т.е.

Свойство 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.

Свойство 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется (т.е. по модулю), а изменяется лишь его знак , т.е.

Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.

Вычислить определенный интеграл

Решение:

Вычислить определенный интеграл

)

Задание для самостоятельного решения:

1. Вычислите интеграл .

2. Вычислите интеграл .

3. Вычислите интеграл .

4. Вычислите интеграл .

5. Вычислите интеграл .

6. Вычислите интеграл .

7. Вычислить интеграл

8. Вычислить интеграл

На этом уроке показывается геометрический и физический смысл определенного интеграла. Рассказывается история интегрального исчисления. Вводится формула Ньютона-Лейбница.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Определенный интеграл. Формула Ньютона-Лейбница"

• показать геометрический смысл определённого интеграла;

• показать физический смысл определённого интеграла;

• рассказать историю интегрального исчисления;

• ввести формулу Ньютона-Лейбница.

Давайте рассмотрим задачу.

Пусть в декартовой прямоугольной системе координат дана фигура:

Такую фигуру мы назовем криволинейной трапецией. Требуется вычислить площадь криволинейной трапеции.

Рассмотрим еще одну задачу.

Пусть дан прямолинейный неоднородный стержень.

Нам надо найти массу стержня.

Рассмотрим еще одну задачу.

Пусть по прямой неравномерно движется материальная точка. Зависимость скорости от времени выражается формулой v = v(t). Надо найти перемещение точки за промежуток времени [a; b].

Итак, при решении каждой задачи, мы получали одну и ту же математическую модель. Задач, которые приводятся к этой же математической модели довольно много. Поэтому возникла необходимость специально изучить данную математическую модель, то есть присвоить ей новый термин, ввести для нее обозначение, научится с ней работать.

Давайте еще раз дадим математическое описание той модели, которую мы использовали в задачах:

В курсе математического анализа доказано, что этот предел в случае непрерывной (или кусочно-непрерывной) функции существует. Его обозначают так

Числа a и b называют пределами интегрирования (соответственно верхним и нижним). Здесь dx – замена Δx, длин кусочков из которых состоит целое.

Согласно интернет энциклопедии Википедии интегрирование прослеживалось еще в Древнем Египте, примерно в 1800 году до нашей эры. Первым известным методом для расчета интегралов является метод исчерпывания Евдокса, который пытался найти площади и объемы, разрывая их на бесконечное множество частей, для которых площадь или объем уже известны. Это метод был подхвачен и развит Архимедом. Аналогичные методы были разработаны независимо в Китае в третьем веке нашей эры.

Следующий значительный прогресс в исчислении интегралов появился в шестнадцатом веке. В работах Кавальери с его методом неделимых, а также в работах Ферма, были заложены основы современного интегрального исчисления. Дальнейшие шаги были сделаны в начале семнадцатого века Барроу и Торичелли, которые представили первые намеки на связь между интегрированием и дифференцированием.

В качестве символа интегрирования, Ньютон использовал значок квадрата перед обозначением функции или вокруг него, но эти обозначения не получили широкого распространения. Современное обозначение было введено Лейбницем в 1675 году. Он образовал интегральный символ из длинной буквы S – сокращения латинского слова сумма. Современное обозначение определенного интеграла, с указанием пределов интегрирования, были впервые предложены Жаном Батистом Жозефом Фурье в 1820.

Введя понятие определенного интеграла, мы можем переписать формулы, полученные при решении наших задач.

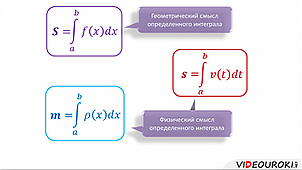
Площадь криволинейной трапеции можно найти так:

В этом состоит геометрический смысл определенного интеграла.

Определение массы прямолинейного неоднородного стержня с плотностью ро от икс можно вычислить так:

В этом заключается физический смысл определенного интеграла.

Определение перемещения материальной точки, движущейся по прямой со скоростью v(t), за промежуток времени [a; b] можно записать так:

Это еще одно физическое истолкование определенного интеграла.

Давайте еще раз вернемся к третьей задаче.

Мы записали, что перемещение точки, которая движется со скоростью v(t), за промежуток времени [a; b] вычисляется по формуле:

С другой стороны, координата движущейся точки – это первообразная для скорости:

В курсе математического анализа доказана следующая теорема:

Поэтому эту формулу называют формулой Ньютона – Лейбница. На практике вместо разности пишут так:

ТЕМА ЗАНЯТИЯ: Определенный интеграл и его свойства. Формула Ньютона-Лейбница.

ЦЕЛИ И ЗАДАЧИ: 1. Образовательные:

а) закрепить навыки нахождения определенного интеграла;

б) обеспечить усвоение студентами понятия определенный интеграл и различных способов нахождения определенного интеграла;

в) отработать навыки нахождения определенного интеграла.

2. Развивающие:

а) развитие психических качеств студентов (умений применять полученные знания на практике);

б) развитие познавательных умений и мышления (выделять главное, анализировать, сравнивать, определять и объяснять понятия).

3. Воспитательные:

а) воспитание положительного отношения к знаниям;

б) воспитание дисциплинированности;

в) воспитание эстетических взглядов.

ТИП ЗАНЯТИЯ: Изучение нового материала

МЕТОДЫ ОБУЧЕНИЯ: объяснительно-иллюстративный, практический

ИНФОРМАЦИОННО- МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ:

Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних профессиональных заведений – М.: Высшая школа. 2008, стр 205-208
Богомолов Н.В., Самойленко П.И. Математика. Среднее профессиональное образование, -М.: Дрофа,2010 стр 271-273

ПЛАН ЗАНЯТИЯ:

Введение 5 мин
Повторение пройденного материала 10 мин
Объяснение нового материала 20 мин
Закрепление пройденного материала 30 мин
Самостоятельное решение 15 мин
Проверка самостоятельной работы 5 мин
Подведение итогов 5 мин

ПЛАН ЗАНЯТИЯ № 11